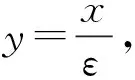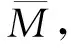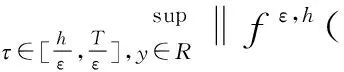波尔兹曼方程到欧拉方程黎曼解的流体动力学极限
黄飞敏
(中国科学院 数学与系统科学研究院, 北京 100190)
0 引 言
作为统计力学中的基本方程, 波尔兹曼方程有以下形式
(1)
其中,f(t,x,ξ)表示粒子在位置x和时间t具有速度ξ的分布, 这里Knudsen数ε>0与粒子的自由平均程成正比.
众所周知,波尔兹曼方程[1]与宏观的流体力学方程,如欧拉方程、纳维-斯托克斯方程紧密相关.早在麦克斯韦尔和波尔兹曼时代, 人们就意识到了这些联系.1912年希尔伯特提出了著名的希尔伯特展开,Enskog和Chapman分别在1916年和1917年相互独立地提出了另外一种展开(后称之为Enskog-Chapman展开).根据Knudsen数ε,希尔伯特展开和Enskog-Chapman展开均得到主要近似为可压缩欧拉方程, 之后的项为可压缩纳维-斯托克斯方程.注意到以上只是形式展开, 严格的数学证明一直未得到解决, 部分原因是欧拉方程自身的适定性理论没有得到解决.事实上,波尔兹曼方程的流体动力学极限与著名的希尔伯特第六问题密切相关.
本文简要回顾了关于波尔兹曼方程流体动力学极限的研究工作.当欧拉方程具有光滑解时,波尔兹曼方程的流体动力学极限已有比较丰富的工作, 见Caflisch[2], Lachowicz等[3], Nishida[4]及Ukai等[5].但即使初值充分光滑, 欧拉方程的解通常会在有限时间内产生奇性, 比如激波和接触间断波[6], 因此,在奇异解情形下研究波尔兹曼方程的流体动力学极限是有意义的. 黎曼解是研究一般奇异解的基石, 最早由黎曼在1860年开始研究.黎曼当时研究了一维等熵气体动力学方程组, 初值由2片常数组成, 由原点分开.这样的初值后称为黎曼初值, 对应的解称为黎曼解.它不仅能捕获解的局部和整体行为, 并且完全反映了非线性项的影响. 对于欧拉方程, 黎曼解包含三类基本波, 即激波、稀疏波和接触间断波.所谓的黎曼解由这三类基本波线性叠加而成.注意到这三类基本波拥有完全不同的性质, 即激波具有压缩性, 稀疏波具有膨胀性, 接触间断波具有扩散结构.对这些基本波的研究完全依赖于波的基本性质, 因此,在由这些具有不同性质的基本波组成黎曼解的情形下, 从数学上严格验证波尔兹曼方程的流体动力学极限是一个具有很大挑战性的难题.
根据这些基本波的特有性质,单个基本波的流体动力学极限已被严格证明了, 如激波[7]、稀疏波[8]和接触间断波[9].由于以前研究这些基本波的方法严重依赖于波的特有性质且互不兼容, 因此,波的叠加情形仍然是一个具有挑战性的公开问题.在文献[10-11]中,笔者分别证明了稀疏波+接触间断波和激波+稀疏波叠加的情形.在文献[1]中,利用研究激波的方法来统一研究三种基本波的叠加情形, 付出的代价就是稀疏波和接触间断波引起的误差太大.为此引入了二类双曲波分别克服稀疏波和接触间断波产生的困难.利用以上想法、精细的先验估计及尺度变换方法,笔者在文献[1]中对于一般黎曼解情形, 严格证明了波尔兹曼方程的流体动力学极限,并得到了关于Knudsen数ε的收敛速率.
1 波尔兹曼方程
考虑如下波尔兹曼方程
(2)
其中,ξ=(ξ1,ξ2,ξ3)∈R3,x∈R,Q(f,g)为碰撞算子.笔者主要考虑硬球碰撞模型.同样方法也可以应用到硬位势模型.当ε趋于0时, 波尔兹曼方程(2)形式上收敛到以下可压缩欧拉方程:
(3)
其中,
(4)
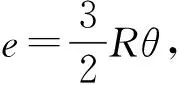
(5)
满足
作如下微观-宏观分解[12-14],即
f(t,x,ξ)=M(t,x,ξ)+G(t,x,ξ),
其中,
M=M[ρ,u,θ](t,x,ξ)=
(6)
为局部麦克斯韦分布,G(t,x,ξ)表示微观量.
由于在一维空间使用拉格朗日坐标更方便, 作如下坐标变换, 即
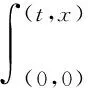
(7)
仍记坐标参数为(t,x), 这样方程(2)和(3)在拉格朗日坐标里分别变为
(8)
以及
(9)
2 黎曼问题
现在回顾欧拉方程组(9)的黎曼问题,即考虑初值
其中,u±=(u1±,0,0),v±,θ±>0为常数.众所周知,以上黎曼问题包含了三种不同传播速度的基本波, 即激波、稀疏波和接触间断波, 见文献[6].给定右状态(v+,u1+,θ+), 以下为相平面上关于左状态(v,u1,θ)的曲线:
★接触间断波曲线:
CD(v+,u1+,θ+)={(v,u1,θ)│u1=u1+,
p=p+,v≠v+}
(10)
★i-稀疏波曲线i=1,3:
Ri(v+,u1+,θ+)={(v,u1,θ)│v (11) 其中,s=s(v+,θ+),i为方程组(9)的第i-族特征速度; ★i-激波曲线i=1,3: (12) (13) (14) 由于稀疏波在t=0具有奇性, 因此,在区间[h,T]上考虑波尔兹曼方程解的流体动力学极限, 其中,h>0为任意小常数,T>0为固定的任意常数. 其中, 区域Σh,T={(t,x)│h≤t≤T,|x-s3t|≥h}, 常数Ch,T不依赖ε. 注由于以1-稀疏波、2-接触间断波和3-激波组成的解为黎曼解的典型情形, 定理1也适用于黎曼解的其他情形. 引入以下尺度变换 (15) 由于1-稀疏波、2-接触间断波和3-激波均为可压缩欧拉方程组(9)的奇异解,正则性不高,则需要构造光滑的逼近稀疏波(VR1,UR1,ΘR1)、逼近接触间断波(VCD,UCD,ΘCD)和行波解(VS3,US3,ΘS3)[15]来代替相应的稀疏波、接触间断波和激波.又由于利用了研究激波的方法来统一研究波的叠加情形, 付出的代价就是由稀疏波和接触间断波引起的误差太大.为了克服这些困难,引入二类双曲波来分别克服稀疏波和接触间断波产生的困难,见文献[1].设(V,U,E)为由这5种波组成的逼近复合波.围绕逼近复合波, 定义以下扰动量 (16) 其中,行波解Fs3=M[VS3,US3,ΘS3]+Gs3.根据以上尺度变换, 波尔兹曼方程的流体动力学极限问题可以转化为波尔兹曼方程的长时间稳定性问题.特别是选择零初值,即 (17) 以下是关键的先验估计: (18) 注意到式(18)的收敛速率比定理1中的收敛速率要快,本文得到了理想的先验估计,即定理2.再结合局部存在性定理,成功证明了定理1, 见文献[1].

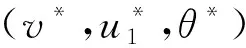
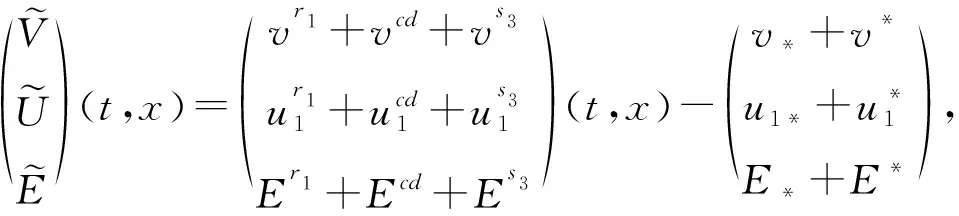
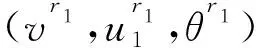
3 主要定理
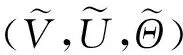
4 思 路