尺规作图连接两距离过远的点的方法

于悦海 周 正 李晗菲 于茗雅 李佳恒

(北京一零一中学初三7班 100091)

数学课上我们碰到了这样的问题：

问题黑板上两个点A，B，距离大于直尺或三角板的最长边，如何用尺规作图把A，B两点用直线连起来？

首先，我们需要确定几种位置关系的作法：

引理1 任两点连线段的垂直平分线(中点)

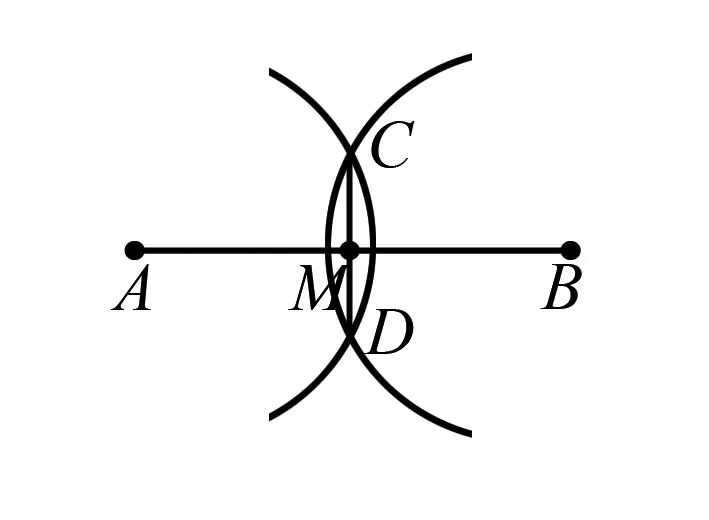
图1

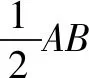
引理2 作任一角的平分线

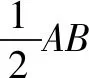
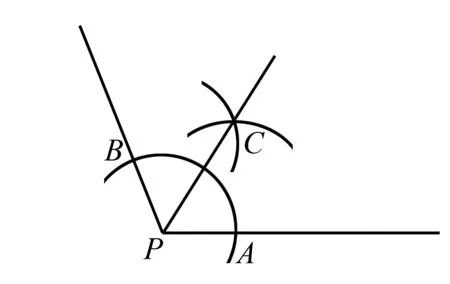
图2

特别地，作180°角的角平分线即过角的顶点作角两边所在直线的垂线．(留给读者一个问题，如何过直线l外一点作直线l的垂线？如果这点与直线的距离大于圆规的最大半径呢？)

引理3 过直线l外一点P作直线l的平行线

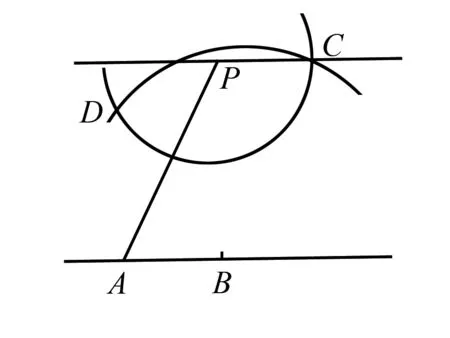
图3

如图3，在直线上任意取A，B两点，以B为圆心，AP长为半径画弧，以P为圆心，AB长为半径画弧，两弧交于点C、D，连接PC，PC即为所求的直线的平行线．如果这点与直线的距离大于圆规的最大半径，则可重复此作法作与点P距离较小的平行线，直至尺规足够作出已知直线的平行线的过点P的平行线．

下面给出三种尺规作法和一种近似作法：

作法1中心对称法

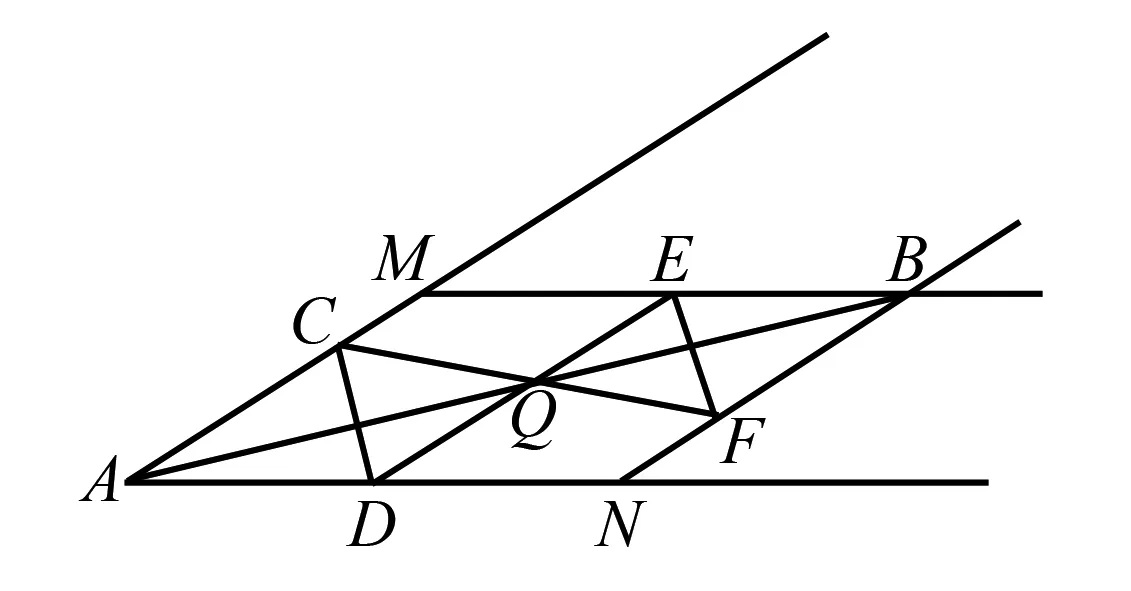
图4

如图4，过点A作两条射线使得两条射线都足够接近点B并且点B在两条射线之间(如何作到尽量接近？)，借助引理3，过点B作这两条线的平行线，得到平行四边形AMBN．在四条射线取四个点C，D，E，F使得AC=AD=BE=BF(使C，D，E，F的距离尽量小，以至用尺子或圆规可以够到)．连接CD，EF．容易看出△CAD≅△FBE．

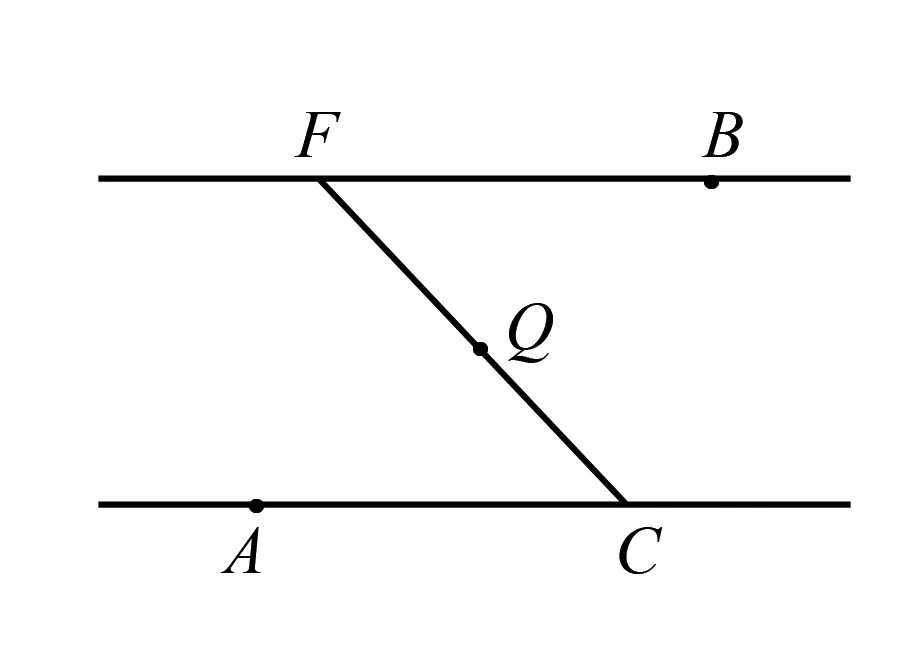
图5

易证，△CAD与△FBE关于AB的中点Q成中心对称，于是连接对应点CF，DE，交点即为对称中心Q(成中心对称的两个图形对应点连线段一定经过对称中心且被对称中心平分)．于是问题转化为连AQ，BQ.若AQ距离依然过大以至于无法连接，即重复上面的方法即可．

所需工具：引理3，中心对称的性质，平行四边形的判定及性质．

类似作法：如图5，只作一组平行线AC，BF，截取AC=BF，连CF，CF的中点Q即为AB的中点．这样需要再借助引理1．

作法2矩形对角线法

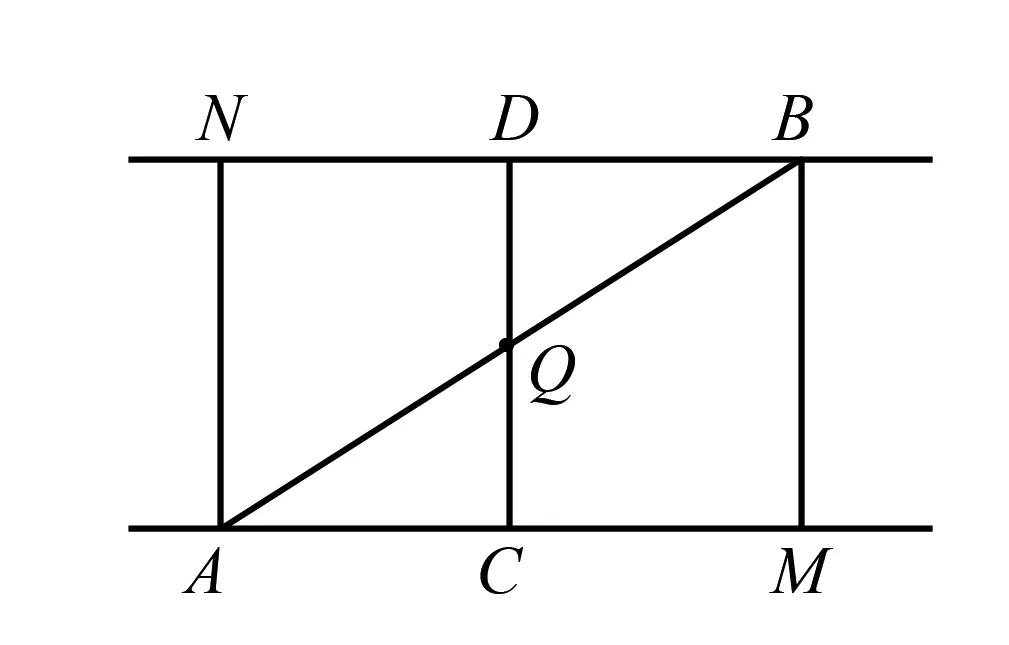
图6

如图6，过A作一条射线AM尽量接近B，利用平行线的作法作出过B的这条线的平行线BN，借助引理2过A作BN的垂线，过B作AM的垂线．此时四边形AMBN为矩形(有三个角都是90°)．借助引理1作AM，BN的中点C，D并连接CD．作CD的中点Q，分别连接AQ，BQ即可．(证明Q为矩形对角线方法的过程见图7)

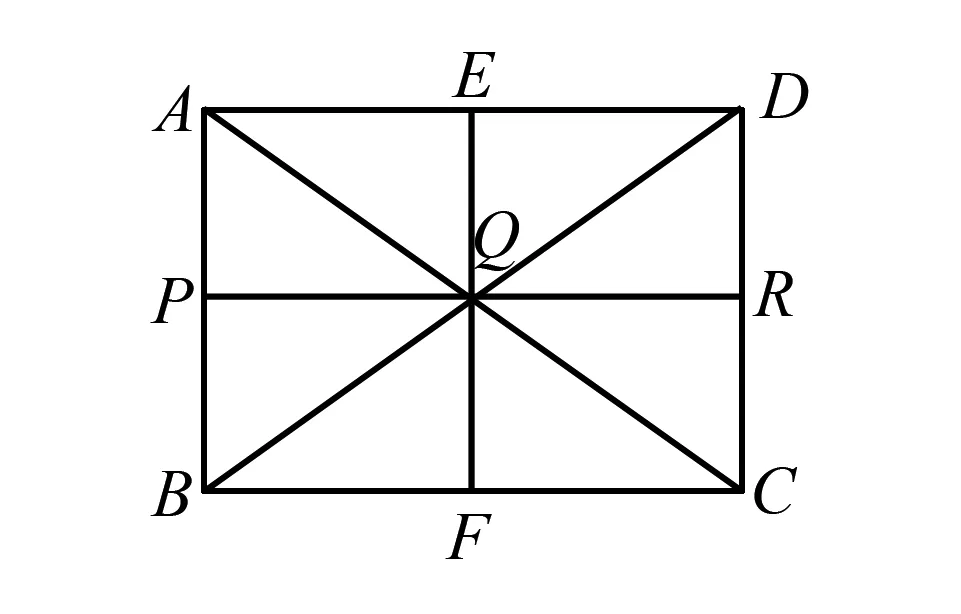
图7

如图，M、N分别是AD，BC中点，Q是MN中点

证Q是矩形ABCD对角线交点

过Q作PR∥AD，交AB于P，DC于R.

∴四边形AMPQ，DMQR，BNQP，CNQR都是矩形

∴MQ=NQ=AP=BP=DR=CR

∴PR垂直平分AB，CD.

∴AQ=BQ=CQ=DQ

设∠AOB为x,∠COB为y

则∠ACD=∠CDB=y,∠CAD=∠AOB=x

∵x+y=90°

∴2x+2y=180°

∴(180°-2x)+(180°-2y)=180°

即∠AQC=180°

∴Q在AC上，同理Q也在BD上

∴Q在对角线交点上

所需工具：引理3，矩形判定及性质，引理1．

作法3中位线法

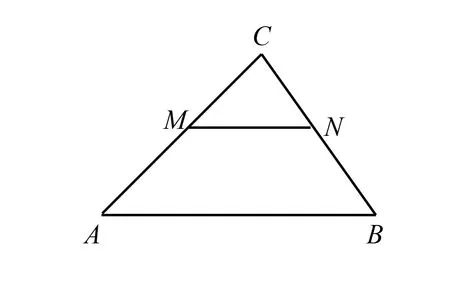
图8

如图8，分别过A，B作两条射线，两条射线交于C，由引理1作AC，BC中点，记为M，N，连接MN，则MN是三角形ABC〗的中位线，此时只需由引理3过B作MN的平行线并延长即可连接AB．(留给读者一个问题，如果M，N距离大到无法连接呢？)

所需工具：引理1，中位线定理，引理3．

作法4一次函数近似作图法(不属于尺规作图)

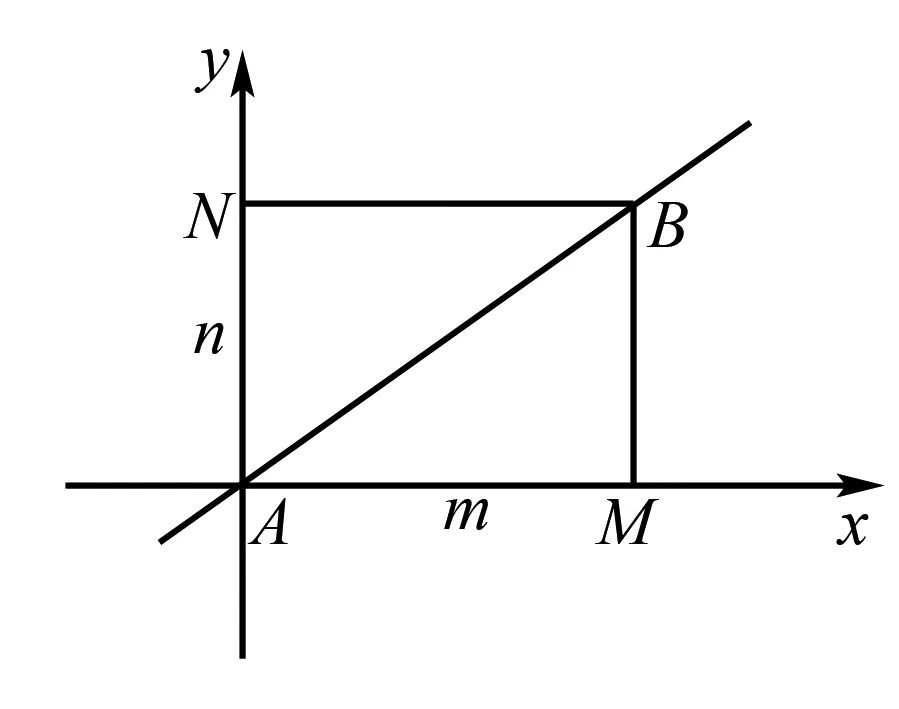
图9

如图9，以点A为原点建立坐标系，由引理2，过点B分别向x轴，y轴作垂线，点B的坐标可在坐标轴上近似读出为(m，n)．将(m，n)代入一次函数解析式y=kx，将一次函数(正比例)解析式求出，画出一次函数图象即可．

所需工具：引理2，一次函数．