Sketchpad在微课应用中的案例与研究

张 磊

(江苏省徐州市第二中学 221005)

一、引言

历年江苏高考对解析几何部分知识考查主要是关于“直线和圆”两个C级考点的基础知识与基本技能.本文是在2018年9月高三一轮复习时讲授江苏高考题时的课堂案例实录.因题中涉及的点、线、圆以及向量的数量积不够直观，涉及到的不等关系较为复杂，学生直接解答并不容易.所以，我就利用Sketchpad软件直观地构造出较为复杂的数学图形和动画，通过对其变换、度量、计算和跟踪生成轨迹等方式，为教师和学生提供一个讨论“直线与圆”问题内在关系的教学案例.

二、试题回顾

解析及Sketchpad辅助设计指导本题所求是满足条件的点P的横坐标取值范围，我们可以构造关于其的不等关系进行求解.

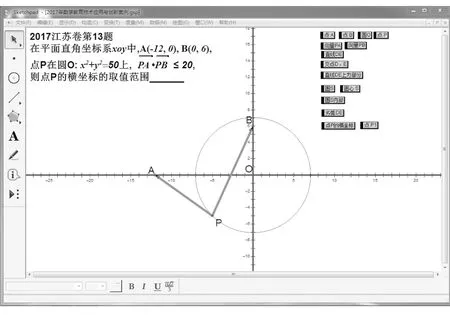
图1

图2

联立圆S:(x+6)2+(y-3)2=65与圆O:x2+y2=50.

图3

图4

图5

本例主要考查了直线与圆(圆与圆)的相交问题，是解析几何中常见题目.而问题中探求点的轨迹更是平面解析几何研究的重要问题之一，也是高中生难以理解和掌握的内容.传统教学中，学生只能手工画出动点轨迹的草图或在头脑中简单地想象，轨迹的精准性、完备性往往难以把握，手工画图常使学生、教师在解题时，考虑得不够完整全面，遗漏了动点的特殊位置以及动点运动的多种情形，从而造成轨迹的遗漏和不完整.借助Sketchpad，可以直观、动态地描绘出运动轨迹的形成过程，帮助学生认识轨迹的本质特征，有助于学生从中获得解决问题方法.该案例从题干给出得相关方程出发，准确地画出其对应的图形，突出了Sketchpad较之其他数学软件最大的优势——几何图形的动态化、“形”与“数”的同步化和操作的简单直观化.

笔者在平面解析几何课程教学过程中，借助微课平台，利用Sketchpad的优势和高三同学的认知特点，有针对性地设计了大量的微课视频，并借助这些教学案例所创设的问题情境展开教学活动，充分调动了学生在操作中观察、在探索中思考、在合作中交流，不仅点燃了学生的学习热情，而且克服了传统教学中的不足，有效地促进了学习活动的开展.这些案例讨论Sketchpad在平面解析几何教学中数学概念的形成、数学定理的发现与验证、数学问题解决过程中的应用一窥，值得借鉴.