储能变流器直流电池电流控制研究

王伟岸

上海电气集团股份有限公司 输配电分公司 上海 200042

1 研究背景

储能技术可以弥补新能源发电的随机性与波动性,使大规模风电及太阳能发电安全可靠并入电网。同时可以缓解电力系统由于发电、用电不平衡所引起的巨大峰谷差,实现电力的削峰填谷。储能技术还可以促进微电网的应用,提高供电可靠性。

储能变流器是储能系统中的关键设备,是储能介质和电力系统间的纽带,同时也是实现多样化储能系统应用的执行部件。现阶段,全球已实现商用或示范应用的电化学储能介质主要有铅酸电池、铅碳电池、锂电池、液流电池等。受限于产品特性与制造水平,现有储能电池对充放电电流的倍率和电流波动有一定要求,过大的电流波动和电流峰值不仅会缩短电池的使用寿命,而且会危及整个储能系统的安全。当电网负载不对称或发生不对称故障时,会出现三相不平衡电压,从而会使储能变流器直流侧电池功率、交流侧电网功率出现二倍频波动。由于直流电池电压在短时间内基本恒定,因此二倍频功率波动在电池侧表现为充放电电流的波动。该波动电流可能使功率超出电池允许的最大瞬时输出功率,将导致所需储能电池的容量增加或电池的使用成本提高。

为改善电压不对称情况下的直流功率波动,可以在储能变流器的直流侧增加储能电容,在直流母线上串接平波电抗器[1-2],或者采用两级式储能变流器结构,在直流母线与储能电池之间增加一级直流变换器,但以上做法不仅会降低整个系统的效率,而且会大大增加系统成本。

笔者分析了三相电压不平衡时储能变流器出现二倍频功率波动的原因,建立了储能变流器电压电流双闭环正负序控制数学模型,在研究传统并网变流器控制策略的基础上[3-4],通过改变储能变流器的电流内环给定值,来抑制直流电池的功率及电流波动,并通过仿真结果证明了所提方法的有效性。

2 储能变流器数学模型

中点钳位型三电平变换器是目前应用广泛的储能变流器,具有如下优点:① 每个功率管承受的电压是直流母线总电压的1/2,允许提高开关管的工作频率,并且损耗低;② 相同的开关频率下,输出波形为三电平叠加,从而使输出波形的谐波含量低;③ 电容中点的引出可以为系统提供中线输出能力,方便用于三相四线制电力系统。中点钳位型三电平变换器结构如图1所示。

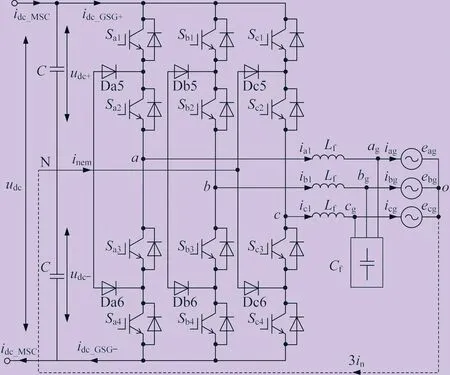
图1 中点钳位型三电平变换器结构

选取输入变量为三相输入电压eag、ebg、ecg,状态变量为交流侧三相电流iag、ibg、icg,忽略三相交流滤波电容电流,并忽略直流侧上下电容电压波动,根据基尔霍夫电压定律方程和基尔霍夫电流定律,建立储能变流器的数学模型[5-10]:

(1)

式中:S1a、S1b、S1c、S2a、S2b、S2c为三相开关函数;Lf、Rf分别为交流滤波电感的电抗和电阻;uno为储能变流器直流电容中点与电网电压中性点间的电压,当采用三相四线制时,uno为0;t为时间。

在三相静止坐标系下,三相电压、电流都是交流量,是时刻变化的,不利于设计控制系统,而同步旋转坐标系下的变量都是直流量,是保持不变的,便于设计采用比例积分控制原理的控制系统。通过坐标变换,将原储能变流器数字模型变换为同步旋转坐标系下数学模型:

(2)

式中:ud、uq分别为储能变流器输出电压的d轴、q轴分量;idg、iqg分别为d轴、q轴下的输出电流;ω为电网电压角频率。

当电网电压三相不平衡时,如要分序控制储能变流器,则式(2)数学模型需要变换到正序、负序复矢量下,此时复矢量数字模型为:

(3)

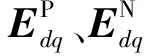
3 不平衡分量提取

以三相电流为例说明不平衡分量的提取方法。在三相三线制系统中,假设交流电流中仅含有基波的正序、负序分量,则在静止坐标系下,三相电流可表示为:

(4)

式中:ω为电流的旋转角频率;Ip、In分别为电流正序、负序分量的幅值;φp、φn分别为负载电流正序、负序分量对应的初相位。

将三相电流从三相静止坐标系变换到两相静止坐标系,应用坐标变换:

(5)

将式(4)代入式(5),可以在两相静止坐标系下将电流的α轴、β轴瞬时值分量用正序、负序分量表示:

(6)

式中:ipα、ipβ、inα、inβ为负载电流正序、负序分量对应在两相静止坐标系α轴、β轴上的分量。

对式(6)中的ωt作微分运算,可得:

(7)

两相静止坐标系下电流瞬时值的微分值可以通过离散数字量计算来得到:

(8)

式中:Δt为计算步长,可采用数字信号处理算法中的中断时间;iα(t)、iα(t-Δt)、iβ(t)、iβ(t-Δt)为两相静止坐标系下本次采样时刻和上一次采样时刻的电流瞬时值。

联立式(6)、式(7),可得:

(9)

通过适当的线性运算,得到两相静止坐标系下的电流正序、负序分量,再经过一级旋转坐标变换,即可变换至相应的同步旋转坐标系下。

4 储能变流器直流控制策略

三相不对称下,储能变流器的输出复功率S为:

(10)

分解有功功率p和无功功率q:

(11)

整理式(10)与式(11),可以得到各功率分量幅值的表达式:

(12)

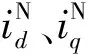
(13)

可以看出,除了恒定的直流功率p0外,还存在功率波动p1、p2。波动幅值的大小与三相电压不平衡度有关,三相电压越不平衡,直流功率波动量也就越大。在电网电压恶劣的情况下,传统的并网变流器控制方法无法满足电池的恒电流或恒功率精度要求。

选取式(12)中的前四个方程作为约束条件,并简化为:

(14)

如储能变流器的目标为控制直流电流或直流功率恒定,则令p1=p2=0,解得:

(15)

此时在储能变流器的控制中,采用正序、负序分离的方法,可以分别控制整流器发出给定的正序、负序电流。系统控制框图如图2所示。

5 仿真分析

为了验证正负序提取方法的有效性,应用MATLAB/Simulink仿真软件进行仿真研究。

仿真时,交流电网额定电压为380 V,储能变流器三相交流滤波电感为0.6 mH,三相交流滤波电容为40μF,储能变流器采用三电平结构,直流侧上下支撑电容分别为20 mF,正负直流母线直接连接至储能电池,电池电压工作范围为650～800 V,开关频率为10 kHz,采用三相正弦脉冲宽度调制方法。

仿真过程中,0 s开始三相电网电压平衡,在0.05 s时启动储能变流器,设定储能系统输出有功功率100 kW,从0.1 s开始电网电压出现三相不平衡,其中A相电压升高20%,B相、C相电压保持不变。

仿真结果如图3所示。由于三相电压不平衡的影响,利用传统方法控制储能变流器后,直流电池电流将出现电流的二倍频波动,电流波动峰峰值约为70 A。采用直流电流控制策略后,在同样的电网不平衡条件下,直流电池电流峰峰值可以控制在20 A以内。

为了验证方法的有效性,再对B相、C相电压升高、A相电压降低的不平衡工况进行仿真,仿真结果如图4所示。同样可以看出,采用直流电流控制策略后,直流电池电流的波动大幅降低,有利于储能电池的安全长寿命运行。

图3 单相电压升高时仿真结果`

图4 两相电压升高时仿真结果

6 结束语

通过建立储能变流器正负序控制数学模型,分析三相电压不平衡下产生直流电流波动的原因,并从抑制直流电流波动角度应用储能变流器直流电流控制策略,进而大大抑制储能电池电流和功率波动。虽然这一方法并不能完全将直流电流波动消除,但是这一方法简便且容易实现,可以满足实际工程上的需要。通过仿真验证了这一方法的有效性。