送粉管道联合吊架拉杆的设计

王 源, 温 泉

1.上海电气电站工程公司 上海 201100 2.中国能源建设集团 安徽省电力设计院有限公司 合肥 230601

1 设计背景

在国家持续降低供电煤耗和提高环保标准的背景下,火力发电厂不断向高参数、大容量发展[1]。《煤电节能减排升级与改造行动计划(2014—2020年)》中明确指出,新建燃煤发电项目原则上采用600 MW及以上超超临界机组。

大型火力发电厂锅炉燃烧器的数量较多,导致煤粉管道数量也较多。一般情况下,四角切圆煤粉炉共有24根煤粉管道,前后墙对冲煤粉炉共有36根煤粉管道。在煤粉管道的布置设计中,往往会出现多根管道联合支吊的情况。

在以往的工程设计中,联合吊架拉杆应力分析均按照《火力发电厂烟风煤粉管道设计技术规程》中的静力矩平衡法进行计算[2]。以三拉杆联合吊架为例,按规程进行载荷分配后,中间一根拉杆承受1/2载荷,两边各承受1/4载荷,最后整体按1/2载荷选型。这样的吊架设计缺乏精确性和严谨性,难以适应火电厂精细化设计的发展趋势[3-4]。

笔者建立吊架模型,根据模型的约束特点,采用结构力学中的位移法对大型送粉管道联合吊架拉杆的受力情况进行分析,给出受力方程,并对拉杆选型进行合理优化,节省投资。

2 送粉管道布置方案

某2×660 MW火电厂采用侧煤仓布置,锅炉为前后墙对冲燃烧、二次再热、Π型锅炉,每墙布置三层燃烧器,标高依次为+23.225 6 m、+28.613 6 m、+34.001 6 m,每层有六台旋流煤粉燃烧器。制粉采用中速直吹式系统,单炉配备六台磨煤机,每台磨煤机对应六根送粉管道,连接每层的燃烧器。

送粉管道管径为508 mm,设计压力为21.68 kPa,防爆设计压力为0.4 MPa,设计温度为110 ℃。典型的联合吊架设置形式如图1所示。图1中,1为联合吊架的管道支撑梁,2为联合吊架生根的构筑梁,A、B、C为联合吊架的三根拉杆,负责将联合吊架固定在构筑梁上,P1～P6为支撑在联合吊架上的六根送粉管道。

图1 联合吊架设置形式

这一工程存在大量六根送粉管道联合支吊的情况,采用三拉杆联合吊架后,每根拉杆的受力在材料力学上属于超静定问题,以往不对此类问题进行分析研究,导致吊架选型不合理。笔者以此类三拉杆联合吊架为例进行分析。

3 联合吊架拉杆受力分析

3.1 受力分析方法

当吊架组件所受应力的值达到或超过材料强度极限时,材料可能产生开裂、变形、断裂、失稳等现象[5-6],将导致吊架失效或被破坏。而若盲目选择高规格的吊架组件,则会造成建设资金的浪费。联合吊架拉杆受力分析的目的是对吊架超静定受力工况进行力学分析,使吊架组件在设计要求的载荷作用下,有效抵抗不被允许的变形和破坏,在保证管道和吊架安全性的同时,兼顾经济性的需求。

超静定结构体系的内力计算方法依据静力平衡条件和变形协调条件,可分为两大类:力法和位移法[7-8]。力法以力为基本未知量,释放关键点的约束,以未知力表示关键点的位移,根据变形协调条件,求出关键点的未知力,从而求出整个结构的内力。位移法以位移为基本未知量,约束关键点,依据变形协调条件,以未知位移表示关键点的力,再根据关键点的静力平衡条件,求出关键点的位移,从而求出整个结构的内力[9]。

力法出现得较早,只用于计算超静定结构。位移法出现得稍晚,适用于静定和超静定体系,计算时的收敛性更好,并且位移法每个步骤都有明确的物理意义,有助于理解和记忆。后期出现的力矩分配法和无剪力分配法都属于位移法的范畴。鉴于位移法的诸多优点[10],笔者考虑采用位移法进行分析计算。

3.2 建模

以管道支撑梁的受力情况为研究对象建立模型,图1所示某2×660 MW火电厂典型联合吊架设置形式可简化为图2所示模型。

图2 联合吊架简化模型

图2中,a点、b点、c点代表三根拉杆在管道支撑梁上的拉力作用点,Fa、Fb、Fc依次为A、B、C三根拉杆施加在管道支撑梁上的拉力,L为送粉管道之间的中心距,L1为最外侧送粉管道中心至拉杆的距离,G为单根送粉管道载荷。

3.3 解析计算

解析计算主要依据结构力学中的位移法进行。位移法以控制节点的位移为基本未知量,用位移表示控制节点处的力,根据节点处静力平衡条件,求出控制节点的位移,进而求出结构内力。位移法计算主要分为三步。第一步,通过在控制节点施加约束,将结构拆为独立的杆件基本结构。在外力的作用下,对各独立杆件进行结构分析,求出各独立杆件中控制节点处的约束力。第二步,通过对控制节点施加与原结构位移相同的位移,对各杆件进行结构分析,求出位移作用下控制节点处的力。第三步,将前两步求出的力进行叠加,并根据控制节点处的静力平衡条件,求出控制节点处的位移,进而求出结构内力。

由图2可以看出,该联合吊架模型为连续梁结构,将b点作为关键节点,b点只有角位移,没有线位移,因此这一结构属于无侧移框架体系。

根据位移法的计算步骤,在b点上施加转动约束,形成模型基本结构,如图3所示,进而将连续梁拆分成ab杆和bc杆两个独立的杆件,由此可以分别计算在送粉管道载荷G作用下独立杆件ab杆和bc杆中b点的约束弯矩MabG、MbcG。对控制节点施加角度,直至各独立杆件的变形与原结构变形一致,形成模型基本体系,如图4所示。设此时b点产生的角位移为θb,由此可以计算出角位移θb在ab杆和bc杆中b点产生的弯矩Mabθ和Mbcθ。将以上两个步骤计算得到的弯矩叠加,并考虑b点的弯矩平衡,列出平衡方程。在该方程中,仅有角位移θb一个变量,可顺利求出θb,从而求出该结构在a点、b点、c点处的反力。在计算过程中,约定弯矩方向以顺时针为正,以逆时针为负。

图3 模型基本结构

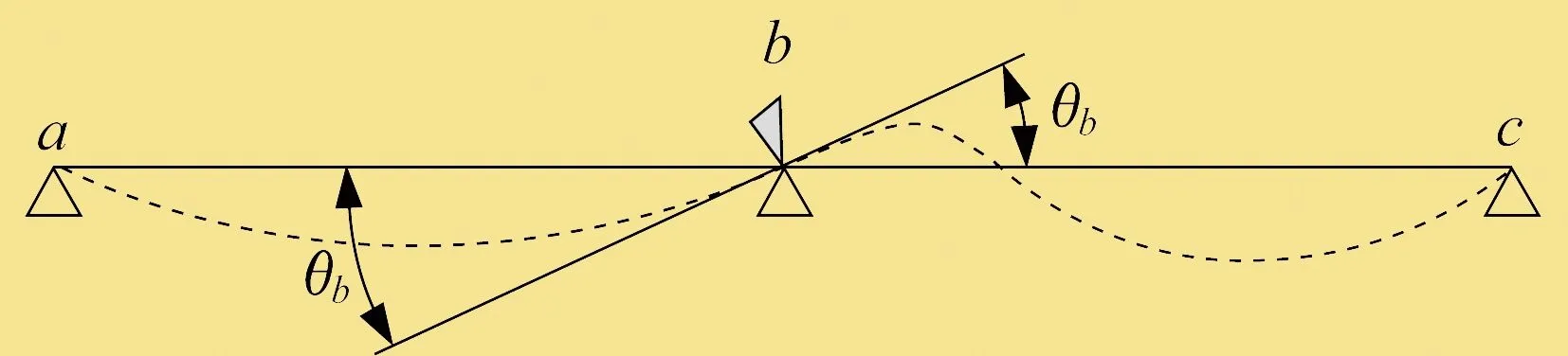
图4 模型基本体系

对独立杆件ab杆和bc杆进行计算,根据结构力学中弯矩的计算公式,可以计算出由送粉管道载荷G引起的基本结构中的弯矩:

MabG=-αGL

(1)

MbcG=αGL

(2)

(3)

b点弯矩方向如图5所示。

图5 送粉管道载荷引起的b点弯矩方向

对b点施加角位移θb,当角位移θb与原结构在送粉管道载荷G作用下的角位移相同时,约束力为0,即等效于原结构,则由角位移θb引起的b点弯矩Mabθ及Mbcθ为:

Mbaθ=Mbcθ=3iθb

(4)

i=EI/L

(5)

式中:i为独立杆件ab杆和bc杆的线刚度;E为杆件材料的弹性模量;I为杆件的惯性矩。

在实际应用中,ab杆和bc杆的规格、材质是相同的,因此两根杆件的线刚度i相等。

由角位移θb引起的b点弯矩方向如图6所示。

图6 角位移引起的b点弯矩方向

将以上两个步骤求得的弯矩分别叠加:

Mab=Mabθ+MabG=3iθb-αGL

(6)

Mbc=Mbcθ+MbcG=3iθb+αGL

(7)

在原结构中,b点受力是平衡的,由b点弯矩平衡可得Mab+Mbc=0,θb=0。因此,b点两侧弯矩Mab、Mbc为:

Mab=-αGL

(8)

Mbc=αGL

(9)

对b点左侧取弯矩,得到独立杆件ab杆的受力,如图7所示。

图7 ab杆受力

由图7可得:

同理得:

(12)

由原结构受力平衡,可得:

Fa+Fb+Fc=6G

(13)

(14)

根据上述推导计算,a点、b点、c点的支座反力计算式,即拉杆受力计算式见表1。表1中均为参数化表示,方便在不同的工程中应用。

表1 拉杆受力计算式

4 优化算法讨论

通过以上建模与推导,可以得出送粉管道联合吊架三根拉杆所承受的拉力Fa、Fb、Fc。由于L1的取值对拉杆受力存在较大影响,因此结合工程实际分三种工况进行探讨。

(1)L1=L时,边界条件为L1=L=880 mm,G=15.68 kN,且Fa=Fc=291G/343,Fb=6G-582G/343。

由传统静力矩平衡法与位移法所计算出的拉杆受力及拉杆选型见表2,拉杆型号根据《发电厂汽水管道支吊架设计手册(D-ZD2010)》选取,以拉杆直径大小表示[11]。

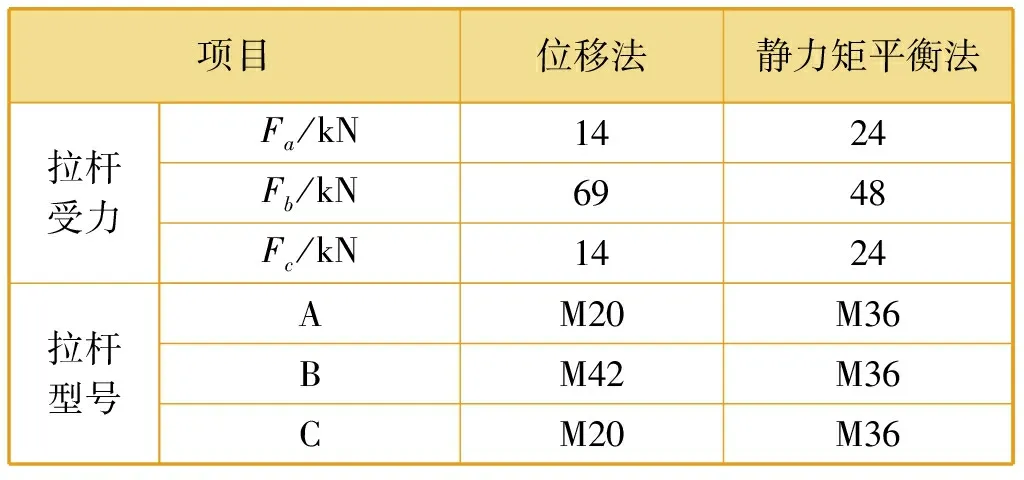
表2 L1=L时计算结果比较

由表2可知,静力矩平衡法以拉力Fa、Fb、Fc中最大者为选型载荷,导致拉杆A、C选型过大,比位移法选择的A、C拉杆型号大三档,造成材料浪费。静力矩平衡法对拉杆B所受拉力值估算偏小,拉杆选型比位移法小一档,在后期运行中可能会导致拉杆B相关组件,如拉杆、螺母、花篮螺钉、单耳吊板等变形失效和破坏,存在较大的安全隐患。

(2)L1>L时,边界条件为L=880 mm,L1=1 500 mm,G=15.68 kN。

由传统静力矩平衡法与位移法所计算出的拉杆受力及拉杆选型见表3。

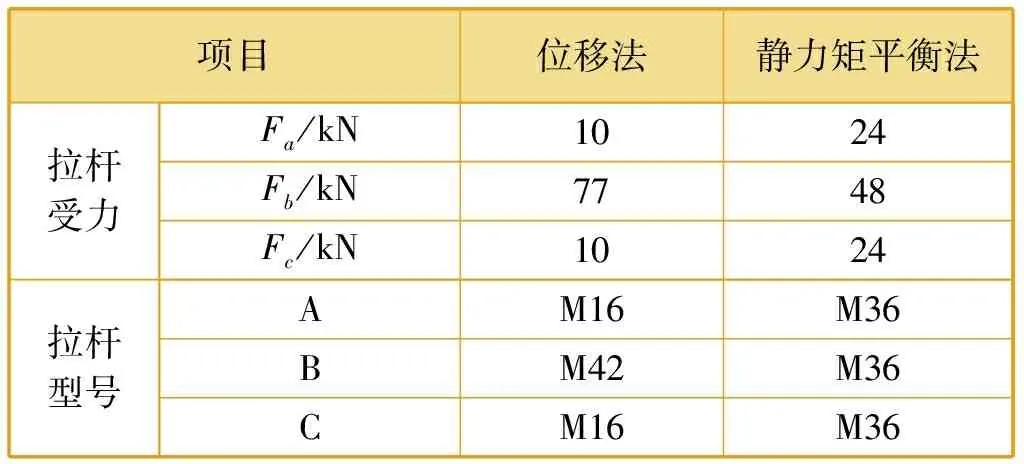
表3 L1>L时计算结果比较

由表3可知,随着L1的增大,拉杆A、C的受力Fa、Fc持续减小,再按静力矩平衡法选择拉杆型号明显不合理,采用静力矩平衡法得到的拉杆选型比位移法大四档。此外,当L1>L时,静力矩平衡法对拉杆B所受拉力值估算偏小,选型不合理,存在安全隐患。

(3)L1

由传统静力矩平衡法与位移法所计算出的拉杆受力及拉杆选型见表4。

表4 L1

由表4可知,当L1减小到一定程度后,静力矩平衡法得出的拉杆B所受拉力Fb与位移法计算结果接近,拉杆选取型号可保持一致。如果通过位移法精确计算出Fa、Fc,并据此选型,那么可以选出比静力矩平衡法小两档的拉杆型号,节省了一定的材料。

5 结束语

对于大型送粉管道联合吊架的拉杆设计,以往通过《火力发电厂烟风煤粉管道设计技术规程》中的静力矩平衡法来分配拉杆载荷,吊架选型不合理、不精确,常常会导致选型偏差较大,造成材料浪费,甚至影响运行安全。笔者通过建立联合吊架力学计算模型,推导出三拉杆超静定体系吊架的受力解析计算式,通过与静力矩平衡法对比,得出结论。当L1≥L时,应采用位移法进行吊架载荷计算,可以有效提高送粉管道运行的可靠性,降低吊架成本。当L1