切换通信拓扑条件下的无人机集群构型变换控制

刘流， 梁晓龙,2， 张佳强,3， 何吕龙， 侯岳奇

(1.空军工程大学 空管领航学院， 陕西 西安 710051； 2.陕西省电子信息系统综合集成重点实验室， 陕西 西安 710051；3.国家空管防相撞技术重点实验室， 陕西 西安 710051)

0 引言

近年来，无人机集群系统编队控制问题得到了科研及工程领域的广泛关注，并取得了大量的研究成果[1-2]。在军事领域中，由无人机或有人机组成的航空集群[1-2]可实现无源定位[3]、协同反隐身探测[4]等单个航空器难以实现的功能，类似功能的实现离不开集群所形成的特定编队构型。在集群执行任务过程中，往往需要根据不同的任务需求进行相应的构型变换。与此同时，在实际战场环境中，由于通信装备功率、带宽、距离等性能约束，如果需要保持集群间通信拓扑连通性以及对集群的有效控制，则可能需要根据情况改变集群通信拓扑关系；同时在不同作战任务中，无人机的任务角色同样可能发生变化，此时集群通信拓扑关系同样需要相应改变。因此在无人机集群通信拓扑发生变化情况下，确保对无人机集群的有效控制是研究的重点[5]。

近年来，关于集群系统的编队控制问题得到了广泛关注。文献[6]基于Leader-Follower方法，针对无人机集群系统提出了分层控制策略，以实现无人机在避障时能够保持恒定编队队形。该方法具有简单、易实现的优点，但缺点在于编队系统稳定性较差，一旦领导者出现问题，则系统难以保持稳定。文献[7]基于行为控制方式，借鉴斥力和地心偏转力的理念构造避障偏转力，该方法能够克服传统人工势场法的振荡和极小值问题，比较适用于不确定环境，但缺乏严谨的理论分析。文献[8]针对三维空间内运动的无人机集群系统设计了基于虚拟结构的编队控制器，通过一系列仿真结果证明了控制器的有效性；该方法在一定程度上可以增强编队控制的鲁棒性，但是应用范围受编队构型的影响较大，结构单一且适用性不强。

随着一致性理论的发展[9]，越来越多的学者将一致性理论用于无人机集群编队控制中。文献[10]研究了具有时延的2阶多智能体系统编队控制问题，设计了基于速度和位置一致项信息的编队控制协议，并给出了相关参数的设计方法。文献[11]研究了具有随机切换拓扑的同构多智能体系统一致性问题，并给出了实现一致的条件是通信拓扑图在任意时刻都保持连通，但是只对1阶多智能体系统进行了分析，存在一定的局限性。文献[12]研究了具有通信时延的1阶离散时间多智能体系统的一致性问题，通过引入状态预测协议对时延进行动态补偿，设计了一致性控制协议，但同样只考虑了1阶多智能体模型。文献[13]基于固定时间一致性理论研究了无人机集群的构型变换控制问题，实现了无人机集群在指定时间内达成一致并完成相应构型的变换，并利用四旋翼无人机平台进行了试验验证，但是无人机动力学模型为1阶积分器模型，只能生成相应构型，无法保持指定速度和构型。

本文结合一致性控制理论，解决了具有2阶积分特性的无人机集群在切换通信拓扑条件下的构型变换问题。通过考虑具有2阶积分特性的无人机集群模型，使得集群在进行构型变换时不仅能够完成相应构型的变换，同时能够以期望速度保持构型。通过引入编队参考向量，设计分布式控制协议，使得无人机集群能够实现特定构型的变换，同时保持期望速度与相应构型，便于后续作战任务的执行，最后通过数值仿真验证了理论的有效性。

1 图论预备知识

考虑一个多智能体系统，将每个智能体视作节点，则智能体网络拓扑常用有向图G=(W,E,A)来描述，其中W=(w1,w2,…,wn)为非空有限的节点集合，E={(wi,wj):wi,wj∈W(G)}为边集，A=[aij]∈RN×N为非负邻接矩阵，其中n、i、j为下表索引自然数，N为矩阵空间维度自然数。图G中：若节点i与节点j之间存在信息交换，则存在边(wi,wj)；若信息交换是没有方向性的，即(wi,wj)∈E⟺(wj,wi)∈E，则称图G为无向图；若信息流只从节点j流向节点i，即边是有方向性的，则称图G为有向图,可以将无向图看作有向图的特殊情况。如果在任意两个节点之间都存在至少一条路径，则图G为连通的。记节点i的邻居节点为集合Ni⊆W(G)，即Ni={wj∈W:(wi,wj)∈E}。若wj∈Ni(i≠j)，则aij>0，否则aij=0.G图的Laplacian矩阵L=[lij]∈RN×N定义为

(1)

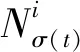
2 集群构型控制问题描述及控制协议

考虑由N架无人机组成的无人机集群，无人机间的通信拓扑由无向图G表示，其中每架无人机为图G中的节点wi，i∈{1,2,…,N}. 将每架无人机视作质点，其动力学模型为2阶动力学模型[14]：

(2)

式中：xi(t)、vi(t)、ui(t)分别为无人机wi的位置、速度、加速度，xi(t)∈R1，vi(t)∈R1，ui(t)∈R1,同时ui(t)也为无人机wi的控制输入，1表示元素全为1的相应维数列向量。为了便于描述，本文在一维情况下进行分析，但所得结论仍然适用于二维平面及三维空间。

定义ξi(t)=[xi(t),vi(t)]T，B1=[1,0]T，B2=[0,1]T. 则无人机集群系统(2)式可以表示为

(3)

定义1∀i,j=1,2,…,N，如果存在Ri(t)=[Rxi(t),Rvi]T∈R2，使得

(4)

则称无人机集群实现了期望构型及期望速度，其中r为参考向量。

为使无人机wi在切换通信拓扑条件下实现期望构型变换，设计如下控制协议：

(5)

式中：K∈R1×2为常数参数矩阵；α为常数参数。

在控制协议(5)式中，第1项为使无人机达到期望速度，第2项为控制一致项。无人机wi的邻居个体会随着通信拓扑的切换发生变化。需要指出的是，在控制协议(5)式中并未考虑无人机间的避撞问题。为了确保无人机集群运动的一致性，并对相关定理进行理论推导证明，未在控制协议中加入势函数等避撞项，以免无人机集群在构型变换过程中出现振荡等现象，在实际飞行中可采取为无人机划分不同高度层的方法来避免无人机相撞。

在控制协议(5)式下，将系统方程(3)式表示为矩阵形式：

(6)

3 控制协议设计问题转化

对无人机集群系统(6)式进行转化，将其转化为两个子系统，一个主要用来描述编队误差系统，另一个用来形成期望编队构型。通过证明可以看出，无人机集群形成期望构型等价于误差系统实现渐进稳定。则控制协议(5)式的设计转化为设计合适的参数，使得误差系统实现渐进稳定。

(7)

为便于后文进一步的研究，还需要以下引理。

引理1对于任意σ(t)∈Q，如果Gσ(t)是连通的，则Lσ(t)只有一个零特征值[15]，其余特征值均为正。

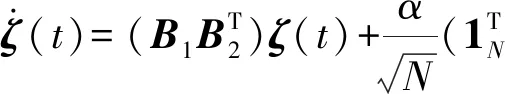
(8)

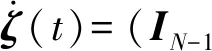
(9)

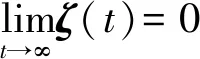
证明取e1∈RN，为首行元素为1、其余元素为0的N维列向量。定义

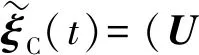
(10)

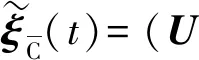
(11)

因为[ζT(t),0]T=e1⊗ζ(t)，则(10)式可以表示为

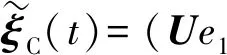
(12)

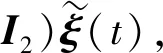
(13)

由(12)式、(13)式可得

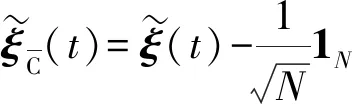
(14)

4 主要结果证明

下面给出无人机集群系统(6)式在通信拓扑切换条件下实现期望构型变换的充要条件，同时给出控制协议中参数矩阵K的设计方法。

定理1具有切换通信拓扑的无人机集群系统(6)式，实现期望构型变换的充要条件为当且仅当：

1)对于所有的i∈{1,2,…,N}，

(15)

2)下述切换通信拓扑线性系统趋于渐进稳定，

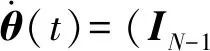
(16)

式中：θ(t)为系统(16)式的状态变量。

证明必要性。如果无人机集群系统(6)式能够实现期望构型变换，则根据引理2和(9)式可知:

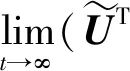
(17)

且下述系统

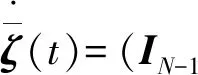
(18)

=-1N-1.

(19)

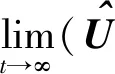
(20)

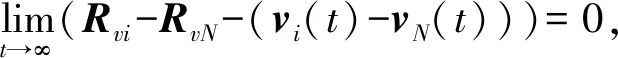
(21)

条件1得证。

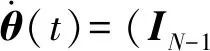
条件2得证。

充分性。如果满足条件1，可得

(22)

则

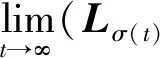
(23)

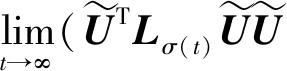
(24)

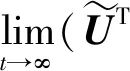
(25)

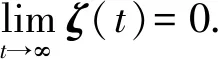
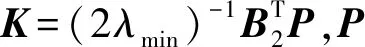
(26)

证明考虑系统(16)式的稳定性，构造如下Lyapunov函数：

V(t)=θT(t)(IN-1⊗P)θ(t),

(27)

将V(t)对时间t求导，可得

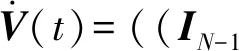
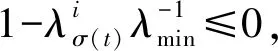
5 仿真结果与分析

考虑由4架无人机组成的集群系统，在二维平面运动并进行构型变换，仿真中涉及到的位置单位为m，速度单位为m/s，加速度单位为m/s2. 假定存在由4个不同通信拓扑关系组成的集合S，如图1所示。无人机集群系统的通信拓扑每隔10 s在集合S中进行随机切换，拓扑切换信号图如图2所示。

无人机集群系统相关系统矩阵为

(28)

式中：i=1,2,3,4；xix、xiy分别为无人机wi的北向位置和东向位置；Rxvi、Ryvi分别为期望速度向量的北向和东向分量；vix、viy分别为无人机wi的北向速度和东向速度。

无人机集群系统初始位置为

初始速度均为0.

编队期望速度为Rxvi=2，Ryvi=0.5. 期望构型矩阵为

(29)

式中：Rxx(t)为期望构型北向位置分量；Ryx(t)为期望构型东向位置分量。

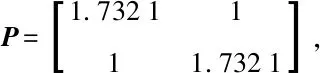
(30)

仿真步骤流程图如图3所示。

由于本文在控制协议设计过程中并未考虑机间避撞问题，在实际飞行过程中，可通过为无人机设置不同高度层来避免相撞问题。图4所示为无人机运动轨迹图。

6 结论

本文研究了在通信拓扑切换条件下的无人机集群系统的构型变换控制问题。针对连续2阶积分器模型，通过引入编队参考向量设计了一致性构型变换控制协议，并给出了参数矩阵设计方法以及实现并保持期望构型的充要条件。通过仿真验证了所设计控制协议的有效性。