软固结磨粒群微观力学特性分析与试验研究

计时鸣， 邱文彬， 曾晰， 郗枫飞， 邱磊， 郑倩倩， 石梦

(浙江工业大学 机械工程学院 特种装备制造与先进加工技术教育部重点实验室， 浙江 杭州 310014)

0 引言

软固结磨粒气压砂轮作为一种新型柔性抛光方法[1]，其密集磨粒群被约束在工件与柔性支撑介质之间的狭小区域内，宏观上随支撑介质保持运动规律一致，微观上内部相互作用形成挤压，使表层磨粒群在二者耦合作用下实现工件表面材料的去除。软固结磨粒气压砂轮由橡胶基体构成空心半球，表面通过高分子黏结剂固结一层有一定体积分数的磨粒，标记橡胶基体为内弹性层、磨粒黏结层为外弹性层，通过向内弹性层中充入压缩气体控制压力，其基本结构如图1所示。这种柔性抛光方法的磨粒群整体在支撑介质表面相对位置固定，易通过介质实现自动控制，从而可提升加工方法自动化程度，同时加工过程中的磨粒群具备局部自由空间，这一特性使该方法适用于多种加工对象。

软固结磨气压砂轮在具备独特加工优势的同时，磨粒群在表面随机微动产生的微划痕、微裂纹成为影响表面光洁度和加工效率的主要因素。王卓[2]和蔡立等[3]用电子显微镜观测发现，在面向光学元件的柔性抛光首次加工中，每平方厘米抛光表面有3万条深8～70 nm的微痕，约占抛光总面积的10%～20%. 要保证光洁度只能采取进一步精抛加工，若在大型模具和光学元件加工中，则加工耗时将进一步提升。目前针对提升柔性抛光方法加工效率的研究主要集中在以下几种：1)通过柔性支撑介质进行运动控制，使加工轨迹呈现方向性，进而控制加工质量[4-5]；2)通过对施加载荷进行控制，在保证面型精度的同时，提升表面加工精度[6-7]；3)通过改变加工工具整体特性来适应加工环境[8-10]。上述方法只考虑了宏观参数的影响，而忽略了磨粒群微观相互作用，将对柔性抛光方法的深入研究造成瓶颈。

在颗粒物质力学中，软固结磨粒群被当做离散颗粒物质的集合体，磨粒间相互离散接触，剪胀性是其基本特性之一[11]。磨粒群的应力通过颗粒的接触进行传递，而应变则由颗粒间的相对滑动产生，即颗粒材料力学特性主要取决于颗粒间的接触。颗粒间的材料力学特性可以用微观力学理论来描述[12-15]。

本文针对软固结磨粒群内部微观力学特性，对被加工材料表面划痕的影响规律展开研究。首先针对气压砂轮柔性特征，结合颗粒物质接触模型和剪胀效应，建立磨粒之间的力学接触和力- 位移本构模型；其次采用离散单元法的颗粒流理论，模拟软固结磨粒群力学接触模型和加工件的表面受力情况，分析在不同微观参数下表层磨粒群力链传递及加工件的受力变化关系；最后通过材料光整加工试验，验证软固结磨粒群的内部磨粒微观力学特性对被加工材料表面划痕的影响。

1 磨粒群微观系统的特性分析

1.1 软固结磨粒群的微观力学模型

磨粒在软固结形态下通常呈现为密集的颗粒系统，且颗粒间存在相互约束，粒子间接触力成为决定系统变形或流动的主要因素。JKR接触理论[16]基于Hertz接触理论，考虑了颗粒接触表面的黏结作用，将接触面积与弹性材料特性和表面作用强度联系起来，使用该模型作为软固结磨粒的法向接触模型。

图2所示为两个颗粒的法向接触模型。图2中：a为考虑粘连力的两颗粒接触面半径；虚线为不考虑变形时颗粒表面所在的位置；N为外载荷。

根据图2，两个颗粒在外载荷N和表面粘连力共同作用下的等效载荷力N1[16]可表示为

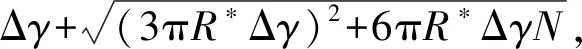
(1)

(2)

Δγ=γ1+γ2-γ12，

(3)

式中：R*为有效颗粒半径；Δγ为Dupre粘连能；R1和R2为接触颗粒的半径；γ1、γ2和γ12分别为两颗粒表面的自由能和界面能。

对于切向接触力，由于在密集颗粒系统内，粒子间发生了持续接触且存在运动趋势，但相互间并没有产生相对滑动，切向力也明显小于滑动摩擦力。Thornton[17]于1991建立了粘连颗粒间的理论，考虑了颗粒塑性变形和加载历史等因素的影响，应用(4)式可建立磨粒间的切向力接触模型：

T=8G*aδ，

(4)

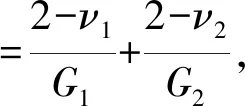
(5)

式中：T为磨粒间的切向力；G*为有效剪切模量；δ为剪切位移；G1和G2为两颗粒的剪切模量；ν1、ν2为两颗粒的泊松比。

基于上述理论，通过分析颗粒间法向和切向接触力，为磨粒群微观形变规律研究建立了理论基础。

1.2 软固结磨粒群剪胀本构模型

软固结磨粒群是由高聚物黏结剂黏结于橡胶基体表面的磨粒群体，微观上每个磨粒均受到黏结剂在各个方向的弹性支撑，每颗磨粒受力后不但可局部微动、不脱落但有位移和姿态变化，而且可能影响周边磨粒的受力状况、发生群体效应。上述现象对加工的影响主要包括切削力传递不稳定引起的材料去除率减小，以及切削表面不稳定造成的加工表面质量不均匀。软固结磨粒群的这种力学特性表明，借助颗粒物质的剪胀理论可对磨粒群内部的微观变形开展进一步研究。

颗粒物质的剪胀研究表明[18]，在加载时，孔隙率大的磨粒群内部主要发生体积剪缩效应，孔隙率小的颗粒群内部主要发生体积膨胀效应。图3所示为颗粒群内部剪胀效应简图，其中σ为法向力，τ为切向应力。

磨粒群的剪胀性可用剪胀方程(描述应变分量之间比例关系的公式)来描述。将塑性体应变增量与塑性剪应变增量之比定义为剪胀比[19]：

(6)

磨粒群内部在形变过程中会出现相变状态，即磨粒群在体积变形由压缩到开始膨胀的突变状态[20]。将当前孔隙率和相变孔隙率的比值作为相变状态参量，引入剪胀方程，建立与内部状态和应力水平相关的剪胀方程表达式为

(7)

(8)

(9)

(10)

式中：d0和m为模型常数；ψ为状态参量；η和M分别为当前应力比和相变应力比；e(p′)和ept(p′)分别为当前孔隙率和相变孔隙率；p′=(σ1+σ2+σ3)/3为有效平均应力，σ1、σ2及σ3分别为第1主应力、第2主应力和第3主应力；σ1pt、σ3pt分别为相变状态的第1主应力和第3主应力。

为反映磨粒群在旋转加工过程中的变形特性，需要建立磨粒群的剪胀本构模型。基于状态相关剪胀理论，对应于(7)式，磨粒群剪胀本构模型如(11)式所示：

(11)

式中：q为广义剪应力；p′为有效平均应力；

(12)

G0为材料参数，pa为标准大气压；

(13)

G和K分别为磨粒的剪切模量和体积模量，υ为泊松比；Kp为塑性模量，隐含了材料的硬化概念，

(14)

h和n为两个模型参数；dεq为剪应变增量；dεv为体应变增量。(11)式为Li等[21]建立的弹塑性本构模型，该模型反映了颗粒物质的各种变形特性，借鉴该模型可以研究磨粒群的微观形变。

2 软固结磨粒群的数值模拟

由于软固结磨粒气压砂轮是旋转加工，导致软固结磨粒内部不断处于变化状态，外部的磨粒也随之变化。内部磨粒的滑动、旋转重组必然影响内部力的传递和稳定。软固结磨粒群内部颗粒之间通过黏结剂粘连在一起，同时黏结剂也对颗粒产生了一定的弹性支撑。因此在颗粒流三维分析PFC3D软件中选择平行黏结模型，作为磨粒群接触的本构模型来描述磨粒群内部颗粒受力和弯矩，更符合磨粒群的实际特征。平行黏结模型特征参数如表1所示。以下的接触力仿真和磨粒群微观变形都是基于该接触模型。

表1 平行黏结模型特征参数

2.1 磨粒群接触力传递

通过PFC3D软件建立软固结磨粒群模型如图4所示，基础参数设计如表2所示，对磨粒层施加F=1 MPa的压力，通过改变磨粒群孔隙率，得到4组不同磨粒层内部结构变化的量化参数如表3所示。

基体半径/mm磨粒层厚度/mm磨粒数摩擦系数405100000.18

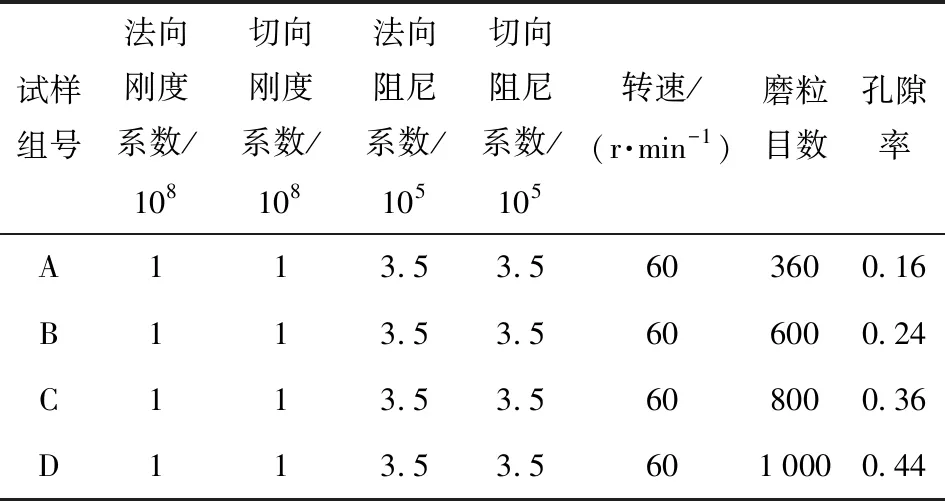
表3 不同孔隙率磨粒群参数表

在软球接触模型下，为了避免磨粒磨损产生的计算误差，设定颗粒接触时的重叠厚度δmax≤30%R(R为基体半径)。依照表3中的参数进行接触力网的仿真，并对单颗磨粒在软固结形态下的法向接触力和切向接触力进行了验证。

如图5所示为不同孔隙率下磨粒群的接触力网中心截面图，其中黄色颗粒表示磨粒，红色线条表示力网。

通过改变磨粒群的孔隙率，即改变磨粒群的体积分数、磨粒接触面积等，可以形成不同的接触力网以适应加工需求。这里的接触力网是指颗粒之间接触使得颗粒间相互挤压变形而形成的力传递路径，每个颗粒与其他颗粒相接触的个数即配位数不定，造成其方向的各向异性。由图5可知，在应力传递过程中，孔隙率小的磨粒群接触力网表现为密集，强力链占大多数，最终传递到工件表面的力链较多；随着孔隙率的增大，磨粒的配位数减小，内部颗粒平均接触数目减小，接触力网变得稀疏，力链传递衰减，当孔隙率超过44%后，力链传递几乎消失。图5的仿真结果表明可通过控制磨粒群的孔隙率改变切削力。

在上述条件下，从磨粒群样本中选取单颗磨粒进行应力仿真。并依照(1)式和(4)式进行计算，对合力取平均值，所得结果如表4所示。

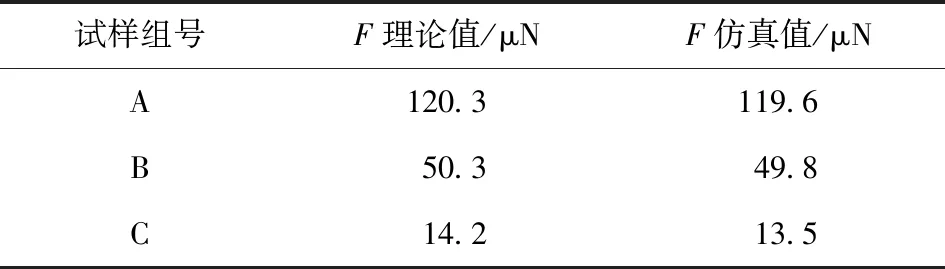
表4 单颗磨粒应力分析结果

通过上述对比可以发现，仿真结果往往低于理论计算，这是因为磨粒群蠕动导致相对速度微变造成的，但最终计算误差可以控制在1%以内，理论计算模型基本可以使用。

2.2 磨粒群内部微观变形

根据表3的仿真参数，设置下压量l=1 mm，可得到4组不同孔隙率下表层磨粒对加工件表面的应力变化图如图6所示。

从图6中可知如下软固结磨粒气压砂轮加工规律：1)在软固结磨粒旋转加工下，工件表面受力产生了周期波动，波动时间间隔在0.3 s左右。这是因为软固结磨粒气压砂轮作为一种柔性加工方法，在旋转加工过程中，表层磨粒群与工件的接触数目并不是固定的，其受到剪胀效应的影响。这种影响主要体现在磨粒接触数的动态性，其波动周期主要受砂轮的转速和磨粒群的剪胀性的影响。2)当孔隙率在0.16～0.24范围内变化时，工件受力处于较均匀状态，最终稳定在0.68～1.20 MPa之间，随着孔隙率的增大，表面受力整体螺旋增加。上述现象的发生是通过软固结磨粒群自身的特点表现出来的：软固结磨粒群是磨粒和黏结剂的混合体，属于一种密实的颗粒物质，一方面，在加载初期和旋转加工过程中受孔隙均匀化影响[22]，大孔隙优先减小、引起磨粒群发生剪缩；另一方面，软固结磨粒群受到黏结剂的弹性支撑，而且加工的下压量几乎保持不变，在磨粒群不发生结构性破坏的前提下，内部结构会重新排列，导致磨粒群在相变状态中总体保持动态平衡。因此，为保证加工均匀性，应采用可以使工件受力较均匀的小孔隙率磨粒群抛光工件，从而改善抛光工件表面划痕。

3 试验及讨论

3.1 软固结磨粒群的制备及试验系统

考虑气压砂轮表面软固结磨粒群在加工过程中会发生自锐现象，在制备气压砂轮时，需要选择适当的磨粒和黏结剂。棕刚玉具有硬度中等、韧性大、颗粒锋锐、价格较低廉、适合加工抗张强度高的金属等特点，为此选择棕刚玉作为试验磨粒。由于黏结剂的选择直接关系到磨粒的固结效果，通过对比树脂类黏结剂、热固黏结剂、耐高低温黏结剂等数十种黏结剂在橡胶基体黏结、磨粒附着、自身耐磨性等方面的效果，发现酸性硅酸酮密封胶具有良好的磨粒黏附效果，并与橡胶基体具有良好的黏结效果，可供磨粒固结使用[23]。

采用日本安川公司生产的Montoman-HP20型工业机器人构建软固结磨粒气压砂轮光整加工试验系统，实现加工过程的位姿和轨迹控制。软固结磨粒气压砂轮制备系统以及光整加工试验系统如图7和图8所示。

根据表2和表3配置相应的磨粒和黏结剂，均匀混合后，将橡胶基体套在上模中，然后将一定量磨粒黏结剂手动注入下模具，上模下压，由电动机带动上模旋转至表面均匀，手动取下气压砂轮，进行自然固化，最终制备成3组软固结磨粒气压砂轮(参数见表5)，每组18个。

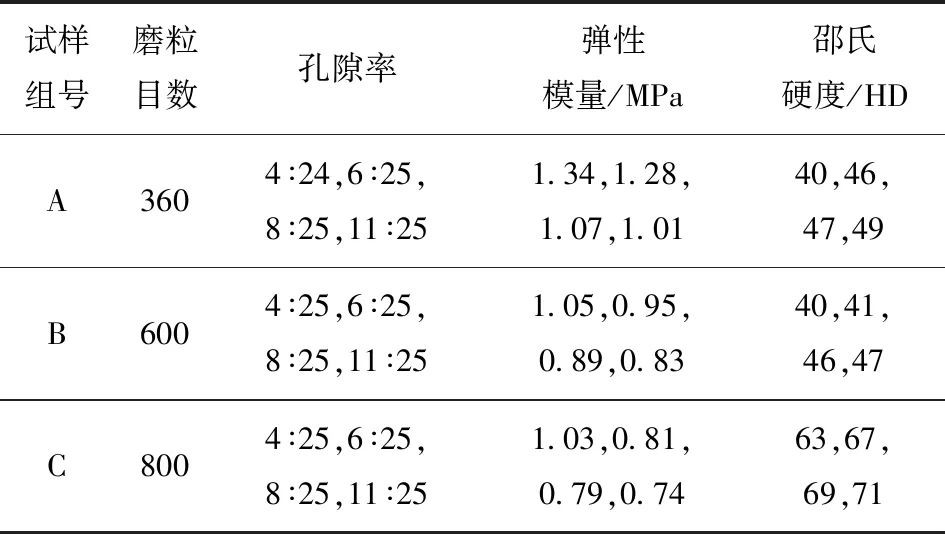
表5 软固结磨粒层参数表

3.2 软固结磨粒群的光整试验和结果分析

以表6所示的参数作为试验条件，分别采用表5所示3组软固结磨粒群，对硬度为434HV、表面粗糙度为313.74 nm的模具钢P20试样进行加工(见图9)，其初始微观形貌图如图10所示。设置加工路径为a到b，每次循环加工次数设置为40次。

表6 加工参数设计

3组试样经过往复加工40次后，利用美国维易科公司生产的Wyko NT9800 Veeco白光干涉仪检测工件表面的粗糙度，发现各组粗糙度存在差异(见图11)。由图11可知：随着磨粒群孔隙率的增大，工件表面粗糙度值在下降，孔隙率为0.16的工件表面粗糙度值下降较快，当孔隙率超过0.44后，表面粗糙度值几乎不再下降。根据2.1节的仿真结果，随着孔隙率的增大，力链传递减弱，有效切削力减小；同时还发现随着磨粒目数的增大即磨粒粒径的变小，工件表面粗糙度下降，当孔隙率为0.24、磨粒目数为800时，工件表面粗糙度减小效果最明显。磨粒目数为800、孔隙率为0.24的磨粒群加工工件微观形貌图如图12所示。

从图10初始微观形貌中可以看出，加工前工件表面划痕较多，划痕深度十分不均匀，在长245.30 nm的取样范围内，轮廓算术平均偏差Ra为313.74 nm，微观不平度十点平均高度为2.35 um. 从图12中可以发现，采用优化后的工艺参数即磨粒目数为800、孔隙率为0.24的软固结磨粒群加工，工件表面粗糙度Ra降低到67.11 nm，轮廓最大高度Rz降低到737.34 nm，划痕得到有效的减少。

4 结论

本文建立了磨粒群内部微观接触力模型，分析了磨粒群内部力链传递问题。引入Li-Dafaias弹塑性剪胀本构模型，分析了磨粒群内部微观力- 位移的联系。所得主要结论如下：

1) 在磨粒群内部应力传递过程中，孔隙率小的磨粒群接触力网表现密集，强力链占大多数，最终传递到工件表面的力链较多。随着孔隙率的增大，磨粒的配位数减小，内部颗粒平均接触数目减小，接触力网变得稀疏，力链传递衰减，当孔隙率超过44%后，力链传递消失。

2) 使用磨粒群加工工件时，工件表面受力产生0.3 s的周期波动，当孔隙率在0.16～0.24范围内变化时，工件受力处于较均匀状态，最终稳定在0.68～1.20 MPa之间。

3) 磨粒群孔隙率和材料表面粗糙度存在对应关系，磨粒目数对材料粗糙度存在影响。在本文试验条件下，采用目数为800和孔隙率为0.24时的磨粒群加工得到的工件表面粗糙度较小，表面粗糙度Ra从313.74 nm降低到67.11 nm.