基于谐波集检测的飞行目标水下声探测算法研究

穆森， 李京华， 张恒， 陈果

(1.西北工业大学 电子信息学院， 陕西 西安 710072; 2.陆军研究院 近地面探测技术实验室， 江苏 无锡 214035;3.宜昌测试技术研究所， 湖北 宜昌 443003)

0 引言

反潜直升机对于水下潜艇具有很大的威胁，为了提高水下潜艇对抗反潜机的能力，有必要尽快解决水下对空探测的技术问题。反潜直升机飞行时，旋翼辐射噪声的声波穿越空- 海界面入水后形成的频谱具有谐波特性，为水下探测空中反潜飞机提供了可行途径。

目前关于被动声探测的研究多集中在同一种介质内，如空气介质中的声探测或海水介质中的水下声探测。魏丽萍等[1]给出了谐波集(HS)检测算法，并成功地对实测的空气中直升机声信号进行了HS检测；马宁等[2]提出了一种基于小波包和神经网络的检测算法，可以较好地检测识别不同型号的空气中直升机信号；Salloum等[3]开发并建立了一个声学空气检测(AAD)系统，实现了空中目标的检测和跟踪，并对小型飞机、直升机和超轻飞机进行了分类；周关林等[4]提出随机共振水声信号的检测，为检测水下微弱信号提出了新思路。关于空中飞行目标的水下声探测，即空气- 水跨界声探测问题的研究大多集中在空中声源激发的水下声场理论建模方面，而空中目标的水下跨界检测算法则研究很少。例如：以色列研制了潜艇反直升机和低空慢速飞行目标的声探测浮标[5]，用于检测海面上空目标的声信号；韩建辉等提出在水下检测空中声源的平滑伪维格纳·维尔分布- 高度门限(SPWVD-HT)算法[6]、双谱幂次法[7]，但所检测声信号均采用空中运动声源激发的水下声场建模仿真信号。

本文提出基于HS检测与最强谱线检测相结合的检测算法，根据背景噪声进行自适应门限计算，并对功率谱中HS进行检测，若HS不存在，则将最大线谱谱峰与门限进行比较，判断目标是否出现，以实现空中移动声源的水下跨界检测。应用该算法对水下单水听器接收的螺旋桨飞机飞行噪声实测信号进行了目标检测仿真，并对该算法的检测性能进行了分析。

1 飞行目标噪声及入水传播特性分析

带有螺旋桨的飞机在飞行时会有较大的噪声，尤其是直升机飞行时，其辐射噪声主要由主桨、尾桨和发动机产生。噪声可分为气动噪声和机械噪声两大类[8-9]，机械噪声属于高频噪声，传播到空气中很快被吸收，其噪声源只对飞机近场噪声起作用；气动噪声主要集中在频谱的低频部分，对远场噪声起决定性作用，功率较强且持续不断。由于直升机旋翼在结构上有周期转动机制，其远场噪声功率谱是由具有谐波关系的离散线谱叠加于宽带连续谱上构成的，呈谐波关系的频率分量构成一个HS。例如，直升机由于有主桨和尾桨，通常由两个不同基频的HS组成，某直升机的时域波形和功率谱如图1所示。图1(b)中的慢变曲线是分离出的趋势项波形，其中*和∘表示频谱中离散线谱构成的两个HS，分别对应主桨桨叶通过频率(BPF)及其各次谐波频率，以及尾桨BPF及其各次谐波频率。

螺旋桨BPF用fBPF表示，它对于某一种螺旋桨飞机而言是一个固定常数，可由(1)式计算[10]：

fBPF=iwr/60，

(1)

式中：i为谐波次数；w为桨叶个数；r为转速。当飞机改变速度和状态时，螺旋桨旋转速度不变，fBPF的值也不变。

一般检测问题中假设噪声为平稳高斯随机过程，然而对于水下探测，由于目标和传感器周围的环境条件(尤其是风速和海浪)影响，有可能改变噪声的统计特性，成为非平稳非高斯过程。为便于处理，基于微分法思想，假设噪声在一个非常短的时间内保持平稳，可将其视为平稳信号，故信号处理时将数据分为若干个短数据段进行。

空气中点声源发出的声波传播入水过程会有较大衰减。按照波动理论[11]，在满足空气中点声源高度要求和声传播路径的相位变化条件基础上，空气中高度为h的点声源可以等效为水中深度为d的点声源，同时其声压级衰减20lg(kαd)，其中kα为声波在空气中的波数。图2所示为空气中点声源的水下等效源[11]示意图，直观地表明了空气中点声源可等效为水下声源加上空气声源到水面的传播衰减。

因此可将声源空气- 水跨界传播问题转换为水下声传播问题，进而分析水下声场。根据对波动方程解法的不同，本文选取基于抛物方程的RAMGEO模型进行仿真计算，该模型改进了抛物方程模型，并与稳定的自身初始场结合[12]，适用于浅海低频噪声环境。本文具体仿真参数如下：声源深度10 m，声源频率200 Hz，接收水听器在水下呈垂直线阵排布，海水深度250 m. 利用RAMGEO模型仿真计算得到的声源水下传播衰减趋势如图3所示。

由图3(a)可以看出，声源在水下环境水平距离200 m以内的范围大致呈线性衰减，水平距离每增加约10 m，声压级降低2 dB，在水平距离超出200 m范围后，声压级衰减明显减小。这表明只要声源声压级足够大，声波就可以实现在海水介质中的远距离传播。声源在深度范围上的衰减如图3(b)所示。由图3(b)可以看出，在浅海环境下水深100 m之后，声波传播衰减趋势发生了较大变化，这可能是因为海底声波反射以及底层泥沙沉积物引起的声能损耗造成的。

由于海上直升机目标往往带有较大的噪声声压级，按照等效源理论完全可以满足声波的远距离传播，从而为海上战场声目标的探测提供了有力手段。

2 基于自适应门限的HS检测算法

2.1 算法原理

目标检测基于以下两种假设：1)H0-没有目标；2)H1-目标出现。检测算法原理框图如图4所示。

由图4可知，本文提出的检测算法是一种在频域中采用HS和最强谱线检测相结合的检测方法，首先需要计算采集信号功率谱和背景噪声功率谱拟合曲线，并根据拟合曲线计算检测门限(DT)，在功率谱中搜寻线谱，将线谱按谱峰高低进行降序存储，若在搜寻的若干个线谱中有2个以上存在谐波关系，则认为有HS并判断为目标出现，输出状态为H1；若没有HS，则将谱线中最强的谱线峰值与DT进行比较，该门限由背景噪声功率谱拟合曲线确定：若大于DT，则判断为目标出现、状态为H1，否则判断为没有目标、状态为H0.

2.2 HS检测

HS检测时，必须首先对水听器接收信号时间序列采用Welch法[13-14]计算功率谱：

(2)

式中：PSD(f)为接收信号的功率谱；M为数据窗长度；L为数据段总数；xb(n)为第b个数据段中的第n个数据，b=1,2,3，…；d(n)为第n个数据的窗值。

在HS检测过程中，线谱的判断是算法中至关重要的一步，如第1节所述，螺旋桨飞机声信号的特征频率(基频)及其谐波集中在中低频段，因此线谱检测过程中首先需要选择相应的频率范围，然后进行线谱搜索和判定。在选定频段内以滑动窗搜索所有谱峰，按谱峰值大小降序排列，选用前几个线谱谱峰做HS检测。线谱的搜索及判定方法如下：

1) 线谱值必须是功率谱中的局部极大值Lmax，该极大值对应的频点为fk(k=1,2,…,K，K为线谱数量)，局部极大值判断过程是：将当前检测点k的功率谱值分别与其左、右相邻点k-1和k+1的功率谱值求1阶差分Δl和Δr，若满足Δl<0且Δr>0，则Lmax暂定为此邻域内的局部极大值；

2) 若步骤1中Lmax的大小在k点的左、右峰宽Lsize邻域范围内均为最大值，则Lmax暂定为线谱峰值；

3) 类似于步骤2，若在Lmax点的左、右峰宽Lsize邻域范围内，分别存在极小值Lminl和Lminr，且比值2×Lmax/(Lminl+Lminr)大于某个阈值，则可认为谱峰Lmax是显著的，可将fk频点处的Lmax作为线谱；

4)Lmax谱线的峰高定义为

hs=|Lmax-(Lminl+Lminr)/2|，

(3)

从而线谱的选取兼顾了谱峰左右边界、峰宽和峰高等特征判据，对线谱特征的辨识度较高。

HS检测按照以下方程[15]判断：

|fk/fm-imk|≤ε，

(4)

式中：fm为假定基频，m为主桨和尾桨基频个数，m∈(1,2)；imk为谐波次数，imk=1,2,3；ε为选定的阈值。

若检测到若干线谱对应的频率与该假定基频有明显的谐波关系，则认为检测到一个HS，该假定基频即为HS的基频。HS构建策略如下：

1) 根据线谱搜索及判定方法进行线谱检测；

2) 根据线谱峰高hs的大小，选出若干峰高较大线谱的频点fk；

3) 将K个线谱的频点依次作为假定基频fm，例如将第m个频点作为基频，其他K-1个频点fk用(4)式进行谐频检测，即只要(4)式中imk取值为2或3时fk满足(4)式，即可认为fk与fm具有谐频关系，它们对应的线谱具有谐波关系。

在检测中对于某个基频，有时会出现不止一个HS，这时需要用权函数决定取舍，对每个HS内所有频率的能量进行计算并作为权值，选择具有最大能量的HS，与其对应的基频作为提取的螺旋桨飞机特征频率。

在HS检测中，由于谐波信号特性不同，例如频率检测范围、线谱个数、线谱谱峰宽度、HS内谐波数目以及阈值等参数，需要对实际信号进行分析后确定这些参数的最佳值，从而使谐波检测效果最佳。

2.3 自适应DT的计算

由2.1节的算法原理可知，在进行目标检测时首先进行HS检测，若没有HS则寻找线谱中最强的谱峰，并与DT比较，若目标出现，则由目标发出的噪声级再加上背景噪声的噪声级就会大于该DT. DT计算公式为

TDT=α+P(f)，

(5)

式中：TDT为实际计算检测门限DT；α为门限调节因子；P(f)为无目标时背景噪声信号功率谱的多项式拟合曲线。在实际环境中，背景噪声的大小是变化的，为了使检测门限能自适应地随之调整，本文提出采用α来动态调节门限，它可以根据无目标时不同环境下测得的P(f)来计算，使DT成为随环境变化的自适应门限。

一般情况下，实际背景噪声发生变化的主要原因是环境变化使得某一部分频率分量的噪声能量增加或减少，从而造成背景噪声功率谱曲线[16]上某些频率分量的功率谱幅度增大或减小，因此这种变化是一种非线性变化，在缺乏先验知识的条件下，对这种变化进行定量描述是很困难的。因此本文提出采用最小二乘法对背景噪声功率谱进行拟合，从而对背景噪声级进行近似定量描述，α和DT的计算过程如下：

1) 计算第l帧背景噪声nl(t)的功率谱，并取分贝数后为

Pn(f,l)=10lg(PSDn(f,l))，

(6)

式中：Pn(f,l)为第l帧背景噪声的功率谱分贝数；PSDn(f,l)为第l帧背景噪声的功率谱幅值。

2) 对Pn(f,l)采用最小二乘法进行曲线拟合，设拟合多项式的阶数为k，第l帧的拟合公式为

P(f,l)=p1fk+p2fk-1+…+pkf+pk+1，

(7)

式中：P(f,l)为第l帧背景噪声的功率谱拟合曲线；pk为拟合系数，拟合曲线如图5中背景噪声中的连续实线。

3) 门限调节因子α的计算示意如图5所示，图5中背景噪声功率谱最大值对应的频点为fα，则α取值为背景噪声功率谱的最大值(图5中黑色实心圆点)与其拟合曲线P(f,l)在fα频点取值的差值，第l帧门限调节因子α的计算公式为

α(l)=max[Pn(f,l)]-P(fα,l) ，

(8)

式中：max[Pn(f,l)]为第l帧背景噪声功率谱的最大值；fα为第l帧背景噪声功率谱最大值对应的频率值；P(fα,l)为第l帧背景噪声功率谱频率值为fα时对应的拟合曲线值。

4) 根据第l帧背景噪声计算的判决门限DT为

TDT(f,l)=α(l)+P(f,l).

(9)

从(9)式可知，这样计算出的门限值是一个随频率变化的动态曲线，且随着时间的变化而变化。

3 实测信号检测实验及结果分析

3.1 实测信号检测实验

采用实测数据对本文算法进行验证。实测数据的时域波形和时频谱图如图6所示。图6中3组数据文件Data1～Data3的记录时间长度分别为622 s、974 s、651 s，3组数据为水下5 m单水听器接收的某中型螺旋桨飞机水面上空飞行时的飞行噪声信号，飞机匀速直线往返飞行，飞行高度约为150 m，数据记录采样频率为10 kHz.

从时频谱图中可以同时观察信号在时域和频域上的信息，包括信号的频谱特征以及频率随时间的变化。以实测信号Data1为例，分析图6所示时频谱图中在200 s左右目标出现的时刻，纵轴所示信号的能量急剧增强并在200 Hz上下伴有明显的线谱特征，线谱之间存在谐频特征，因此对该实测信号进行谐波检测是完全可行的。

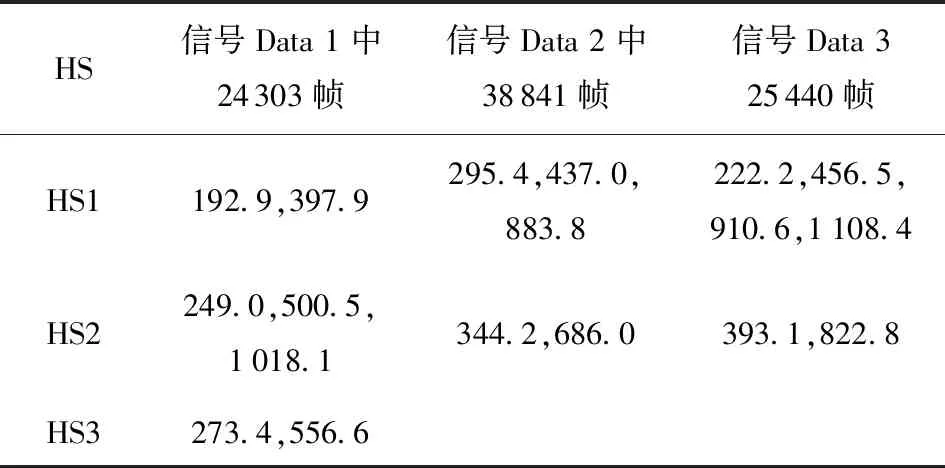
对实测信号做预处理后进行谐波检测，每次取1 024个点作为1个数据段，将其分为互相重叠50%的子段，加窗作快速傅里叶变换(FFT)，所得功率谱的频率分辨率约为1 Hz. 选取子段中前10个最大的谱峰进一步作HS检测，若出现3个以上谐波即1个HS时，则认为成功检测到目标信号HS. 这里选取实测信号Data1的子段信号，检测到的目标信号谐波关系如图7所示，具有谐波关系的线谱在图中用圆点示出。对3次实测信号Data1～Data3结合自适应门限调节因子作谐波检测，发现目标时检测到的HS如表1所示。

Tab.1 Harmonic set of measured signals Hz

3.2 实测信号检测结果分析

以第1次实测信号Data1为例进行分析，如表1所示，HS检测的线谱频点有：192.9、249.0、273.4、397.9、500.5、556.6、1 018.1，其中存在谐波关系的HS有{192.9，397.9}，{249.0，500.5，1 018.1}，{273.4，556.6}。在实测过程中存在船舶噪声干扰，如图8所示为采集的一段无飞机的纯船舶噪声段，由其频谱分析可知此船噪声主要集中在245 Hz左右，对其单独进行HS检测，检测到的HS{244,488,967}与Data1中的HS{249.0,500.5,1 018.1}基本一致，从而目标检测时可用此HS排除船舶噪声的干扰，并以此检测识别飞机目标。

由于实测信号受风浪、船只等外界因素的影响，对3次实测信号检测到的谐波线谱不完全相同。但由于是同一架飞机，HS检测所得谐波基频相差不大，表明谐波检测算法在不断变化的环境条件下仍能保持稳定的检测性能。

根据图4的检测算法原理，若某帧信号检测的线谱间不存在谐波关系，则寻找线谱中最强的谱峰，与DT进行比较来判断有无目标，若大于DT则输出H1，否则判断为H0，继续观测。为了保证检测效果，若连续检测10次都判断为H1，则认为发现目标，其中DT为发现目标前最后一帧信号计算所得的门限值，检测概率的计算公式为

(10)

使用该方法进行检测的结果如图9所示，根据图9的检测结果可以获得实测信号的相关预警信息，在检测到目标后即发出预警信息，同时若检测到HS，则可利用HS的基频对目标进行辅助识别，判断目标是否为飞机。按照实验中该型号飞机的正常巡航速度v=36 m/s计算，预警距离为

(11)

式中：t1为发现目标的时刻；t2为目标过顶的时刻。

由(11)式可得预警距离如表2所示。从图9和表2可知，从发现目标开始直至目标到达最靠近点(CPA)[17]，可以保持较远的预警距离，并在检测到目标后保持较高的检测概率。

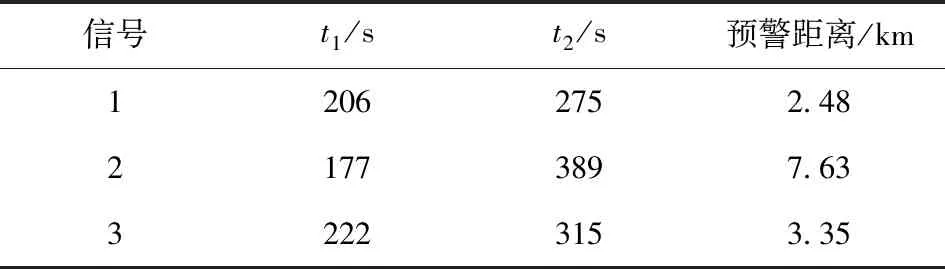
表2 实测信号预警信息

4 结论

本文针对螺旋桨飞机的水下声探测，根据其辐射噪声信号的谐波特性，提出了HS检测与最强谱线检测相结合的检测算法；采用门限调节因子α自适应地调整DT，用实测信号进行了目标检测试验验证。主要得出以下结论：

1) 螺旋桨飞机噪声信号具有谐波特性，通过基于抛物方程的RAMGEO模型进行仿真计算表明，可将声源空气- 水跨界传播问题转换为水下声传播问题，从而按照等效源理论进行空中目标的水下探测。

2) 在HS检测过程中，线谱检测是至关重要的一个环节，可以通过选取兼顾谱峰左右边界、峰宽和峰高等特征来提取线谱。

3) 若某帧信号检测的线谱间不存在谐波关系，则可寻找线谱中最强的谱峰，从而利用基于自适应门限调节因子α的最强谱线检测方法增强HS检测方法的稳定性，有效提高目标的检测距离。