从一道习题引发的矛盾谈几何教学
梁姣
不久前,笔者上了一堂初三几何复习课。这堂课的教学重点是巩固“点、直线与圆的位置关系”。对点与圆的三种位置关系、直线与圆的三种位置关系,初三的每一个孩子都应如数家珍,也能较熟练地说出判断点与圆的位置可由点到圆心的距离跟半径的大小比较来确定,而要证明直线与圆相切则应该同时具备“直线过半径的外端点,直线垂直于此半径”两个条件。所以在孩子们的心目中,判断点与圆的位置关系或判断直线与圆的位置关系的相关题型都是基础题。
于是我摆出了一道“龙门阵”:
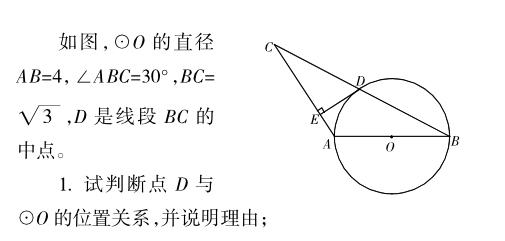
2.过点D作DE彝AC,垂足为点E,求证:直线DE是已O的切线。
教师要求每个孩子看题时务必将已知条件标到图中,至少读题1分钟后再开始动笔写。时间一到,不少孩子就迫不及待地“洋洋洒洒”起来。
部分同学这样写:

從教室里走了一圈,我发现此类同学不在少数。于是,通过展台,我将一个书写工整漂亮的学生的证明过程投影到屏幕上,让大家一起来点评。看到的是一个个欣赏与认同的眼神,“有人需要补充或指正吗?”我足足沉默了两分钟,无疑是肯定地告诉了他们这个方法是错的。经过这“一瓢冷水”,终于有人陆续发现了破绽,于是质疑声起:“为什么∠ADB=90毅呢?”仍有些孩子据理力争:“直径所对的圆周角为90毅呀!”“既然∠ADB是圆周角,那不就是你们事先知道了点D在圆周上喽?那还要证明点D在圆周上吗?”如此一辩,其他人如梦初醒。“嗯!是不对劲!”“是啊,矛盾!矛盾!”“的确错了!”……我趁热打铁:“如何证明才行呢?看谁最聪明,先想出办法来?”果然,不出5分钟,就相继有人攻破了我的这道“龙门阵”,而且还想出了好几种方法来:如过点O作OH彝BD于点H,通过勾股定理求出BH的长,再求出OD的长,得出OD是等于半径的。又如设⊙O与BC交于点M,连接AM,可根据条件求出BM的长,从而得出BM越BD,即点M与点D重合,由点M在已O上得点D在已O上……,孩子们的思维一下子活跃起来。
突破了第1问再求解第2问,孩子们很自然地关注到一个事实:确定了点D在已O上后,OD就确定是半径,剩余要证明的就是OD与DE的垂直关系。这对他们来说可是轻车熟路,便一气呵成了!
趁热打铁,我给出了一道变式题,此时,大部分孩子都顺利过关,一个个兴高采烈。我分享着他们成功地喜悦,也为他们由衷地点赞。
本节课的教学工作圆满完成,达到了我为他们设置这一道“龙门阵”的预期效果,可以说是收获颇丰,反思教学过程,笔者也有了新的感受。

几何证明是逻辑思维的培养与训练的重要途径,是由题目给出的已知条件,根据所学知识与原理,一步步推导出所要结论的过程。整个步骤是环环相扣的,不能脱节,忌讳“想当然”,更不能前后矛盾或脱离事实。因此,我们可以设置适当的问题,给学生制造一些思维上的障碍,从而有效地引发争论,包括自己思考过程中的争论,以及与同学之间不同意见的争论,把他们潜在的一些问题摆到了明面上,激发学生进行辨与辩,进而对相关知识有了更明确的认识。这个发现问题→分析问题→解决问题的过程,能不断提升学生的学习能力。
学生很多时候犯的错误都是因为粗心。细心是一种好的习惯,也是一种优秀的品质。虽然没人保证绝对不犯粗心这个毛病,但我们应该学会从错误中分析原因,汲取教训,这样才能想办法去克服,避免重蹈覆辙。如果一开始我就将这道题的易错点告诉学生,他们便失去了一次犯错的机会,也不会留下这么深刻的印象,更不会吸取教训。所以说,适当地制造机会让学生犯错,不失为增强他们“免疫力”的一种有效途径,可以达到事半功倍的效果。
事实证明,经历了一些必要的坎坷,孩子们在往后的数学证明与求解时,学会了多留个心眼,养成了追根溯源的习惯,思维更严谨,解题能力、学习能力也得到了逐步提升,数学素养慢慢提升。
(作者单位:长沙县百熙实验学校)

