基于ADMM算法的航空发动机模型预测控制

单睿斌，李秋红，何凤林，冯海龙，管庭筠

（南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京210016）

模型预测控制（Model Predictive Control，MPC）具有显式处理航空发动机工作中约束的能力，可以简化航空发动机控制系统的结构，在发动机控制领域获得了广泛的关注[1-4]。MPC通过在线优化的手段获得最优控制量，因此高效的在线优化算法可以提升MPC的实时性，有助于其在航空发动机上的应用。常用于MPC的优化算法有二次规划（Quadratic Programming，QP）[5]和序列二次 规 划 （Sequential Quadratic Programming，SQP）[6]。SQP方法在每次迭代中需要计算一个QP子问题，计算量大，实时性较差；求解QP问题的方法包括内点法（Interior Point Method，IPM）和有效集方法（Active Set Method）。有效集方法每次迭代需要判定有效集操作，且无法利用MPC问题稀疏性求解，适合控制变量和约束数量较少的情况[7]；IPM在每次迭代中需要求解 Karush-Kuhn-Tucker（KKT）系统，可以利用 MPC的稀疏性加速求解，但是在迭代过程中KKT系统会改变，每次迭代需要进行矩阵分解或者求逆操作[8]，在约束多或预测时域较长的情况下计算耗时较多。

交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）于 1975年提出，在20世纪80年代获得广泛讨论[9]，其将一个大的、具有可分结构的凸优化问题分解为几个小的优化问题，降低了求解的难度和算法的复杂性。近10年来，原本用来求解变分不等式的 ADMM在优化计算中被广泛采用[10-12]。

本文通过引入辅助变量将航空发动机MPC中的QP问题转化为可分结构的优化问题，并基于ADMM算法对其进行求解，与IPM算法进行比较，验证了ADMM算法的优越性。

1 航空发动机MPC问题

航空发动机控制系统具有稳态控制、加减速控制[13]、超限保护控制[14-18]、抗执行机构积分饱和等功能。传统的发动机控制系统各功能模块通过min／max选择、切换等逻辑综合为一个整体，控制结构复杂。在MPC中，控制量通过求解一个约束最优化问题来获得，只需要一个优化控制器，就可以实现上述所有控制功能，且避免了设计过程中的保守性，因而得到了广泛的关注。

在单输入MPC中，取二次型性能指标，在采样时刻d之后的预测时域内，航空发动机MPC的目标是求解在预测时域内使性能指标J最小的燃油流量Wfb输入序列，同时满足发动机低压转子转速Nl、压气机出口静压 P3s和低压涡轮出口总温T6不超过其最大值。可表示为

式中：ref为高压转子转速指令；Nh为高压转子转速；λ为权重系数；np为预测时域的长度。

求解式（1）需要获得各个输出量和 Wfb之间的解析表达关系。在采样时刻d将发动机表示为一个线性系统为

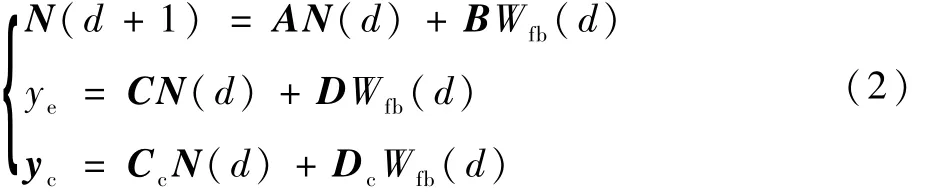
式中：N=[Nl，Nh]T为状态量；ye=Nh为被控制量；yc=[Nl，P3s，T6]T为需要限制的量；A、B、C和D为系统的系数矩阵；Cc、Dc为限制量对应的输出矩阵。

利用离散系统状态方程的响应：

可以获得输出量在预测时域np内的预测值，其预测方程为

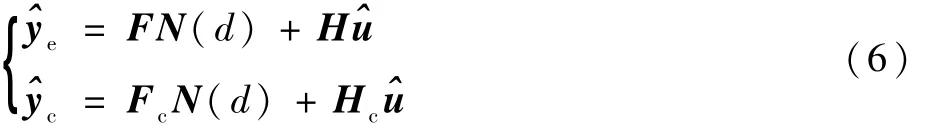
式（1）可以改写为一个带有线性不等式约束的二次规划问题：

式中：Ymax为由 Nlmax、P3smax和 T6max组成的适当维数的与对应的限制序列；Umax为由Wfbmax构成的输入限制序列。

通过求解QP问题式（7），可以获得满足约束条件下，使性能指标最小的最优控制输入序列

为了实现闭环非线性控制，将序列的第一个值Wfb（d+1）作为发动机所需燃油输入量，然后在d+1采样时刻，根据发动机的状态变化重复进行线性化，构造QP问题，求解输入序列。这样在每个采样周期求解的是一个线性MPC问题，但在整个时域内是一个非线性MPC问题。

MPC通过迭代进行优化搜索来获得最优的控制序列，如果迭代过程耗时较多将限制算法的应用。ADMM算法具有对偶上升法的可分解性以及乘子法的全局收敛性，近年来得到了大量关注，由于其所需计算量小、算法结构简单，本文将其用于求解航空发动机MPC中的优化问题。

2 交替方向乘子法

ADMM算法可用于求解形如的约束规划问题。式中：x∈Rn，z∈Rm为待优化变量；f（x）+g（z）为待优化的目标函数；L∈Rp×n，M∈Rp×m，c∈Rp，Lx+Mz=c为问题需满足的线性等式约束。

通过乘子法，引入对偶变量y，构造增广拉格朗日函数：

式中：ρ＞0为惩罚参数。

ADMM迭代过程与对偶上升法和乘子法相似，包含3部分：原始变量x的迭代更新、原始变量z的迭代更新和对偶变量y的更新过程，更新策略为[19]

可以看出，在 ADMM算法中，原始变量 x和原始变量z的迭代更新是一个交替进行的过程，每个求解过程只需求解部分变量，降低了求解规模。

3 航空发动机MPC的ADMM算法实现

将式（7）所描述航空发动机MPC中的QP问题简写为

式中：P=HTH+λI为正定对称矩阵；

为应用ADMM算法，首先添加辅助变量，将式（11）改写为等式约束的形式：

由于式（12）所描述的QP问题不具有可分形式，不能直接采用ADMM算法进行求解。为此将x和z视作为一个整体变量（x，z），引入辅助变量约束）=（x，z），式（12）可以写为

式中：f2（x，z）为集合的指示函数集合的指示函数。

引入对偶变量 （w，y），根据式（10），可以得到求解式（13）的ADMM迭代过程为[20]

式中：σ为惩罚系数。

式（14）表示辅助变量的更新过程，是一个等式约束的QP问题，其一阶最优性条件（KKT条件）为

式中：v（k+1）为拉格朗日乘子。消去，可以获得

式（18）的系数矩阵称作KKT矩阵，该矩阵是一个列满秩的对称矩阵，因此方程具有唯一解。观察式（18），KKT矩阵的结构只和式（11）与参数ρ相关，在迭代过程中是不变的。~x（k+1）与 v（k+1）可以通过式（20）获得：

为了加速算法收敛，根据文献[12]，加入松弛因子 α∈[1，2]，迭代过程式（22）和式（16）变成

根据QP问题的一阶最优性条件，定义QP问题式（12）的原始残差rprim和对偶残差rdual：

根据2个残差给出收敛判定准则：

一般取εrel=10-3，εabs根据需要精度选择。

使用ADMM算法还需要一个初始值，由于MPC问题的特殊性，可以将d-1时刻的最优解（x*（d-1），y*（d-1））作为 d时刻的算法初始值，即

因此可以获得航空发动机MPC求解控制输入Wfb的流程：

1）获得发动机采样时刻 d的状态和状态方程。

2）以二次型性能指标和约束，根据状态方程建立问题式（7）。

3）将问题式（7）改写为适合用 ADMM算法的形式（13）。

4）根据式（29），将 d-1时刻得到最优解作为d时刻问题求解的初始值。

5）根据迭代过程式（19）、式（20）、式（23）和式（24）计算并更新各个变量。

6）根据原始残差rprim和对偶残差rdual判断迭代过程是否满足精度要求。若满足，则终止迭代，将获得的最优解的第一项作为所需Wfb送入发动机，进入步骤7）；若没有，进入步骤4），直至达到最大迭代次数。

7）进入采样时刻d+1，重复步骤1）。

4 仿 真

4.1 控制结构

图1为航空发动机MPC系统结构，主要包括模型预测控制器和发动机模型。MPC根据输入的参考指令ref，使用第3节所述流程求解控制量Wfb；实时非线性模型用于获得预测模型，并且通过模型的输出与真实测量值之差作为反馈校正。实时非线性模型为平衡流形展开模型[21]，离线得到，其输入为 Wfb，状态量为 Nl和 Nh，输出为 Nl、Nh、P3s和T6，调度参数为发动机进口温度 T2和Nh；基于发动机进口条件和当前工作转速，以此平衡流形展开模型获得预测模型。使用部件级模型作为真实发动机，以ADMM算法对控制量进行迭代寻优。

平衡流形展开模型通过实验数据离线计算所得，其输出与发动机传感器输出存在一定的误差，使得预测模型也存在误差，为了满足控制精度的要求，需要对预测方程的输出进行修正。

在 d时刻，预测模型的输出 Nl、Nh、P3s和 T6为 ym（d），真实发动机传感器输出为 ys（d），二者的误差为 e（d）=ys（d）-ym（d），则未来时刻模型的输出可以校正为

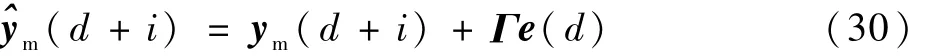
图1 航空发动机MPC系统结构Fig.1 Aircraft engine MPC system structure

4.2 仿真结果

使用MATLAB进行仿真，MPC算法由 MATLAB实现，模拟真实发动机的部件级模型使用VC++开发，并且通过MEX方法在MATLAB中调用。

指令跟踪的目的是让发动机Nh跟随参考指令ref的变化，MPC的性能指标J的第一部分即是指令跟踪的误差（见式（1））。通过在高度 H=0 km，Ma=0，在发动机慢车以上给定发动机Nh指令，使用图1所示的控制结构，进行Nh闭环控制。

ADMM算法最大迭代次数为500次，收敛准则为εabs=1×10-5；控制器预测时域长度 np=2，权重系数λ=700。Nh响应过程、相对跟踪误差、Wfb、T6和P3s的响应过程如图2所示，数据均经过归一化处理。

图2（a）为Nh在给定指令下的响应过程，从图中可以看出，在仿真时间里，使用ADMM算法的航空发动机MPC均能使 Nh跟随指令变化。图2（b）为 Nh与 ref的相对误差，从图中可以看出，相对误差在Nh稳定时接近0，满足控制所需精度，表明ADMM算法作为在线优化算法可以满足控制器所需精度。

图2（c）为控制器计算所得的 Wfb输入曲线，图 2（d）和图 2（e）为 T6和 P3s的响应曲线。在仿真中，T6的响应速度最快，跟随 Wfb的输入变化；P3s的响应速度较 Nh快，比 T6略慢一些；Nh的响应速度最慢，这是由于转子动力学特性是所建立的部件级模型的主要动态特性，其惯性较大；由于建模中忽略了热惯性，T6紧跟Wfb变化；P3s受转子转速和燃气流量的共同作用，因此响应速度介于二者之间。观察到在仿真过程中，其在温度和压力较低区域有明显的超调。因为发动机是一个非线性系统，其动态特性随转速变化而变化，因此在仿真权重系数不变的情况下，低转速区有超调，而高转速没有。

为了验证基于ADMM算法的MPC对于发动机约束的处理能力，将T6限制适当调小，使发动机在仿真中能触及 T6限制。图3（a）为 T6将限制调小到0.87时 Nh阶跃的响应，图3（b）为 T6响应。可以看出，由于限制的存在，Nh不能跟踪给定的指令，而T6达到限制值，并且没有明显的超调。仿真表明了基于ADMM算法的MPC良好的约束处理能力，采用MPC可以取消超限保护控制回路。

为了验证ADMM算法在实时性方面的优势，使用文献[22]中所述IPM算法作为对比算法，在H=0 km，Ma=0，慢车以上转速，给定不同的阶跃幅值ΔNh和预测时域np，进行6 s的阶跃响应仿真，记录使用2种算法平均单步仿真耗时并进行对比。

图2 基于ADMM算法的航空发动机MPC响应Fig.2 Response of aircraft engine MPC based on ADMM

表1中给出了10个仿真过程中转速阶跃幅值ΔNh及预测时域设置。表2是在这些设置情况下使用IPM完成一次控制序列优化计算所需平均时间和使用ADMM所需时间。

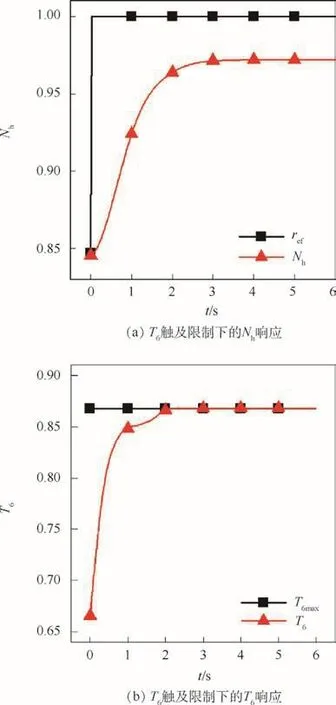
图3 T6触及限制下MPC仿真Fig.3 MPC simulation with T6 hitting limit

表1 仿真参数Tab1e 1 Simu1ation parameters

从表2中可以看出，无论ΔNh是较大还是较小的动态响应，使用ADMM的仿真耗时均低于使用IPM的仿真。这是由于ADMM算法在迭代过程中，在给定罚参数不变的情况下，KKT系数矩阵不变，因此在每次迭代过程中不必重复计算KKT矩阵的逆矩阵或分解，减少了计算量；而IPM算法在每次迭代过程中需要调整KKT矩阵，在每次迭代求解中都需要进行KKT矩阵求逆或者矩阵分解操作。假设求解需要M次迭代，矩阵分解耗时为tf，KKT系统求解回代耗时 tb，ADMM算法求解需要时间为 tf+Mtb，而 IPM算法耗时为M（tf+tb），M为求解迭代次数。

预测时域np可以表示MPC滚动优化问题的规模大小。np越大，则待求解的燃油序列维数越大，需求解的QP问题中的不等式约束矩阵和系数矩阵的维数也越大，增加了求解的计算量。

预测时域的增大可以改善航空发动机MPC的性能。图4为在H=0km，Ma=0，慢车以上转速，给定阶跃幅值 ΔNh=0.18，改变 MPC的预测时域np，得到的完成一次控制序列优化所需平均时间t与预测时域 np的关系。随着 np的增加，QP的规模增加，构成的KKT系数矩阵的维数也增加，求解 KKT方程的耗时增加。仿真结果表明，使用IPM算法的仿真耗时增加随np增加更为剧烈，而使用ADMM算法的仿真耗时增加幅度较小，证实了本文分析的合理性，表明了ADMM算法在航空发动机MPC中有比IPM更好的实时性。

表2 两种算法完成一次控制序列优化所需时间对比Tab1e 2 Time consumption comparison of two methods in finishing one-time contro1 sequence optimization

图4 控制序列优化所需平均时间与预测时域的关系Fig.4 Average time consumption for control sequence optimization vs predictive horizon

5 结 论

ADMM算法在航空发动机MPC的滚动优化中具有良好的应用前景。

1）在指令跟踪控制中，Nh与指令的相对跟踪误差均为0；表明ADMM可以满足发动机指令跟踪和约束管理的精度要求。

2）ADMM算法每次迭代过程只需计算一次矩阵分解，与IPM相比，计算量大大降低，实时性得到了很大的提高。

3）ADMM算法相对IPM有更好的计算耗时稳定性。在10组仿真测试中，预测时域从2增加到14，使用IPM算法的单次仿真耗时从10.67 ms增加到224.1 ms，扩大了20多倍；而ADMM算法从3.67 ms增加到15.53 ms，扩大不足5倍。