自适应非奇异快速终端滑模固定时间收敛制导律

赵国荣，李晓宝，刘帅，韩旭

（1.海军航空大学 参谋部，烟台264001； 2.海军航空大学 岸防兵学院，烟台264001）

使用导弹对敌方目标进行有效地打击是现代战争中的主要作战手段。导弹末制导律的设计除了要求导弹能够准确地命中目标，还要满足特定的终端攻击角度要求，以实现对目标的最大摧毁，因此，带有攻击角度约束的末制导律研究一直以来都是热点问题[1]。多年来，比例导引律及其变化形式因其简单高效的特点得到了广泛的应用[2]，然而针对高机动能力的目标，比例导引律很难满足期望的制导要求[3]。针对高机动目标的拦截问题，近年来基于最优控制、非线性控制等现代控制理论的制导律设计开始得到深入研究，如最优控制制导律[4]、微分对策制导律[5]和滑模制导律[6]。

滑模控制由于对系统不确定性和外界干扰具有较强的鲁棒性，在制导律设计中取得了一系列研究成果。文献[7]提出了一种带有落角约束滑模制导律，设计了一个线性滑模面使得视线角收敛到期望值，然而其收敛时间是趋于无穷的。终端滑模控制通过引入非线性滑模面，确保了系统状态能够在有限时间内收敛，对于高机动目标的拦截，导弹末制导时间通常很短，因此采用终端滑模控制方法针对机动目标进行制导律设计具有十分重要的意义[8-11]。文献[8]在制导律设计中引入了传统的终端滑模面，但制导指令中因为存在负指数项而导致奇异问题发生。为此，文献[9]设计了一种非奇异终端滑模面，文献[10]在研究考虑攻击角度约束的制导律时通过设计一种积分滑模面解决了奇异性问题。制导系统的状态量在远离平衡点时收敛速率较慢，文献[11]为此提出了一种非奇异快速终端滑模控制方法。

采用有限时间收敛终端滑模控制得到的系统状态收敛时间依赖于系统的初始条件，为此，文献[12]提出了固定时间收敛的概念。固定时间收敛理论可以使系统状态在收敛时得到一个不依赖于系统初始条件的收敛时间上界。然而，传统的终端滑模固定时间收敛控制依然存在奇异性问题，因此文献[13-14]针对一类非线性系统分别设计了固定时间收敛非奇异终端滑模面。文献[15]采用转换滑模面的形式进一步提出了一种非奇异快速终端滑模固定时间收敛的控制方法，并且用于制导律的设计。

在研究拦截机动目标的末制导问题时，通常需要知道目标的机动信息，然而目标的机动在实际情况中多数是不可知的。文献[10，16]通过假设目标机动存在已知的上界来进行制导律设计，然而目标机动的上界通常也很难测量得到。自适应控制由于其具有不需要知道外部扰动任何信息的优点，可以有效解决目标机动的问题。文献[9，11，17]提出了自适应非奇异终端滑模制导律的设计方法，在设计过程中目标机动的上界不需要预先已知。

末制导过程中导弹和目标初始时刻的具体状态大多事先不可知，采用固定时间收敛控制方法进行制导律设计时，系统状态的收敛时间上界是一个独立于初始条件的固定值，因此设计的制导律具有更广的适用范围和更高的制导性能。针对机动目标的拦截问题，本文在考虑攻击角度约束的情况下，提出了一种非奇异快速终端滑模固定时间收敛制导律，并且设计了一种自适应律来对目标机动上界进行估计。通过Lyapunov稳定性理论证明了制导系统能够在固定时间内收敛，并且给出了收敛时间公式。通过仿真验证了该制导律的有效性，并且与其他现有制导律进行对比，分析了该制导律的制导性能。

本文的研究工作具有以下创新点：

1）设计了一种新型的终端滑模固定时间收敛制导律，不仅能够使得导弹以期望的攻击角度命中目标，而且制导系统的弹目视线（Line of Sight，LOS）角和 LOS角速率能够在固定时间内收敛，该收敛时间不依赖于制导系统的初始条件，可以通过调节制导律中的参数而被预先设定。

2）设计了一种新型的固定时间收敛非奇异快速终端滑模面，该滑模面具有与现有有限时间收敛非奇异终端滑模面类似的形式，从而避免了奇异性问题，同时根据滑模面、系统状态与平衡点的距离，合理调整滑模面与LOS角跟踪误差的趋近律指数，从而提高了制导系统状态的收敛速率。

3）设计了一种自适应律对目标机动的上界进行估计，使得制导律的设计无需任何目标机动的信息，增强了制导系统对未知干扰的鲁棒性。

1 基础知识

1.1 问题描述

导弹末制导的运动关系如图1所示。假定导弹和目标的速度VM和VT恒定，aM和aT分别为导弹和目标的法向加速度，r和q分别为导弹和目标之间的相对距离和 LOS角，γM和 γT分别为导弹和目标的航迹角。制导系统的运动学关系可表示为

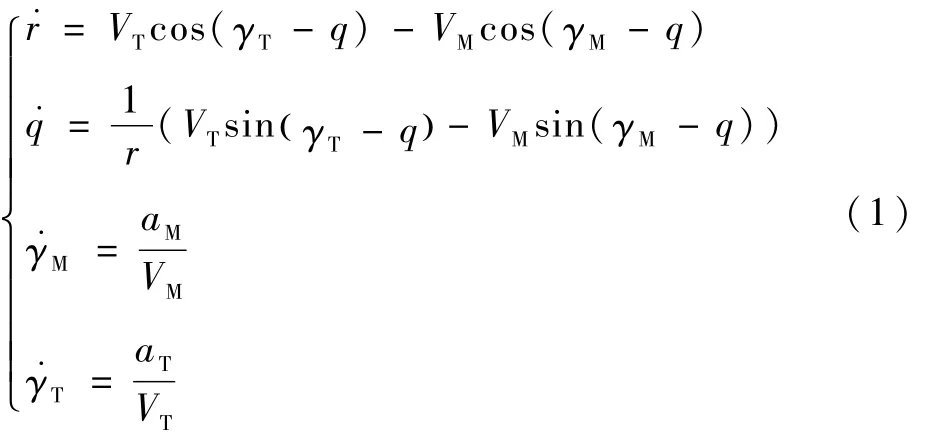
导弹的终端攻击角度θimp表示为导弹成功拦截目标时其速度之间的夹角，若 γMf和 γTf分别为导弹和目标的终端航迹角，可知 θimp=γTf-γMf。导弹终端攻击角度θimp与终端LOS角qf存在着一一对应关系[9]。

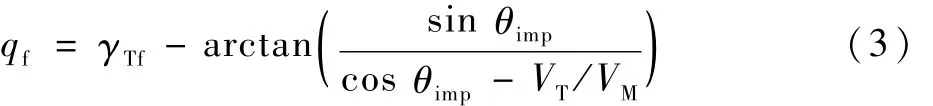
因此，导弹末制导终端攻击角度 θimp约束可以转化为终端LOS角qf约束问题。

假设qd为期望的末制导终端 LOS角，定义LOS角跟踪误差为x1=q-qd，LOS角速率为x2=。由式（1）和式（2）可以得到

图1 导弹和目标之间的运动关系Fig.1 Missile and target engagement geometry

式中：d=aTcos（γT-q）。

假设1 d可看作为由目标机动而引起的外部干扰，假设Δ≥0为一常数，表示为目标机动aT最大值，可知≤Δ。

通过末制导律设计使得LOS角跟踪误差x1及LOS角速率x2能够在固定时间之内收敛到原点，那么导弹便能够以期望的终端LOS角qd精确命中目标。

1.2 基本定义和相关引理

定义1[12]考虑如下非线性系统：

式中：x∈Rn；F（x，t）：U×R+→Rn是连续的，U为一个包含x=0的开区间，且 F（0，t）=0。若任意给定初始时间t0和初始状态x0∈U，都存在时刻 T（x0），使系统式（5）的每一个解 x（t）=x（t；t0，x0）满足如下关系：

则系统式（5）的平衡点x=0是有限时间稳定的。此外，若收敛时间 T（x0）是有界的，即对任意的x0∈Rn，都存在一个 Tmax＞0，使得 T（x0）＜Tmax，则系统式（5）的平衡点x=0是固定时间稳定的。

引理1 考虑一类非线性系统：

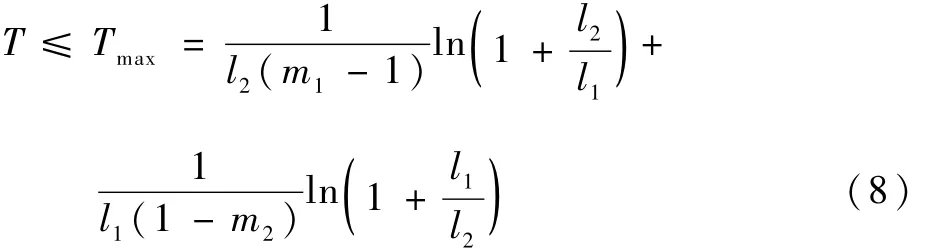
证明 系统式（7）可被改写为

因此，系统式（7）的收敛时间上界Tmax满足：

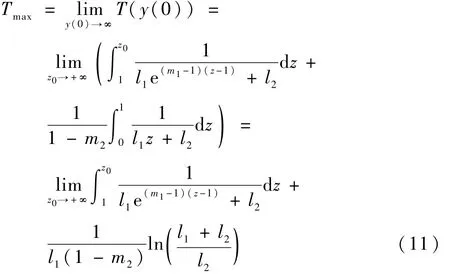
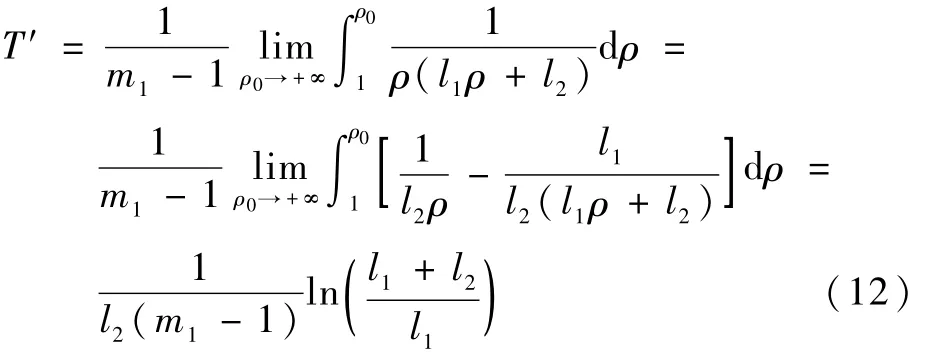
即

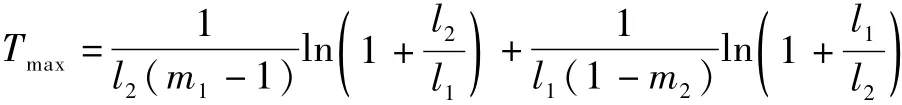
证毕

注1 文献[14]提出了传统的固定时间收敛系统˙y=-l1sigm1y-l2sigm2y，并给出了收敛时间上界：

社会实践具有良好的教育功能,对实现高校德育目标起着关键作用。社会实践的开放性需要大学生独立面对和解决问题且在实践中积极地思考、解决问题,为创新精神的培养奠定基础。通过这种方式,提高了大学生对国情、城市状况、公共条件以及社会条件的认识,促使他们将个人与社会理想结合起来,从而实现个体与社会价值观的统一。

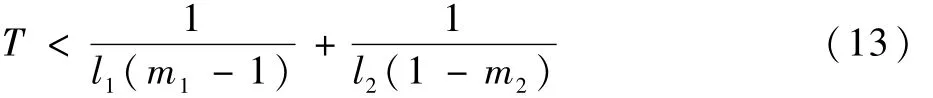
式中：l1＞0，l2＞0，m1＞1，0＜m2＜1。文献[15]进一步提出了快速固定时间收敛系统˙y=-l1yκ-l2yp2／q2，并给出了收敛时间上界：

式中：q1、p1、p2、q2为正奇数，并且满足 p1＜q1，p2＜q2。因为，所以本文给出的固定时间收敛系统与文献[14-15]相比，收敛速率更快。

2 制导律设计

2.1 新型滑模面的构造

考虑一类二阶非线性系统，文献[18]构造了一种固定时间收敛的终端滑模面：

式中：l1＞0，l2＞0，m1＞1，0＜m2＜1。

对滑模面式（15）求导可得

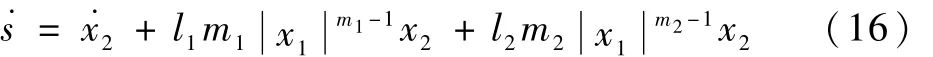
式（16）中，当 x1=0，x2≠0时，幂次项会引发奇异性问题。为避免奇异现象，本文构造了一种新型的固定时间收敛非奇异快速终端滑模面：

注2 文献[9]研究有限时间收敛制导律时设计了一种非奇异终端滑模面：

1转化为与式（18）类似的形式从而避免了奇异问题的发生。

2.2 稳定性分析

定理1 对于制导系统式（4），若采用本文构造的滑模面式（17），设计制导指令 aM为如下形式：

式中：σ≥1，α1＞0，α2＞0，β1＞1，0＜β2＜1为目标机动上界 Δ的自适应估计值，设计自适应律为

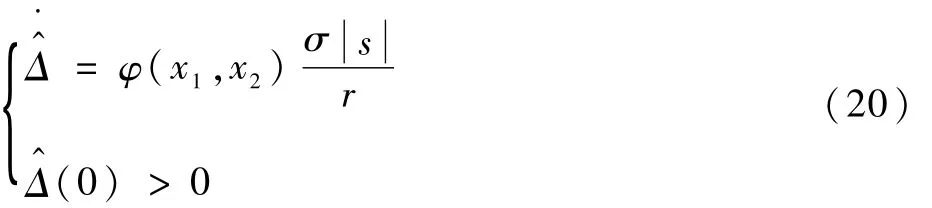
式中：τ为一个小于1的正常数。

则下面的结论成立：

2）滑模变量s在时间Ts内收敛到0。

3）制导系统式（4）的状态变量 x1、x2在时间T内收敛到于0。

其中：Ts＜T1+ε（t），T＜T1+T2+ε（t），T1=ε（t）为一个与τ相关的小时间函数。

证明 1）考虑Lyapunov函数：

根据式（17）、式（19）和式（20）可知，Lyapunov函数V的导数为

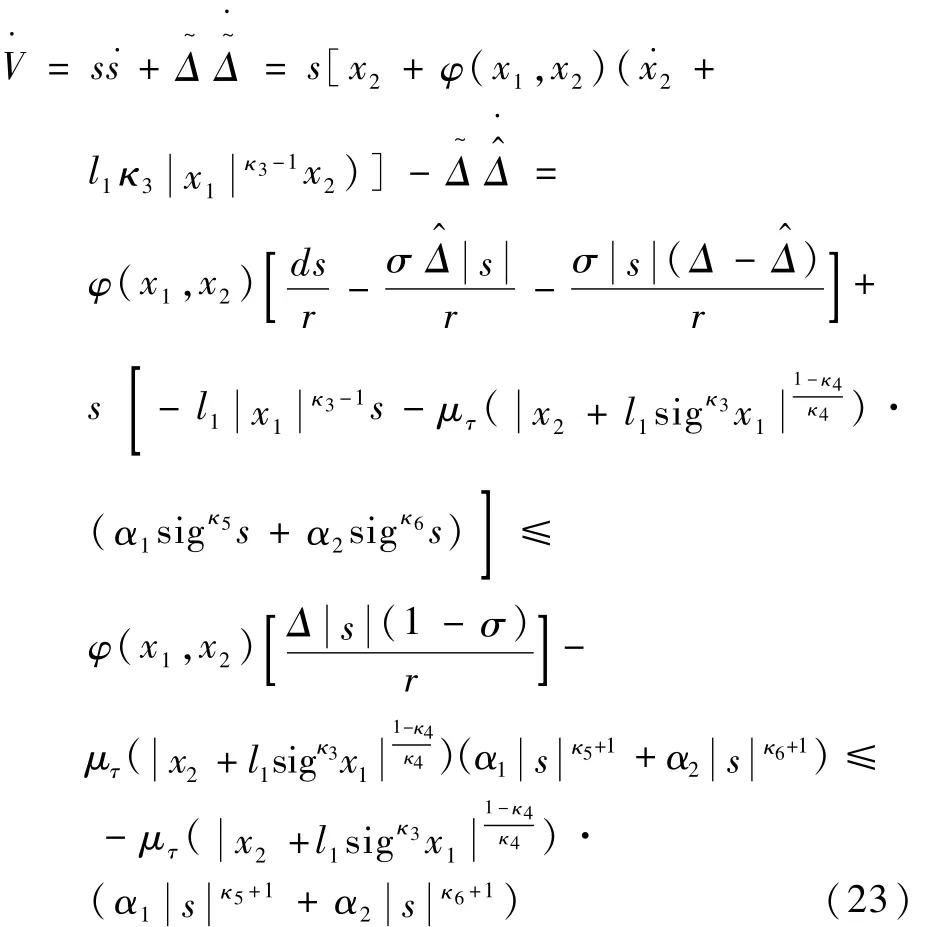
2）考虑Lyapunov函数：

对 V1求导，代入式（17）和式（19）可得

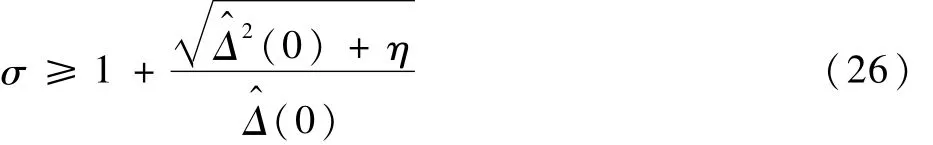
式中：η≥0为一任意小的常数。那么

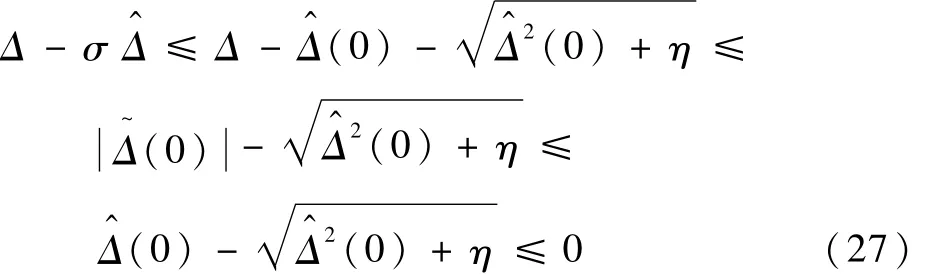
因此，可以得到

当系统状态（x1，x2）在区域Ω1时，≤，系统在固定时间T1内到达滑模面 s或者进入区域 Ω2。当系统状态（x1，x2）在区域 Ω2时，因为 τ＜1，此时可知 κ4=m4。当g=0时，则有

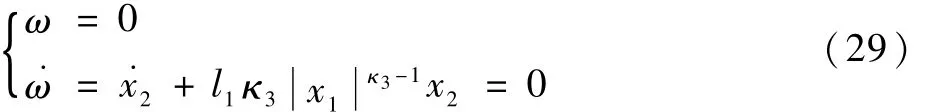
此时制导指令aM为

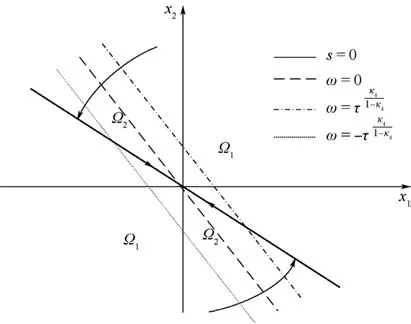
图2 制导系统变量的收敛过程Fig.2 Convergence process of guidance system variable

3）当制导系统式（4）状态量 x1、x2到达滑模面式（17）时，由 s=0可知

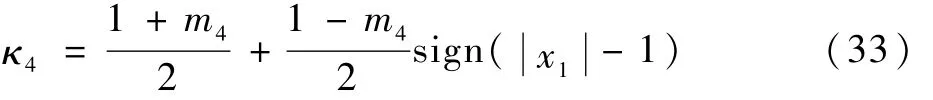
由式（32）及引理 1可知，制导系统式（4）的状态变量x1、x2将在时间T内收敛到于0。 证毕

注3 滑模面式（17）中 κ4的设计形式与引理1中的形式并不相同，这是为了保证滑模面s始终是连续的，并且当 s=0时，由定理1中的证明过程3）可知，式（17）中设计的 κ4可以转化为，这与引理 1中的κ2的形式相同，因此κ4的设计并不会影响系统状态x1、x2在滑模面上固定时间收敛的特性。

注4 有限时间 ε（t）虽然不能被精确地求出，但是可以被近似地估计。如图2所示，当制导系统式（4）的状态变量 x1、x2穿越区域 Ω2时，对于一个充分小的常数τ，在区域Ω2内因为0＜g≤τ，因此可近似认为ω=0，并且由式（17）可知 s=x1。此外，根据式（31）可得

对式（34）两边积分得

求解式（35）可得

因此，可知 τ取值较小时，ε（t）也会变得很小，可以忽略不计。

因为符号函数 sign（s）的存在可能会引起颤振，为避免振颤现象的发生，符号函数 sign（s）可采用一种Sigmoid函数近似替代：

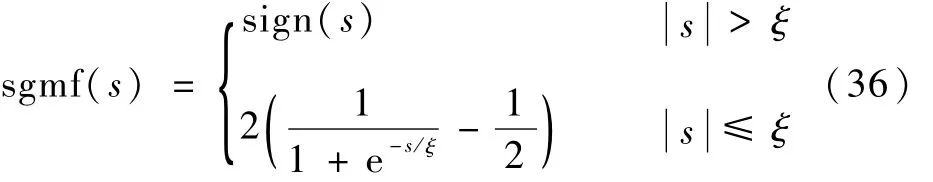
本文最终设计的带有攻击角度约束的自适应非奇异快速终端滑模固定时间收敛制导律（AFTNFTSMG）形式为

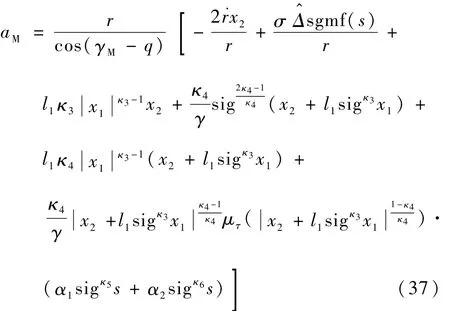
3 仿真分析

针对制导律 AFTNFTSMG进行仿真分析，参照文献[11]的仿真场景，假设导弹和目标的初始相对距离 r0=5 000 m，初始 LOS角 q0=30°，目标的初始航迹角γT0=0°，导弹和目标的速度分别为VM=600 m／s，VT=300 m／s。AFTNFTSMG中的参数取值为：l1=l2=0.5，α1=α2=2，m1=β1=9／7，m2=β2=7／9，τ=0.1，ξ=0.01，σ=2（0）=100，g=9.8 m／s2，导弹最大加速度值为 30g。根据定理1计算可得T=13.86 s。

注5 由定理1可知，T的大小完全是由AFTNFTSMG中的参数决定的，与制导系统的状态无关。固定时间T表示的是制导系统任意初始状态下收敛时间的上界，通常制导系统实际收敛时间要小于T。T的设定需要结合制导系统的具体环境。如果 T设计的太小，在某些情况下，例如初始LOS角跟踪误差x1较大时，为了达到制导系统固定时间收敛的要求，导弹必须具有较强的机动能力，但是导弹的机动能力是有限的，因此制导指令在末制导前期可能会出现饱和现象。如果T设计的太大，因为导弹末制导时间有限，可能导致导弹无法以期望的攻击角度准确命中目标。所以，需要通过调节AFTNFTSMG中的各个参数合理设置T的大小。

3.1 以不同初始航迹角拦截目标

假设目标机动 aM为：当 t≤5 s时 aM=7g；当t＞5 s时，aM=-7g。导弹拦截目标时，期望的终端LOS角 qd为 20°，导弹的初始航迹角 γM0=30°，60°，90°。针对 AFTNFTSMG进行仿真分析，结果如图3所示。

图3（a）表明，AFTNFTSMG能够使导弹在不同的初始航迹角γM0下有效地拦截目标。图3（b）的制导指令曲线表明，导弹制导指令在前期都出现了饱和现象，这是因为在末制导的前期，为满足导弹LOS角q和LOS角速率在固定时间之内收敛，通常情况下导弹需要进行高强度机动。图3（c）、（d）表明，q和˙都能够在设定的固定时间T内收敛，制导指令饱和现象的存在会使得q和实际收敛时间增大，然而因为T是制导系统在任意初始状态下的收敛时间上界，通常q和依旧能够在T内收敛。图3（e）表明，滑模面s在不同的初始航迹角γM0下都能够在q和˙q收敛之前快速收敛到0。

图3 不同初始航迹角拦截目标的仿真结果Fig.3 Simulation results of intercepting target under different initial flight path anges

3.2 以不同期望终端LOS角拦截目标

假设目标机动 aM为：当 t≤5 s时 aM=7g；当t＞5 s时，aM=-7g。导弹初始航迹角 γM0=60°，导弹拦截目标时期望的终端 LOS角 qd=20°，30°，40°。针对 AFTNFTSMG进行仿真分析，结果如图4所示。

从图 4（a）可以看出，在 AFTNFTSMG作用下，导弹能够以不同的期望终端LOS角qd精确地拦截目标。图4（b）给出了相应的制导指令曲线，其中制导指令在qd=40°时饱和时间最长，这也导致了其对应的q和收敛时间最长。图4（c）、（d）、（e）表明，在不同的期望终端 LOS角 qd要求下，q和˙q依然能够在设定的固定时间T内收敛，相应的滑模面s在q和˙收敛之前能够先收敛到0。

假设qd=20°，考虑测量噪声对制导性能的影响，在获取LOS角速率˙时加入均值为0、方差为真值1%的高斯白噪声，仿真结果如图5所示。表明由于噪声的影响，在AFTNFTSMG的作用下，˙q虽然前期产生了微弱的振颤现象，但最终依然能够保证固定时间收敛特性，同时制导指令最终也能够跟踪到不含噪声的制导指令曲线上来。

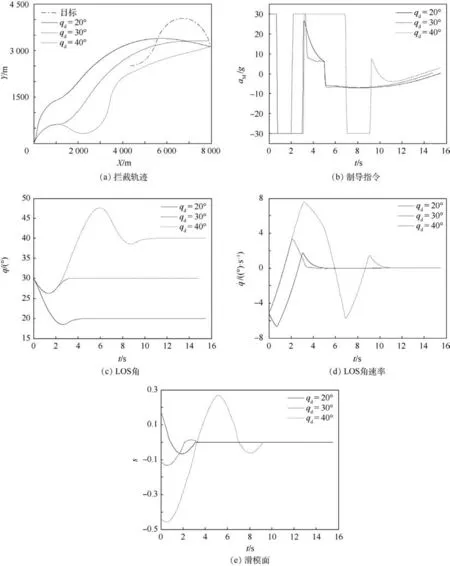
图4 不同期望终端LOS角拦截目标的仿真结果Fig.4 Simulation results of intercepting target under different desired terminal LOS angles

为进一步说明测量噪声对AFTNFTSMG制导性能的影响，对期望终端 LOS角 qd=20°，30°，40°的情况各做100次蒙特卡罗仿真，计算脱靶量和终端LOS角跟踪误差的均值和方差，结果如表1所示。可以看出，3种情况下脱靶量均值不超过0.04 m，终端LOS角跟踪误差均值小于0.02°，且方差均维持在零左右，表明在测量噪声影响下，AFTNFTSMG依然能够使制导系统保持稳定。这是因为测量噪声通常是有界的，可以和目标的机动一起看作制导系统的外部干扰，AFTNFTSMG中得益于自适应律的设计，使得制导系统对外部干扰具有较强的鲁棒性。

3.3 不同制导律仿真对比

为了全面分析AFTNFTSMG的制导效果，在仿真中与其他制导律进行对比分析。

文献[19]设计了一种非奇异终端滑模制导律（Nonsingular Terminal Sliding Mode Guidance Law，NTSMG）：

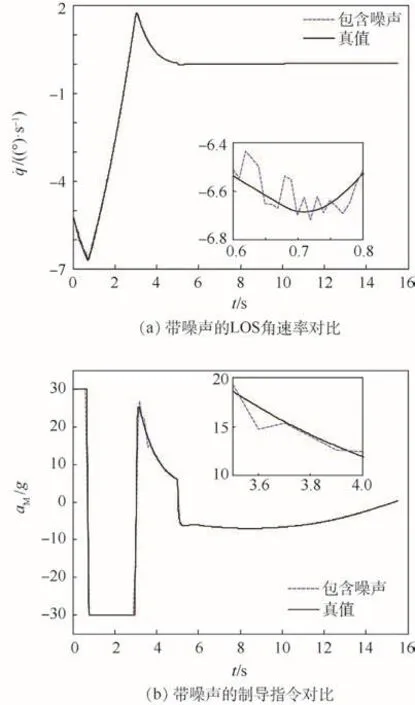
图5 测量噪声对制导性能的影响Fig.5 Influence of measurement noise on guidance performance

表1 蒙特卡罗仿真统计Tab1e 1 Simu1ation statistics of Monte Car1o

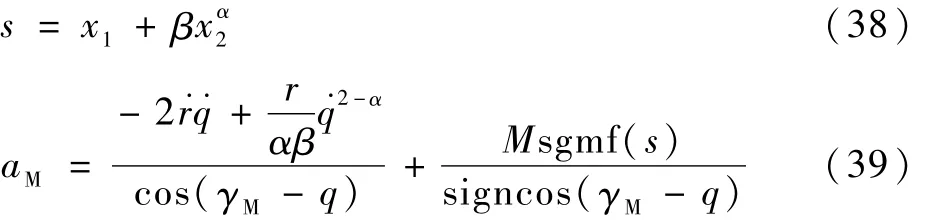
文献[15]设计了一种自适应固定时间收敛非奇异终端滑模制导律（Adaptive Fixed-Time Nonsingular Terminal Sliding Mode Guidance Law，AFTNTSMG）：

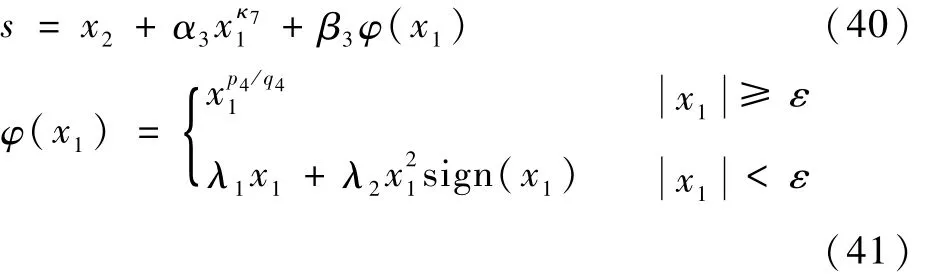
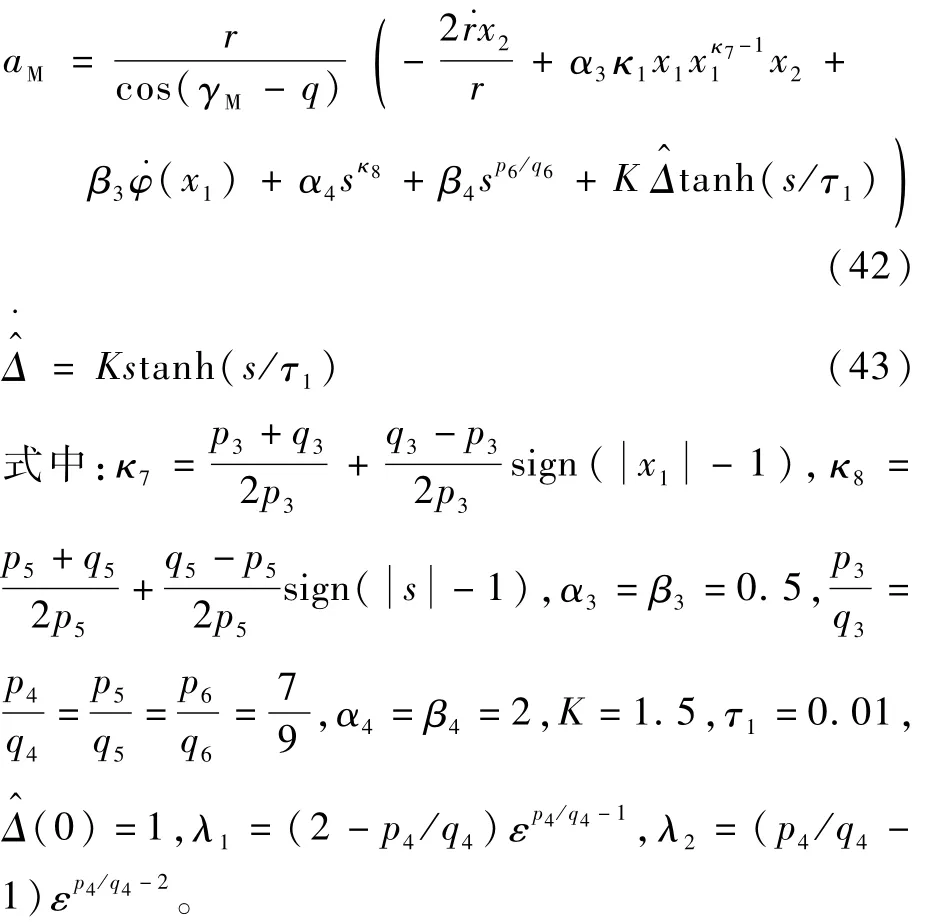
此外，为了评估导弹在末制导过程中消耗的能量大小，文献[20]给出了平均拦截加速度aME的概念，定义如下：

式中：N为总的仿真步数；aM（k）为第k步的制导指令仿真值。

假设目标采取 aM=7g cos（πt／4）进行机动，导弹初始航迹角γM0=60°，导弹拦截目标时期望的终端LOS角qd=20°，通过仿真对制导律 AFTNFTSMG、NTSMG和 AFTNTSMG的制导性能进行对比，仿真结果如图6和表2所示。

图 6（a）表明，制导律 AFTNFTSMG、NTSMG和AFTNTSMG在设定的制导场景下都能够使导弹成功地拦截目标。图 6（c）、（d）、（e）表明，在AFTNFTSMG作用下，˙q、q及滑模面s收敛速率最快，并且在AFTNFTSMG和AFTNTSMG的制导指令选取了相同参数的情况下，AFTNFTSMG使得系统状态收敛更快。由表2可以看出，导弹在NTSMG、AFTNFTSMG和 AFTNTSMG的作用下拦截时间分别为 20.616 0 s、17.157 0 s和17.496 3 s，同时导弹在AFTNFTSMG作用下的脱靶量也是最小的，仅为0.018 4 m，这说明相比其他2种制导律，AFTNFTSMG能够使得导弹具有更短的拦截时间及更高的制导精度。由注1可知，AFTNFTSMG使制导系统收敛速率比AFTNTSMG更快，同时AFTNFTSMG能够使得制导系统状态最终收敛到零，而AFTNTSMG采用滑模面转换的方法来解决奇异性问题，最终只能使得制导系统收敛到而不能收敛到零。因此，AFTNFTSMG相比AFTNTSMG收敛速率更快，拦截精度更高。图6（b）给出了3种制导律制导指令曲线，可以看出制导指令在前期都存在着饱和现象，但是 AFTNFTSMG指令曲线相较于其他2种制导律饱和时间短，并且由于自适应律的作用，AFTNFTSMG指令曲线较为平缓光滑，而NTSMG和AFTNTSMG指令曲线变化剧烈，并且NTSMG在16 s附近存在振颤现象。同时，表2中AFTNFTSMG的平均拦截加速度aME最小，这也说明采用AFTNFTSMG制导的导弹所消耗的能量是最少的。

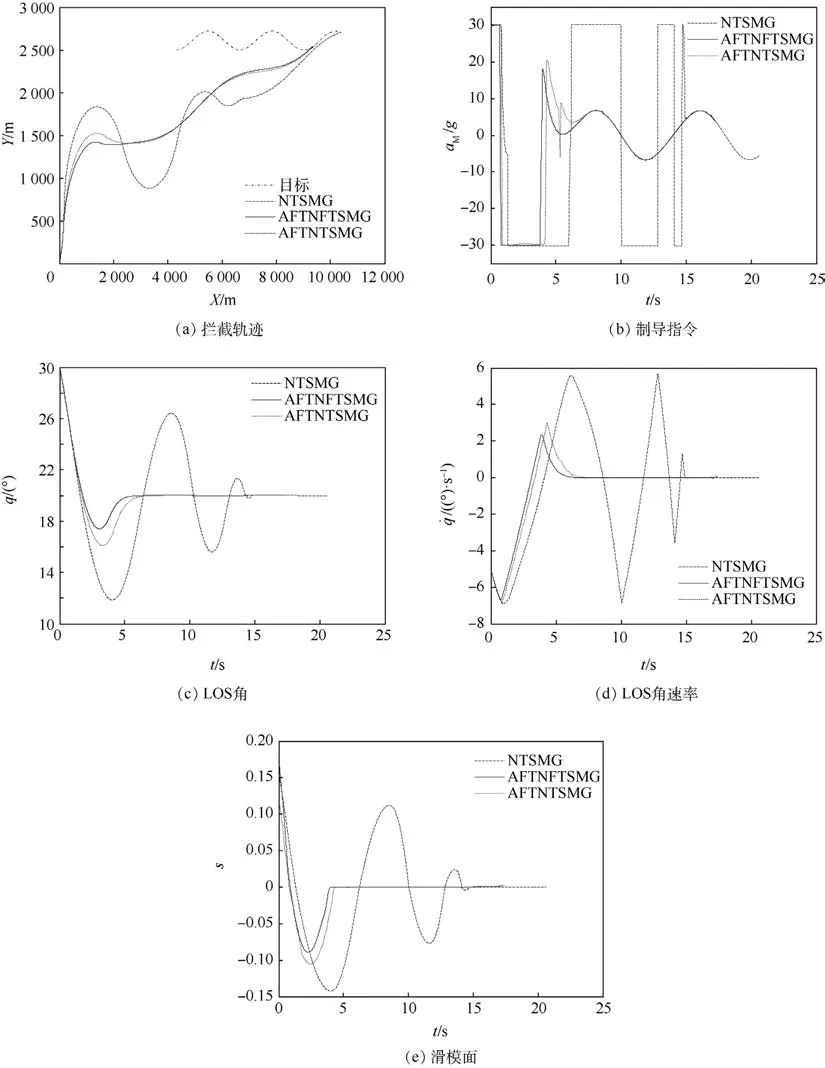
图6 不同制导律仿真对比Fig.6 Simulation comparison of different guidance laws

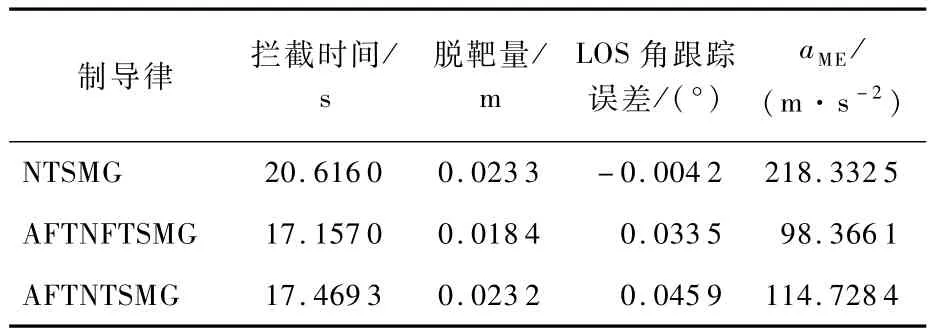
表2 不同制导律下拦截目标时的仿真结果Tab1e 2 Simu1ation resu1ts of intercepting target under different guidance 1aws

4 结 论

1）本文设计了一种新的带有攻击角度约束的终端滑模制导律，通过Lyapunov稳定性理论证明了导弹在满足终端角度约束的要求下能够成功拦截目标，并且制导系统的状态变量能够在固定时间T内收敛。

2）提出了一种固定时间收敛非奇异快速终端滑模控制方法，在保证滑模面不存在奇异问题的情况下，相较于现有的固定时间收敛控制，制导系统收敛速率更快。同时，对目标机动上界的自适应估计增强了制导系统的鲁棒性。

3）仿真结果表明，本文设计的制导律能够使导弹以不同的初始航迹角和不同的终端攻击角度拦截机动目标。通过与现有制导律对比，本文设计的制导律能够使导弹以更短时间和更高精度对目标实施打击，并且制导系统收敛速率更快，导弹消耗的能量更少。