双剪连接件及双耳连接耳片疲劳寿命估算的逐次累计求和算法

陈迪，李钰，张亦波，宋颖刚，熊峻江，*

（1.北京航空航天大学 交通科学与工程学院，北京100083； 2.中国商飞上海飞机设计研究院，上海200232；3.中国航发北京航空材料研究院，北京100095）

机械连接件（包括螺栓、铆钉和销钉连接件）具有易于拆卸、维修和替换的优点，广泛地应用于飞机结构，例如机身和机翼的蒙皮、翼肋和翼梁等[1-2]，然而，机械连接件的紧固孔周围存在应力集中和难以避免的加工缺陷，极易造成飞机结构件发生过早的疲劳失效，因此，机械连接件的疲劳和裂纹扩展性能受到广泛关注，并得到大量研究。研究表明，螺栓预紧力[1-4]、过盈配合[4-7]、冷扩孔[7-9]、钻孔工艺[10]和连接形式[11]等因素对机械连接件的疲劳和裂纹扩展性能产生重要影响。为预测机械连接件的疲劳寿命，前人先后提出了基于应力集中系数的名义应力方法[12-17]和考虑了局部塑性影响的局部应力-应变方法[18-19]，但是，此2种方法均无法考虑初始缺陷对于疲劳寿命的影响。事实上，机械连接件的初始缺陷（如材料夹杂和加工划痕等）往往难以避免，因此，前人提出了基于断裂力学和等效初始缺陷尺寸的损伤容限方法[20-24]。长期以来，疲劳方法和损伤容限方法互为补充，一直是结构寿命分析与设计的重要手段。

随着计算机技术和有限元计算的发展，人们越来越多地将疲劳理论、断裂力学、有限元分析和计算机相结合，发展复杂结构（包括连接件等）的疲劳损伤全过程的模拟技术（即虚拟疲劳试验技术）[25-28]，在得到足够的试验结果验证后，以期代替实物试验，提高结构设计与验证的效率，节省成本。为此，本文首先在双剪连接件及双耳连接耳片疲劳试验的基础上，通过扫描电子显微镜（SEM）分析，研究了其破坏模式和机理，并判读了疲劳裂纹形成与扩展寿命；然后，根据名义应力法和线弹性断裂力学法，发展了复杂连接件疲劳裂纹形成与扩展寿命估算的逐次累计求和算法；最后，运用本文提出的寿命估算算法估算了双剪连接件的疲劳裂纹形成寿命、双剪连接件和双耳连接耳片的疲劳裂纹扩展寿命，估算结果与断口判读结果吻合良好。研究结果对典型连接件结构的疲劳寿命分析与设计提供了有益参考。

1 连接件疲劳寿命估算算法

1.1 连接件疲劳裂纹形成寿命的算法

根据疲劳知识可知[29-30]，应力严重系数是制约复杂连接件疲劳寿命的关键因素，其表达式为

式中：L为应力严重系数；α为孔的表面状态系数；β为紧固件和连接板间的填充系数；σref为危险截面对应的名义应力；F为旁路载荷；ΔF为紧固件传递载荷；Kta为旁路应力引起的应力集中系数；Ktb为挤压应力引起的应力集中系数；W为板宽；t为板厚；d为紧固孔直径；φ为挤压应力分布系数。

由于疲劳强度总是随着应力严重系数的增大而降低，应力严重程度对复杂连接件疲劳强度的影响系数可写为[31]

式中：A1、A2和A3为材料常数。

考虑应力严重系数的影响，复杂连接件疲劳强度（或疲劳极限）变为

式中：S0为光滑试样的疲劳极限。

工程上，通常采用S-N曲线表征材料恒幅载荷下的疲劳性能，且三参数幂函数S-N曲线的使用最为广泛，复杂连接件的三参数幂函数S-N曲线表达式为

式中：Smax，R0为应力比R0下的最大名义应力；N为疲劳寿命；A和γ为材料常数，由疲劳试验数据拟合获得。

将式（3）代入式（4），得到指定应力比 R0下复杂连接件的三参数疲劳性能S-N-L曲面模型：

为描述任意应力比R下的疲劳性能，利用Goodman等寿命方程[29]，对式（5）进行修正，获得任意应力比R的疲劳性能S-N-L曲面模型：

式中：Sa为名义应力幅值；Sm为名义应力均值；σb为材料强度极限。

根据名义应力法和式（6），可估算谱载作用下复杂连接件疲劳寿命，即

式中：ni为载荷谱一周期内应力水平（Sai，Smi）对应的循环数；M为载荷谱一周期内的应力水平个数。

需要强调的是，利用ABAQUS等商用软件，在复杂连接件有限元建模过程中，已考虑了紧固孔填充、螺钉挤压、螺栓预紧力和摩擦等因素的影响，因此，在复杂连接件的应力集中系数Kt的计算结果基础上，仅需再考虑表面状态效应。

1.2 连接件疲劳裂纹扩展寿命的算法

根据线弹性断裂力学理论[32]可知，混合裂纹扩展的裂纹前缘的张开型（Ⅰ型）、滑开型（Ⅱ型）和撕开型（Ⅲ）应力强度因子为

式中：KⅠ、KⅡ和 KⅢ分别为Ⅰ、Ⅱ和Ⅲ型应力强度因子；u、v和w分别为裂纹前缘附近点局部直角坐标系下x、y和z方向的位移；r为裂纹前缘附近点局部极坐标系下极轴方向的坐标；G为材料的剪切模量；κ为与泊松比μ相关的系数，平面应力状态下，κ=（3-μ）／（1+μ），平面应变状态下，κ=3-4μ。

从式（8）可以看出，只要能够获取裂纹尖端附近的位移场，就可获取裂纹尖端的应力强度因子。基于最大能量释放率准则[33]，裂纹扩展角度θ可由式（9）计算：

式中：KC为材料的断裂韧度。

材料裂纹扩展速率性能常用四参数Forman模型表征：

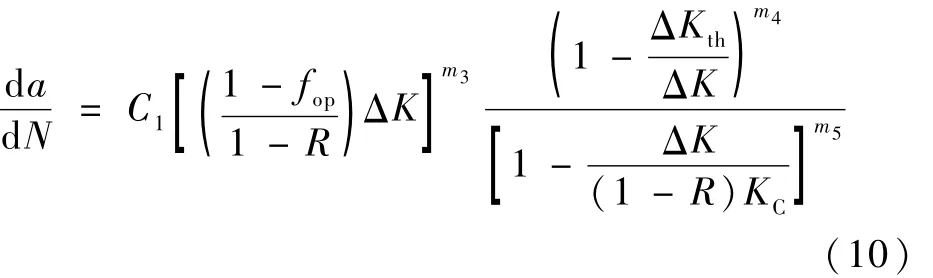
式中：

其中：

式中：C、m1～m5为材料参数；ΔK为应力强度因子变程；ΔKth为裂纹扩展门槛值；fop为疲劳裂纹张开函数；Smax为最大名义应力；α0为约束因子，对于平面应力状态，α0=1，对于平面应变状态，α0=3；σ0为流动应力；σs为材料的屈服极限。

对于混合扩展模式，需综合考虑 KⅠ、KⅡ和KⅢ对裂纹扩展速率的影响，引入等效应力强度因子[34]：

由式（10）和式（17），可得第 i个循环载荷作用后的裂纹长度ai为

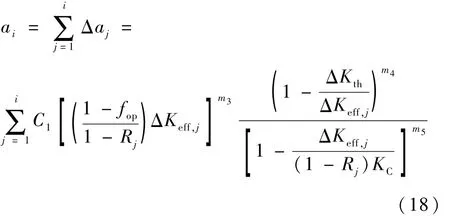
图1给出了三维裂纹扩展角度与长度关系示意图。利用有限元软件，在裂纹前缘上布置节点，施加疲劳循环载荷，各节点在其法平面内扩展。由式（8）、式（9）和式（18），分别计算裂尖各节点的应力强度因子、扩展角度 θ和长度 Δa，并拟合得到载荷循环作用后的当前裂纹前缘的位置和形状，重复上述过程，直至裂纹扩展至临界裂纹长度，此时的载荷循环次数即为连接件的裂纹扩展寿命。

图1 三维裂纹扩展角度与长度示意图Fig.1 Schematic of angle and length for 3D crack growth

2 疲劳试验

疲劳试验件共有2类：①双剪连接件，由盖板、芯板和螺栓构成；②双耳连接耳片，由耳片和销棒构成，2个耳片上均预制了电火花切口，试验中将销棒无衬套地插入耳片孔内，并通过销棒对耳片施加垂直于切口平面的疲劳载荷。2类连接件的形状和尺寸分别如图2所示，各部位的材料及力学性能如表1所示[35]，其中，E为材料弹性模量。

按照 ASTM E468—90试验方法[36]，在 MTS-880伺服液压疲劳试验机上进行疲劳试验，试验环境为大气室温，加载波形为正弦波，加载频率f=10 Hz，双剪连接件的加载方向沿试验件长度方向，双耳连接耳片沿图2（b）中外力P方向。2类连接件疲劳试验结果如表2所示。

通过试验发现，双剪连接件疲劳断口通过芯板螺栓孔（见图 3（a）），断口 SEM照片（见图3（b））表明，断面上共有5个裂纹：裂纹A～E，其中裂纹A～D萌生于芯板的搭接面，裂纹A与裂纹B位于螺栓孔同侧，沿板厚方向相向扩展，裂纹C与裂纹D位于螺栓孔的另一侧，同样沿板厚方向相向扩展，裂纹E萌生于孔壁与搭接面的交角处，沿板材厚度和宽度方向同时扩展。裂纹A～E的长度分别为 4、2.5、2.5、2.5和 1 mm，可见，裂纹 A面积最大，扩展最为充分，为主裂纹。主裂纹疲劳源不在螺栓孔边，这说明螺栓预紧力减轻了孔边的应力集中，使得主裂纹萌生位置偏离了螺栓孔，但在疲劳载荷的作用下，疲劳裂纹因扩展而不断靠近，甚至穿透螺栓孔边，直至断裂。

图2 双剪连接件和双耳连接耳片形状和尺寸Fig.2 Geometry and dimensions of double-lap joints and double-lug joints

表1 材料力学性能[35]Tab1e 1 Mechanica1properties of materia1s[35]

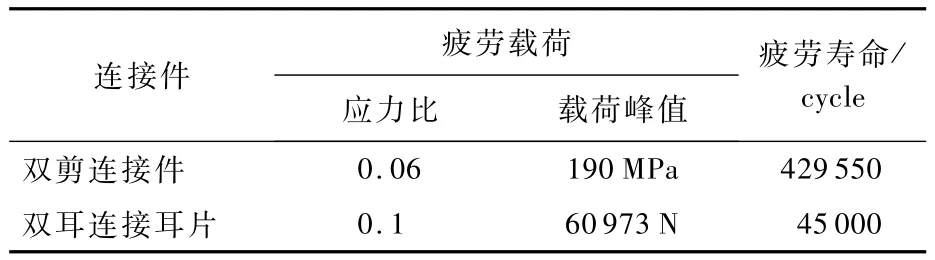
表2 疲劳试验结果Tab1e 2 Resu1ts of fatigue tests

双耳连接耳片的疲劳断口为通过切口A的剖面（见图 4（a）），断口 SEM照片（见图 4（b））表明，裂纹萌生于切口A的根部，并在切口所在平面，沿耳片宽度和厚度方向同时扩展，裂纹长度约为17.85 mm，断面平坦，疲劳扩展区约占整个断面面积的90%。

图3 双剪连接件的疲劳失效Fig.3 Fatigue failure of double-lap joint

图4 双耳连接耳片的疲劳失效Fig.4 Fatigue failure of double-lug joint

3 断口裂纹长度的SEM判读

图5 断口SEM照片Fig.5 SEM photographs of fracture

为了理解双剪连接件和双耳连接耳片的疲劳失效模式和机理，对2类连接件的断口进行SEM分析（如图5所示）。双剪连接件的疲劳源呈点源（见图5（a））；裂纹扩展区域发现细密的疲劳条带（见图5（b）），由于裂纹前缘存在较强的应力集中，部分裂纹表面被撕裂，形成沿条带分布的二次裂纹，二次裂纹可以释放裂纹前缘的应变能，从而降低主裂纹在扩展平面上的扩展速率；裂纹扩展后期，断口上出现等轴韧窝形貌（见图5（c）），说明此时双剪连接件发生了正应力导致的瞬断。双耳连接耳片的疲劳源位于切口根部，呈线源（见图5（d））；裂纹扩展区同样发现细密的疲劳条带（见图5（e）），由于裂纹扩展速率较快，材料发生相对滑移，疲劳条带旁边出现孔洞；裂纹扩展后期，断口上也出现等轴韧窝形貌（见图5（f）），与双剪连接件韧窝形貌相比，其韧窝大而浅，并在底部发现第二相颗粒，此时双耳连接耳片上的裂纹进入快速扩展阶段。

在疲劳载荷作用下，结构每承受一次应力循环，断口上就会留下一条疲劳条带，该疲劳条带是该次载荷循环作用时裂纹前缘的位置，疲劳条带数量与载荷循环次数相等[37]，因此，测量并统计断口上的疲劳条带数目，即可反推出裂纹的扩展寿命。

由于疲劳源附近往往无法清晰地观察到疲劳条带的分布情况，在进行断口定量反推时，以疲劳源为起点，沿着裂纹扩展方向进行观察，以稳态扩展区寻找到的第1条可识别的疲劳条带作为裂纹扩展的起点。断口上的疲劳条带数量繁多且分布密集，铝合金中部分元素会导致局部脆性增强，从而造成部分疲劳条带缺失，所以，断口很难呈现大面积规则的疲劳条带。为此，本文采用分段反推方法，即在稳态扩展区选取n条清晰的疲劳条带（标号1～n），将裂纹扩展过程分为n-1个阶段，其中将裂纹扩展起点作为第1条疲劳条带，将裂纹扩展终点作为第n条疲劳条带，值得注意的是，分段反推方法仅要求各阶段的起点和终点处的疲劳条带清晰即可。

为预测第k-1至第k条疲劳条带间的裂纹扩展寿命，在第k-1和第k条疲劳条带上分别选取3个位置（如图6（b）中①②③），利用高倍扫描电子显微镜分别测量3个位置处与前后疲劳条带的间距 S（k1）和 S（k2），取3个位置处的 S（k1）和的平均值作为该疲劳条带处的间距 Sk，并将（Sk+Sk-1）／2作为第 k-1至第 k条疲劳条带阶段的平均扩展速率，则第k-1至第k条疲劳条带阶段的裂纹扩展寿命为

式中：ak-1和ak分别为第k-1条和第k条疲劳条带对应的裂纹长度。

图6 断口判读方法Fig.6 Fracture interpretation method

裂纹长度达到 ak时所经历的载荷循环次数为

2类连接件的断口判读结果如表3、表4和图7所示。从表3可以看出，双剪连接件的裂纹扩展寿命判读值为13 760 cycles，由总疲劳寿命可反推出裂纹形成寿命判读值为415 790 cycles。从表4可以看出，双耳连接耳片的裂纹扩展寿命判读值为33 283 cycles，则裂纹形成寿命判读值为11717 cycles。从图7可以看出，双剪连接件的裂纹始终以较稳定的速率进行扩展，而双耳连接耳片的裂纹在扩展中前期速率较为稳定，但在扩展后期，裂纹扩展速率迅速增加，进入不稳定的快速扩展阶段。

表3 双剪连接件的裂纹扩展寿命Tab1e 3 Cr ack growth 1ife of doub1e-1ap joints

表4 双耳连接耳片的裂纹扩展寿命Tab1e 4 Cr ack growth 1ife of doub1e-1ug joints

图7 裂纹长度与裂纹扩展寿命Fig.7 Crack length versus crack growth life

4 连接件寿命估算

4.1 连接件裂纹形成寿命

利用ABAQUS有限元软件，建立双剪连接件的有限元模型（如图8（a）所示），采用线性六面体C3D8R单元模拟双剪连接件，生成了63 939个单元。在2个盖板的夹持端施加固支约束，在芯板的夹持端施加纵向均布拉伸载荷，在2个螺栓的上下表面对称地施加0.1 mm的轴向压缩位移以模拟螺栓预紧力对板的压缩作用。

双剪连接件各部件的材料性能按表1进行设置，各部件间的接触属性设置为法向“硬接触”和切向库伦摩擦接触，摩擦系数设置为0.5。计算得到双剪连接件应力分布如图8（b）所示，计算得到应力集中系数Kt=1.49。

图8 双剪连接件有限元模型Fig.8 Finite element model for double-lap joints

根据抗疲劳设计手册[30]，选取表面状态系数α=1.2，计算得到应力严重系数 L=1.79。

根据2324-T39的疲劳性能数据[38]，获得疲劳性能S-N-L曲面：

将双剪连接件的应力严重系数及疲劳载荷循环（见表2）代入式（21），预测出双剪连接件的疲劳裂纹形成寿命为371 270 cycles，与断口判读结果（415 790 cycles）的相对偏差为10.7%，具有可接受精度。

4.2 连接件裂纹扩展寿命

图9 双剪连接件裂纹扩展模拟Fig.9 Crack growth simulation of double-lap joints

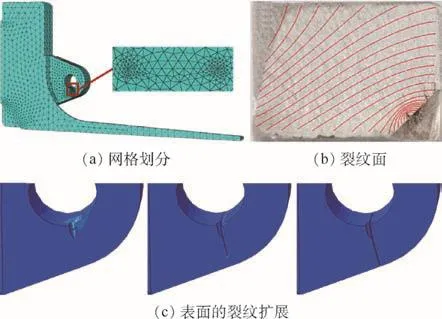
图10 双耳连接耳片裂纹扩展模拟Fig.10 Crack growth simulation of double-lug joints

利用ABAQUS有限元软件，建立含初始裂纹的双剪连接件和双耳连接耳片的有限元模型（见图9和图10），根据断口疲劳裂纹判读结果，双剪连接件断面上存在5条裂纹，其中A裂纹是主裂纹，B、C、D和 E裂纹虽然形成，但未同时扩展或扩展非常缓慢，因此，B、C、D和 E裂纹对结构刚度和应力分配无明显影响，对主裂纹扩展行为的影响也很小，可忽略不计。在双剪连接件和双耳连接耳片上插入初始裂纹长度分别为0.05 mm和0.01 mm的半圆形裂纹，裂纹尖端均选用1／4节点楔形奇异单元来划分网格（见图9（a）和图10（a））。采用线性六面体C3D8R单元模拟双剪连接件，生成64 847个单元，边界条件及接触设置与前面相同。采用线性六面体C3D8R单元和二次四面体C3D10单元分别模拟双耳连接的耳环和底座，分别生成10 724和6 055个单元；双耳连接耳片的上、下和侧表面均施加固支约束，销棒加载端面上施加均布拉伸载荷，拉伸载荷方向与图2（b）中P方向一致，部件间的接触属性设置为法向“硬接触”和切向库伦摩擦接触，摩擦系数设置为0.3。

首先，对有限元模型逐个施加疲劳载荷循环，根据式（8）和式（17），计算裂纹前缘应力强度因子；然后，根据连接件材料裂纹扩展速率的四参数Forman模型[37]（式（22）和式（23）），计算裂纹扩展长度；最后，利用式（9），计算裂纹扩展角度，从而获取下一个载荷循环对应的裂纹前缘形状，不断重复上述过程直至裂纹长度达到临界裂纹长度，输出裂纹扩展过程模拟结果如图7、图9（b）、图 9（c）、图 10（b）、图 10（c）、表 3和表 4所示。

从表3、表4和图7可以看出，双剪连接件和双耳连接耳片的疲劳裂纹扩展寿命估算值分别为10 641 cycles和26 242 cycles，预测值与断口判读值的最大相对误差分别为46.1%和21.2%，具备可接受精度。从图 9（b）、图 9（c）、图 10（b）和图10（c）可以看出，本文算法能有效模拟2类连接件的裂纹扩展过程，模拟的裂纹前缘形状与断面裂纹形貌吻合良好。

5 结 论

1）基于应力严重系数法和线弹性断裂力学法，建立了复杂连接件疲劳性能S-N-L曲面，发展了估算复杂连接件疲劳裂纹形成与扩展寿命的逐次累计求和算法。

2）利用SEM分析技术，研究了双剪连接件和双耳连接耳片的疲劳失效机理，测量并统计了断口上的疲劳条带数目，反推出2类连接件的疲劳裂纹形成及扩展寿命。

3）利用逐次累计求和算法，估算了双剪连接件的疲劳裂纹形成寿命、双剪连接件和双耳连接耳片的裂纹扩展寿命，估算结果与断口判读结果吻合良好。