数形结合思想在初中数学解题中的应用

筅山东省淄博市淄川区磁村中学 李广潇

图1

一、利用数形结合思想比较实数的大小

我们知道，比较实数大小的方法比较多，如平方法、倒数法、作差比较法、作商比较法、估算法等.然而，有些比较实数大小问题使用这些方法解决比较麻烦，不太奏效，如果借助数形结合思想来比较实数大小，往往显得非常简捷.

例1证明：在这三个数中，任意两个数之和大于第三个数.

图2

证明：如图2，构造一个边长为3的正方形ABCD.分别在边AD、CD上取点E、F，使AE=1，DF=1，则DE=2，CF=2.在Rt△DEF中，由勾股定理，得EF=；在Rt△ABE中，由勾股定理，得BE=；在Rt△BCF中，由勾股定理，得BF=.在△BEF中，由三角形的三边关系定理，可得在、这三个数中，任意两个数之和大于第三个数.

思考：如果一个三角形的三边长分别为，你会求这个三角形的面积吗？怎样求解比较简捷？

二、利用数形结合思想求相遇的次数

在数学上有一个著名的“柳卡问题”，它是利用数形结合思想解决数学问题的典范.一些中考题正是以“柳卡问题”为背景衍生而成的.解答此类中考题也要注意作出一次函数的图像，利用数形结合思想求两者相遇的次数.

例2一巡逻艇和一货轮同时从A港口前往相距100千米的B港口，巡逻艇和货轮的速度分别为100千米/时和20千米/时，巡逻艇不停地往返于A、B两港口巡逻（巡逻艇调头的时间忽略不计）.求货轮从A港口出发后直到B港口与巡逻艇一共相遇了几次.

分析：首先应该明白，无论是巡逻艇同向从后面追赶上货轮，还是巡逻艇相向从前面与货轮碰头，都算相遇.本题若按常规方法，需要考虑巡逻艇与货轮行驶的细节，即第一次货轮与从B港口返回的巡逻艇迎面相遇；第二次货轮与从A港口再次出发追赶来的巡逻艇相遇……由于货轮与巡逻艇迎面相遇的路程在改变，巡逻艇从后面追赶货轮的追及路程也在改变，因而比较麻烦.如果利用数形结合，只需作出货轮从A港口出发直至行驶到B港口，以及巡逻艇从A港口出发在两个港口往返的行驶时间与路程之间的函数关系图，交点的个数即为货轮与巡逻艇相遇的次数.

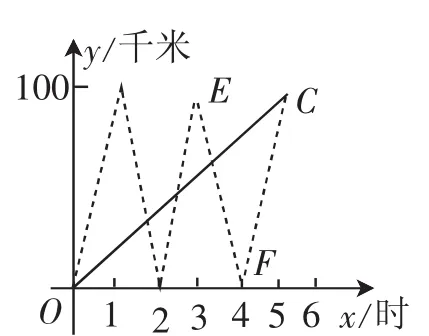
图3

解：如图3所示，先作出货轮从A港口出发直至行驶到B港口行驶时间与路程之间的函数关系图（用图中实线表示），在同一直角坐标系中再作出巡逻艇从A港口出发在两个港口往返的行驶时间与路程之间的函数关系图（用图中虚线表示）.从图中可以看出，实线与虚线部分一共有4个交点，所以货轮从A港口出发后直到B港口与巡逻艇一共相遇了4次.

点评：从图3可以看出，我们不仅可以求出货轮与巡逻艇相遇的次数，而且可以求出每次相遇的时间.

三、利用数形结合思想比较字母的大小

比较字母大小的通常方法是从数轴或函数图像上面获取字母间大小关系信息，利用不等式的性质比较大小，有时很麻烦.有些比较字母大小问题如果能够根据函数与方程之间的关系，利用数形结合，可以获得简解.

例3已知x1、x2（x1＜x2）是方程（x-a）（x-b）=1（a＜b）的两个根，则实数x1、x2、a、b的大小关系是＿＿＿＿＿＿.

分析：表面上看，这是一个一元二次方程有关的问题，可先求出方程（x-a）（x-b）=1（a＜b）的两个根，然后比较大小.利用一元二次方程的求根公式及x1＜x2，得x1=a+b-，x2=.x1-a=a+b--a=b-a-.由a＜b，得b-a＞0.显然b-a＜则＜0.即x1-a＜0.则x1＜a.x2-b=-b==由a＜b， 得b-a＞0. 显 然b-a＜则＞0.即x2-b＞0.则b＜x2.则x1＜a＜b＜x2.这种解法比较麻烦，主要是因为从一元二次方程的角度求解.联想到二次函数的图像与一元二次方程的关系，我们可以借助抛物线，数形结合进行巧解.

解：实数a、b是方程（xa）（x-b）=0的两个根，它可以看作抛物线y=（x-a）（xb）与x轴的两个交点的横坐标.方程（x-a）（x-b）=1的两个根可看作抛物线y=（x-a）（x-b）-1与x轴的两个交点的横坐标.抛物线y=（x-a）（x-b）-1可由抛物线y=（x-a）（x-b） 向下平移1个单位得到，如图4所示.观察图形不难发现，实数x1、x2、a、b的大小关系为x1＜a＜b＜x2.

点评：显然这样求解十分简捷.初看此题，有一种望而生畏、不知所措之感.注意到二次函数y=（x-a）（x-b）-1与y=（x-a）（x-b）的图像之间的关系，联想到二次函数与一元二次方程的关系，问题迎刃而解.

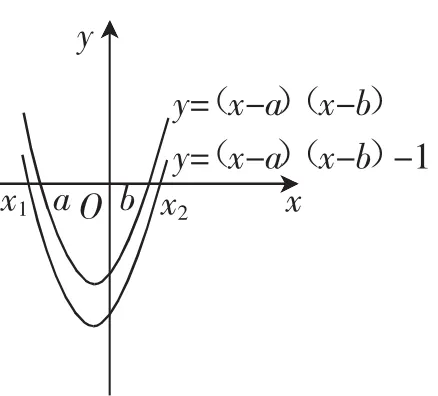
图4

初中数学中利用数形结合的例子是多方面的，例如，利用数轴表示正实数、负实数和0；利用数轴确定不等式组的解集时，先在数轴上分别表示出每一个不等式的解集，然后找出公共部分，这个公共部分就是不等式组的解集；在同一平面直角坐标系中作出两个一次函数的图像，通过观察图像的交点坐标确定对应二元一次方程组的近似解；在行程问题中，经常通过画图理解题意、分析问题；利用拼图的方法证明勾股定理；通过图形面积之间的关系理解平方差公式和完全平方公式的几何意义等.希望大家能够真正理解数形结合思想，并灵活应用数形结合思想解决数学问题.