在“挑战难题”的学程中生成新知——以“三角形中位线性质”教学为例

筅江苏省海安市海陵中学 魏爱凤

最近一次教研活动中，笔者有机会执教“三角形中位线性质”，备课过程中几易其稿，从最初根据教材按部就班地“照本宣科”到“习题题组呈现的变式教学”设计，再到最后基于“问题驱动”式的教学设计，笔者对这节课教学内容的理解也逐渐加深.从课堂实践来看，也取得了较理想的教学效果.本文先整理该课最后定稿的教学设计，并给出教学立意的阐释，供研讨.

一、三角形的中位线新授课教学设计

1.从数学现实出发，激发学生挑战兴趣

课前，在黑板上先画出几个三角形，开课后依次在这些三角形中画出三条角平分线、三条边的垂直平分线（如图1和图2），学生都能肯定它们交于一点，并且此前都进行过证明.

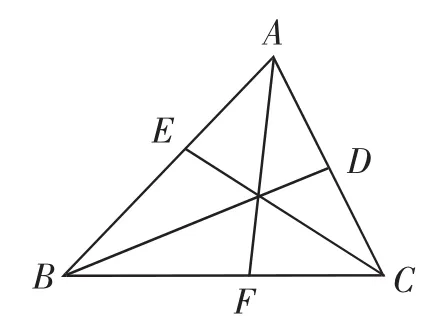
图1

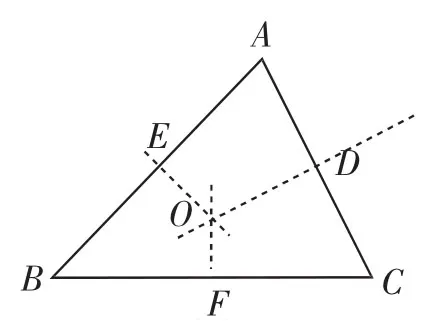
图2

在图3中，要求学生画出三边的中线，大家会发现三边的中线竟然也能交于一点！如何证明呢？学生挑战，2分钟后，教师可告知大家，这个太难了，需要用到平行四边形的知识，所以之前我们在学习三角形或全等时都没有涉及这个奇异的性质，这节课我们来一起攻克这个遗留难题.

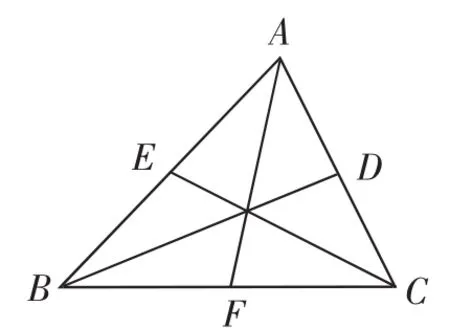
图3

2.发现并证明三角形中位线性质定理

问题1：让我们从平行四边形出发，如图4，平行四边形ABCD中，对角线AC、BD交于点O，延长AB到E，使BE=AB，连接CE.图中又出现了一个平行四边形，请大家找出来，并证明.

教学组织：学生很快会证出四边形BECD为平行四边形，安排另一个学生复述一下证明思路，不必给出书面表达，因为这不是本课的教学重点，以便节约课堂时间.接下来教师将图4中有些线段擦去，得到图5，提出问题：

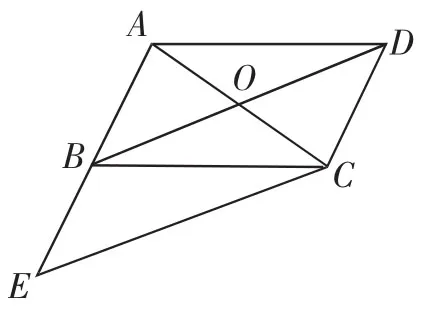
图4

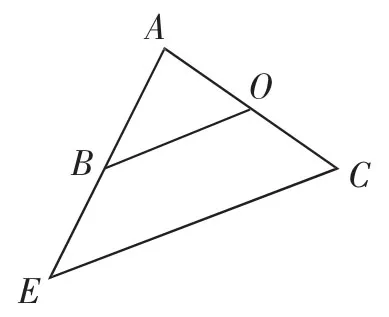
图5

问题2：在△AEC中，B、O分别是边AE、AC的中点，探究线段BO与CE的数量关系、位置关系.

教学组织：安排学生独立思考，待学生有思路后教师巡查、交流，然后让学生分组讨论证明思路，最后安排两个小组派代表上台讲解辅助线的构造与证明思路.多数学生应该能想到转化为图4进行证明.

引导归纳：如图6，△ABC中，D、E分别是边AB、AC的中点，连接DE，定义线段DE为△ABC的中位线.请大家想想，一个三角形的中位线有几条，它们与三角形的第三边有怎样的关系？你会证明吗？

教学组织：学生有了前面图5的证明经验，很快就可归纳出三角形的中位线性质定理，教师进行板书，并安排学生写出该定理的符号表示形式.

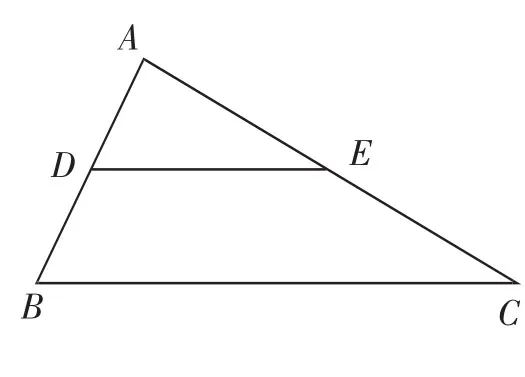
图6

3.迎难而上，挑战难题

过渡：让我们开始挑战“三角形三边中线交于一点”这个难点.与以前证明三角形三条角平分线交于一点类似，如图7，也先设两条中线交于一点M，我们试图证明点M也在第三条中线上.证明思路比较独特，考虑到今天课堂学习时间有限，老师帮助大家提供一种思路导引，一起来看问题3.问题3：如图7，BD、CE是三B F C角形ABC的两条中线，它们交于点M.小晶度量后发现，点M恰是BD、CE一个三等分点.她换了一个图之后，如图8，点M′竟然也是中线BD、AF的一个三等分点.你能发现其中的道理吗？

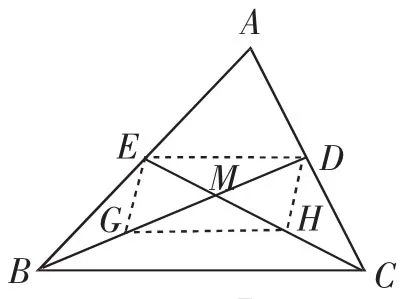
图7

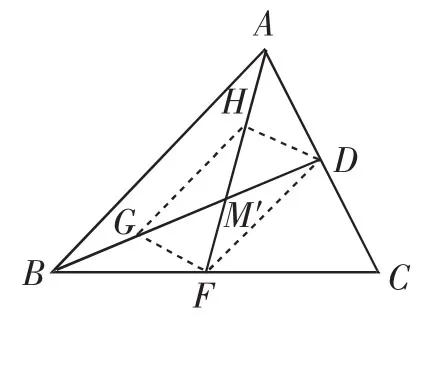
图8

教学组织：提示学生取BM、CM的中点G、H，顺次连接点D、E、G、H，利用三角形中位线性质证明四边形DEGH是平行四边形，从而可以贯通思路.在图8中，可以安排学生在小组内交流，再在大组内讲解思路，通过学生变换不同图形（图7或图8）连续两到三次的重复讲解，让更多学生跟上证明思路，加深对任意两条中线的交点都是中线的一个三等分点的认识，从而确认点M是三条中线的交点，也攻克了开课阶段提出的疑难问题.

归纳性质：三角形三条中线交于一点，并且这点恰是中线的一个三等分点.（可以向学生介绍这个点称为重心，这个性质就是著名的“重心定理”）

4.课堂小结，反馈练习

小结问题1：本课内容主要学习三角形的中位线、中线相关内容，但安排在平行四边形这一章中，你觉得教材编写专家为什么这样安排？

小结问题2：通过本课的学习，你觉得三角形的中线与中位线有什么区别？

小结问题3：关于三角形的中位线和中线的区别，你们说得很好，它们有时也会有“关系”.比如，三角形一条中位线与第三边上的中线就能互相平分.你们能理解吗？小组内交流一下如何证明.

反馈练习：如图9，△ABC中，中线BD、CE交于G点，连接DE.

（1）若BC=5cm，求中位线DE的长.

（2）若CG=10cm时则GE的长为多少？

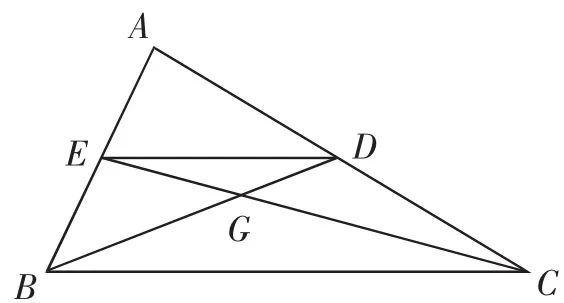
图9

（3）连接AG并延长交BC于点F，交DE于点M.

①小海认为AF一定是△ABC的中线.你觉得小海正确吗？（直接回答“正确”或“错误”）

②若AF=9cm，求GF的长为多少.

设计意图：全课没有安排例题，只在小结之后安排这个题组训练本课所学习的内容（涵盖三角形中位线性质、重心性质）.

二、教学立意的进一步阐释

1.深刻理解教学内容，精选数学现实驱动新课

三角形中位线没有安排在三角形一章学习的根本原因是：说清或证明它的性质时，结合平行四边形的性质与判定会更加便捷.将这个疑惑作为一个问题情境激发学生的学习兴趣与挑战欲望，就是一个较为恰当的“数学现实”，并将其作为“问题”驱动新课教学.这类数学现实的选择需要教师深刻理解教学内容，结合本课教学目标进行优选，而不是“照本宣科”，这也是从“教教材”走向“用教材教”的具体实践.

2.深刻理解学情、教情，开展“有指导的”新知教学

在教学内容确定之后，还需要结合学情与班情，想清辨明学生对待学内容或相关习题的接受程度，研判学生可能出现的障碍或困惑之处，在此基础上预设各个教学环节及铺垫式问题.比如，上文中对于“疑难问题”（求证三角形三边中线交于一点）在没有学习过的情况下，在这节课有限的教学时间内是难以快速突破的，所以就引出先研究三角形中位线的性质，进而帮助学生复习、类比三角形三条角平分线交于一点的证明思路，然后启发学生证明三角形两条中线交点的性质，这些都是课前铺垫、预设的，学生在这些“有指导的”教学点拨之后才能顺利解决，也能保证在课堂教学时间内完成教学任务.

3.精心预设小结问题，跟进习题训练反馈学情

本课另一个精心设计之处是几个“小结问题”，我们没有用一些“空而泛”的小结问题，如“这节课学到了什么？这节课你有什么收获”之类的问题，因为这些问题对于引导学生小结这节课所学不够精准，对本课教学重点、疑难点的辨析也不充分，所以我们让学生猜想教材编写者的编写意图，也让学生辨析中线与中位线的区别和联系，并在此基础上设计了一组问题串对本课所学的内容进行巩固训练，即时反馈学情.

三、写在后面

这次教研活动的教学设计与磨课经历让笔者知道教学即研究，教研无止境，专业精进永远在路上.面对三角形中位线性质，一年又一年重复教学过很多次，却仍然有值得深入思考的教研话题，这也启示我们，面对经典课题的教学，仍然要基于“三个理解”，精心备课，常教常新.想来，这也是“诲人不倦”的职业追求吧.

致谢：本课教学设计、试教打磨的全过程都得到海安市教师发展中心初中数学教研员刘东升老师的精心指导，谨致谢意！