应用VMD与Teager能量算子的结构模态系统辨识*

靳 行， 林建辉

(西南交通大学牵引动力国家重点实验室 成都，610031)

引 言

对于整体结构如齿轮箱、整备后的车辆等进行模态测试时，由于施加人工激励较为困难，因此通常直接利用环境激励下的输出信号识别模态参数。与传统的输入、输出的模态实验分析相比，直接利用输出信号识别模态参数具有测量简单、对近频与重频敏感、更接近真实动力特性等优点[1]。

环境激励下的模态参数研究除了常用的频域法与时域法，时频法也是近些年被国内外广泛关注的方法。例如Bao等[2]开发了一种自适应的时频方法来识别电缆的张力变化。Spiridonakos等[3]在实验室建立了桥梁-车辆系统时变频率的时变自回归移动平均模型。经验模态分解[4](empirical mode decomposition，简称EMD)通过将信号分解成多个单一频率的固有模式函数(intrinsic mode functions，简称IMF)，然后通过希尔伯特变换提取瞬时频率。陈双喜等[5]应用该方法有效地提取车辆-轨道垂向耦合系统动态特性。李康强等[6]应用EMD与能量算子有效提取行星齿轮箱各阶次的模态参数。然而在一些情况下，使用EMD方法提取的IMF由于模态混叠导致一系列频率，即IMF非单一频率。由于边界效应，导致IMF本身可能是虚假的伪分量。

为了克服EMD的种种限制与缺陷，变分模态分解(variational mode decomposition，简称VMD)应运而生[7]。 VMD方法继承了EMD的迭代思想，通过寻找中心频率，将信号进分解成不同尺度的细节信号。已经有研究表明，VMD在机械振动信号分析[8]、故障诊断[9-10]、电网预测[11]和地震信号分析[12]等领域的性能优于EMD方法。尽管应用VMD在许多方面表现出比EMD 的性能更加优异，但VMD也存在一些缺点，如层数参量K与罚参量α需要提前给定，其取值大小对计算结果影响尚缺乏理论依据[8]。

在此基础上，笔者提出基于VMD与TEO对输出信号的结构模态识别方法，并针对VMD参数选择这一缺陷，提出了通过调整层数参量K寻找稳定极点的作法，实现模态参数准确识别。首先，使用VMD算法对测量结构输出的加速度信号进行分解；其次，应用TEO算法得到瞬时频率与瞬时幅值来拟合固有频率与阻尼比；最后，将层数参量K作为一种最优解参考，通过观察不同VMD层数参量K时固有频率与阻尼比组成的极点，判断真实的模态参数。笔者分析了在冲击力作用下结构的数值模型，对比现有的方法以验证所提方法识别模态参数的准确性和有效性。实验研究了动车组齿轮箱的锤击法与环境激励的振动数据，结果表明，所提方法在识别结构模态数据方面是有效而准确的。

1 基本理论

1.1 结构模态系统

具有n阶自由度(degrees of freedom，简称DOF)的结构的运动方程可以写成

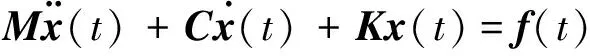
(1)

每阶模态固有频率都是一个窄带信号，由模态叠加原理可知，每个自由度均可通过 对n阶模态固有频率进行叠加，得到加速度响应

(2)

其中：Φi为第i阶模态振型；qi(t)为第i阶模态对应的响应函数。

当在第z个DOF上施加冲击力，并将式(2)带入式(1)中解耦，可以得到第i个广义模态坐标上i的加速度响应

(3)

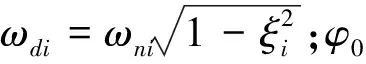
因此第p个自由度上的加速度响应可以写成

(4)

将式(4)写成调幅调制信号的形式

(5)

1.2 变分模态分解

VMD的方法原理与EMD方法十分相似，但是它放弃了EMD方法中循环筛选极值进行滤波的方法，而是将信号分解引入变分模型中来解决滤波问题。为了找到最优解，通过寻求约束变分模型，从而实现信号分解。在VMD分解的过程中，每个BIMF分量的中心频率及其带宽不断地交替迭代，自适应地分解为合适的信号频带，得到K个预设尺度下的BIMF 分量。变分约束问题为

(6)

其中：uk为模态函数集；ωk为每个模态函数集的中心频率；δ(t)为脉冲单位函数。

为了解决上述约束最优化问题，VMD 算法在实施过程中综合利用了二次惩罚项和拉格朗日乘子法的优势，引入了增广拉格朗日函数ζ，如式(7)所示

ζ({uk},{ωk},λ)=

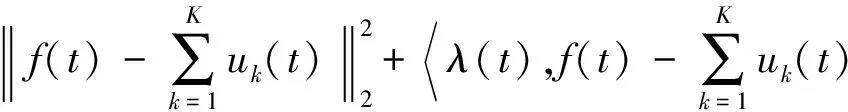
(7)

其中：α为罚参量；λ(t)为拉格朗日乘子。

解决式(7)中最小化问题的方法是：用交替方向乘子法进行一系列的迭代优化找到的极小值点。

VMD算法的分解详细过程可参考文献[7]。与EMD方法相似, 原始信号x(t)被分解为K个稳定的BIMF分量uk(t)及一个能量较低的残差信号ε(t)

(8)

VMD通过在变分问题框架中迭代搜索变分模型最优解来实现信号的分解，其本质是维纳滤波，具有很好的噪声鲁棒性，并且解决了EMD 算法存在的模态混叠、伪分量以及易受噪声干扰等缺点，保留了EMD算法可以有效抑制ln[Ak(t)]交叉项的优点。

1.3 Teager 能量算子

Teager能量算子是一个非线性算子，为了减少离散TEO算法的误差，笔者对TEO算子的求解进行了改进。采用改进后的TEO算法能准确地解调出原信号的瞬时频率TEO[13]，信号u(t)的能量算子Ψ[·]运算定义为

(9)

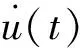
对该无衰减自由振荡的线性振子，其振动位移为x(t)=Acos(ωt+θ)。其中：A为振幅；ω为角频率；θ为初相。

对上式求1阶微分

(10)

改进的TEO算法是通过对Ψ[·]进行低通滤波，数字滤波器采用切比雪夫Ⅰ型，其单位脉冲响应为δ(n)，则有

Ψd[·]=δ(n)*Ψ[·]

(11)

用Ψd[·]替代Ψ[·]，便可得到改进的离散时间能量分离算法，即改进的离散TEO算法。由此得到瞬时包络A(t)和瞬时角频率ω(t)

(12)

1.4 模态固有频率与阻尼比的识别

对于小阻尼系统，可以根据模态响应的衰减幅值来计算阻尼比与固有频率[14]，由于模态响应与时间t之间存在以下关系

(13)

为了估计得到固有频率与阻尼比，使用最小二乘法进行线性拟合，可以得到固有频率ωn,k与阻尼比ξk。

2 分析步骤与方法

分析步骤与方法如下：

1) 为了减少计算量，避免弱衰减和零衰减部分对结果的影响，对原始信号截取明显衰减的部分进行VMD 分解，得到多个BIMF 分量；

2) 预设最大分解层数Kmax，将VMD层数参量设为K=1,2,…,Kmax，依次对n个测点的时域信号进行VMD分解，得到n∑Kmax个BIMF分量；

3) 设定低通频率，应用改进TEO算法得到瞬时幅值与瞬时频率，根据式(13)拟合得到不同层数参量K下每一个BIMF固有频率与阻尼比；

4) 根据层数参量K重新排列固有频率与阻尼比，在稳态图中观察极点列，选择不随层数参量K变化的稳定极点作为最终识别结果。

其中稳态图包含3种极点:

1) 首次出现的极点为原始极点;

2) 分解层数增加，原始极点的固有频率变化小于阈值的极点为频率极点；

3) 分解层数增加，原始极点或频率极点的频率变化与阻尼比变化均小于阈值的极点为稳态极点。

在稳态图中选择表现结构物理特性的极点，从一列极点的最低分解层数中找到稳定极点，与下一层极点比较，如果阻尼比较稳定，则选择该极点的固有频率与阻尼比作为最终识别结果。

3 仿真信号分析

3.1 仿真信号

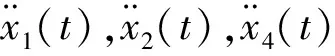
图1 五自由度模型Fig.1 The 5-dof numerical model

质量矩阵为

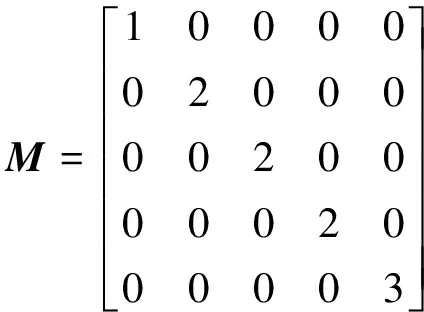
(14)

刚度矩阵为

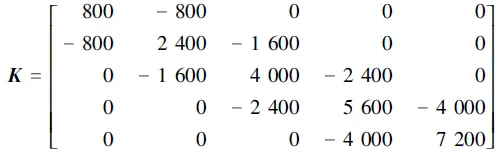
(15)

仿真中使用Rayleigh阻尼模型，阻尼为C=0.5M+0.000 4K，Newmark算法用于获得系统加速度曲线。采样频率为128Hz，冲击力施加在第1个自由度

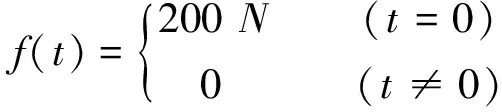
(16)

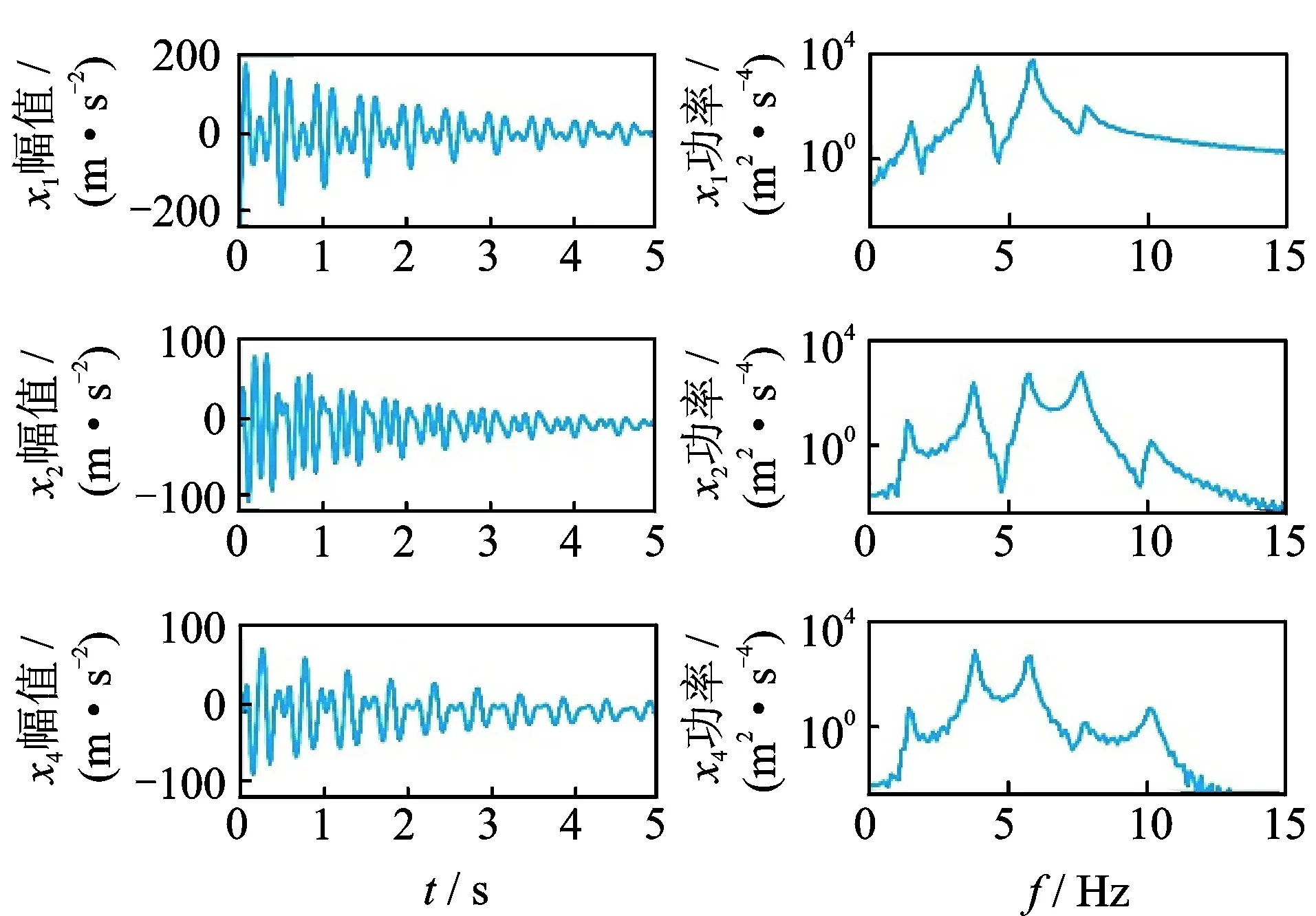
图2 系统的时域自由振动响应和相应的功率谱密度Fig.2 Time-domain free-vibration responses of the system and the corresponding power spectral density

3.2 同类方法比较

首先对振动响应进行VMD分解，最大分解层数Kmax=10 ，罚参量设为α=1 024，统计不同层数参量下模态识别结果。

为了突出本研究方法的创新性，采用两种同类方法进行对比。图3所示为采用文献[15]所述的Hilbert方法得到的稳态结果，图4所示为采用文献[16]所述的中心频率方法得到稳态结果。图5为本研究提出的TEO方法稳态结果。仿真信号中，频率变化阈值为1%，阻尼比变化阈值为5%。

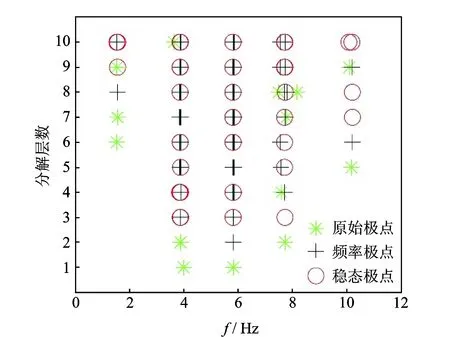
图3 Hilbert模态参数极点稳态图Fig.3 Modal parameter identification for Hilbert of stabilization diagra

如图4～6所示，稳态图中均存在5列明显的极点列。表1是根据稳态图中选择得到的固有频率。3种方法识别的固有频率与理论值接近。

表2对比了识别结果与理论值的误差，可以看出，笔者所提的TEO法识别的结果平均误差要小于前2种方法，固有频率识别的平均误差降了0.14%。

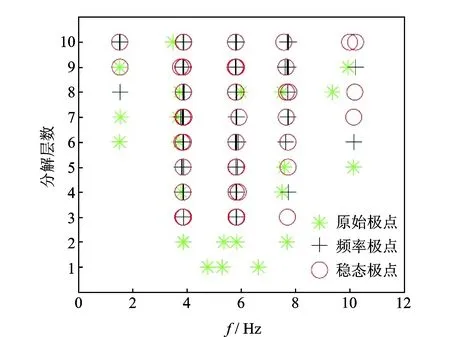
图4 中心频率模态参数极点稳态图Fig.4 Modal parameter identification for center frequency of stabilization diagra

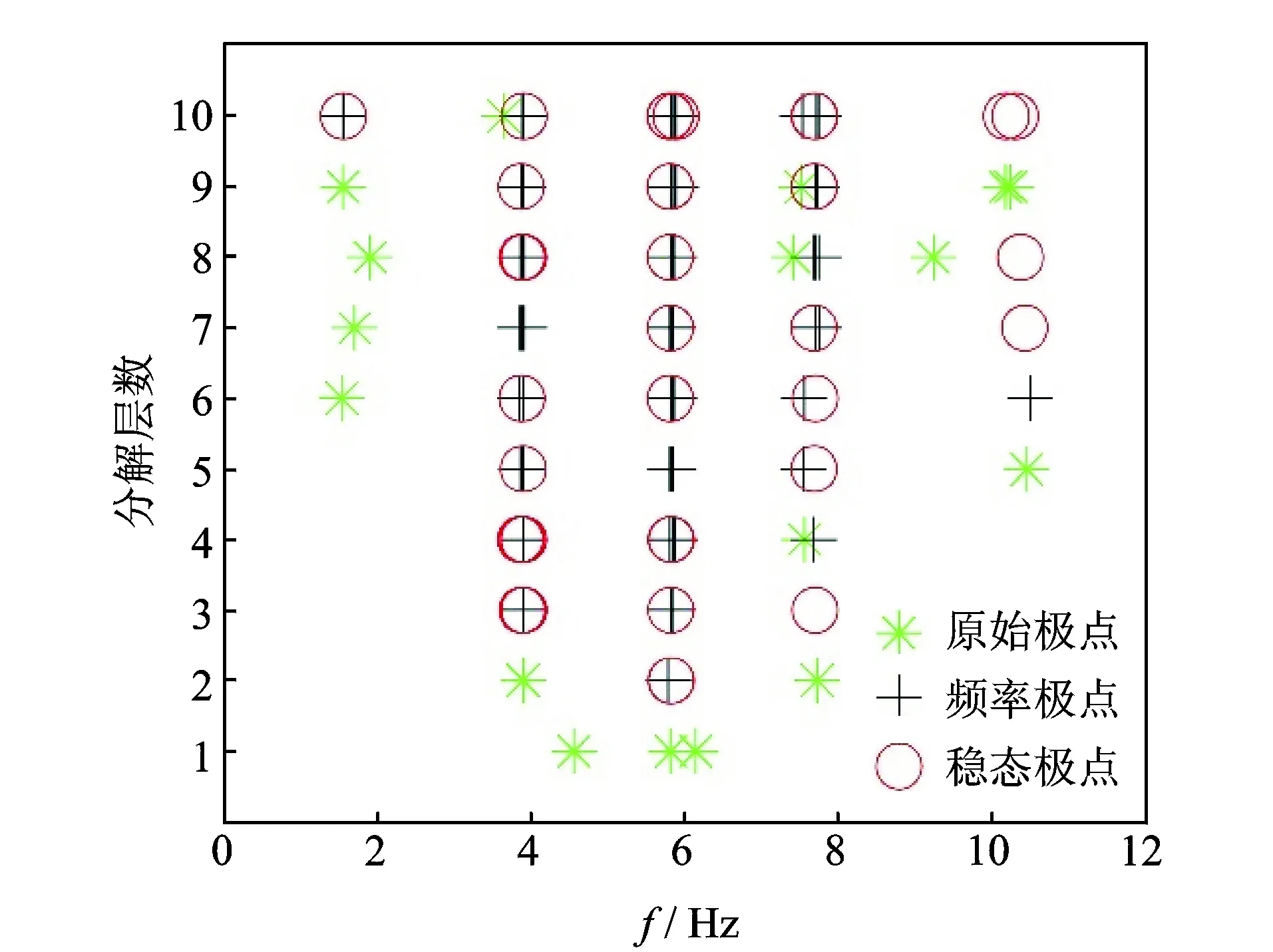
图5 TEO算法模态参数极点稳态图Fig.5 Modal parameter identification for TEO of stabilization diagra

表3为3种方法识别的阻尼比结果，结果与理论值存在一定偏差，如表4所示，笔者所提方法平均误差小于其他两种方法。

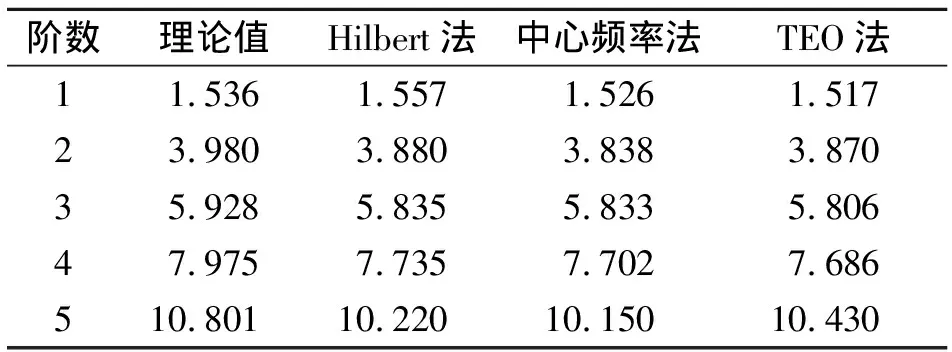
表1 仿真信号固有频率

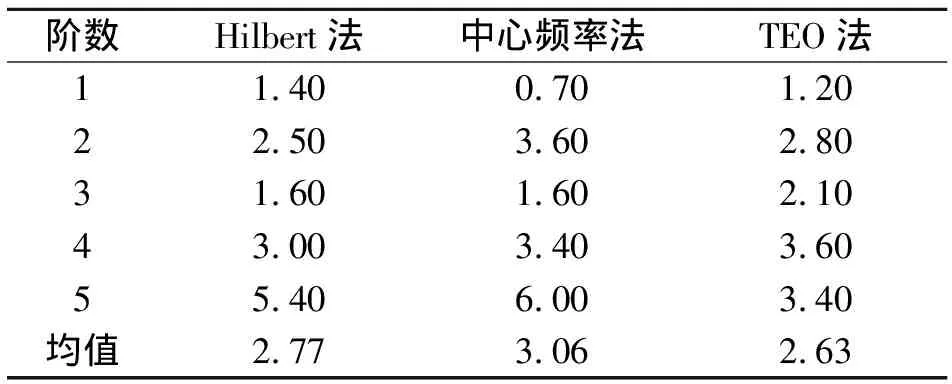
表2 固有频率误差

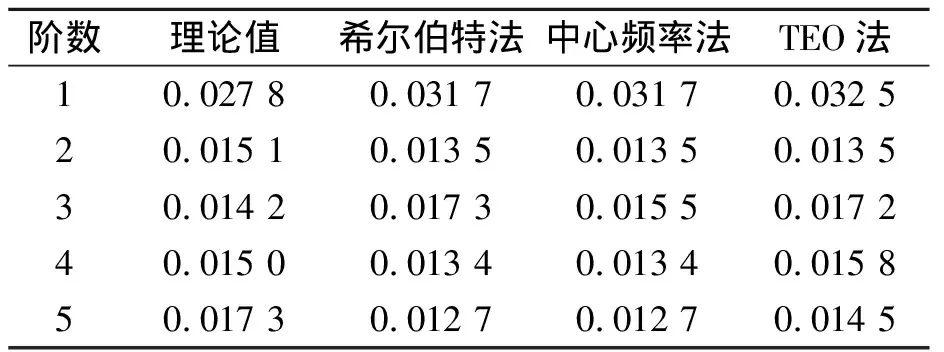
表3 仿真信号阻尼比

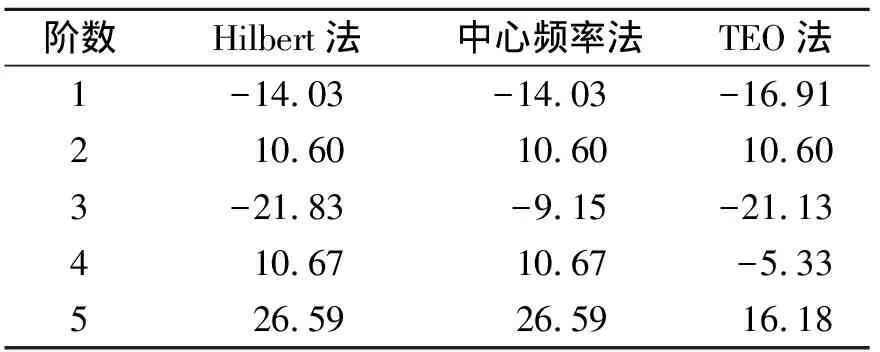
表4 阻尼比误差

3.3 VMD参数的影响

EMD是一种自适应的分解算法，但是过程总可能会产生虚假分量[6]。VMD分解依赖参数的选择，如图6所示，当罚参量α=128，随着层数参量增加，出现虚假的极点列，虚假的极点列中不会出现稳定极点，对于真实的模态结果，不会受到参数的影响。

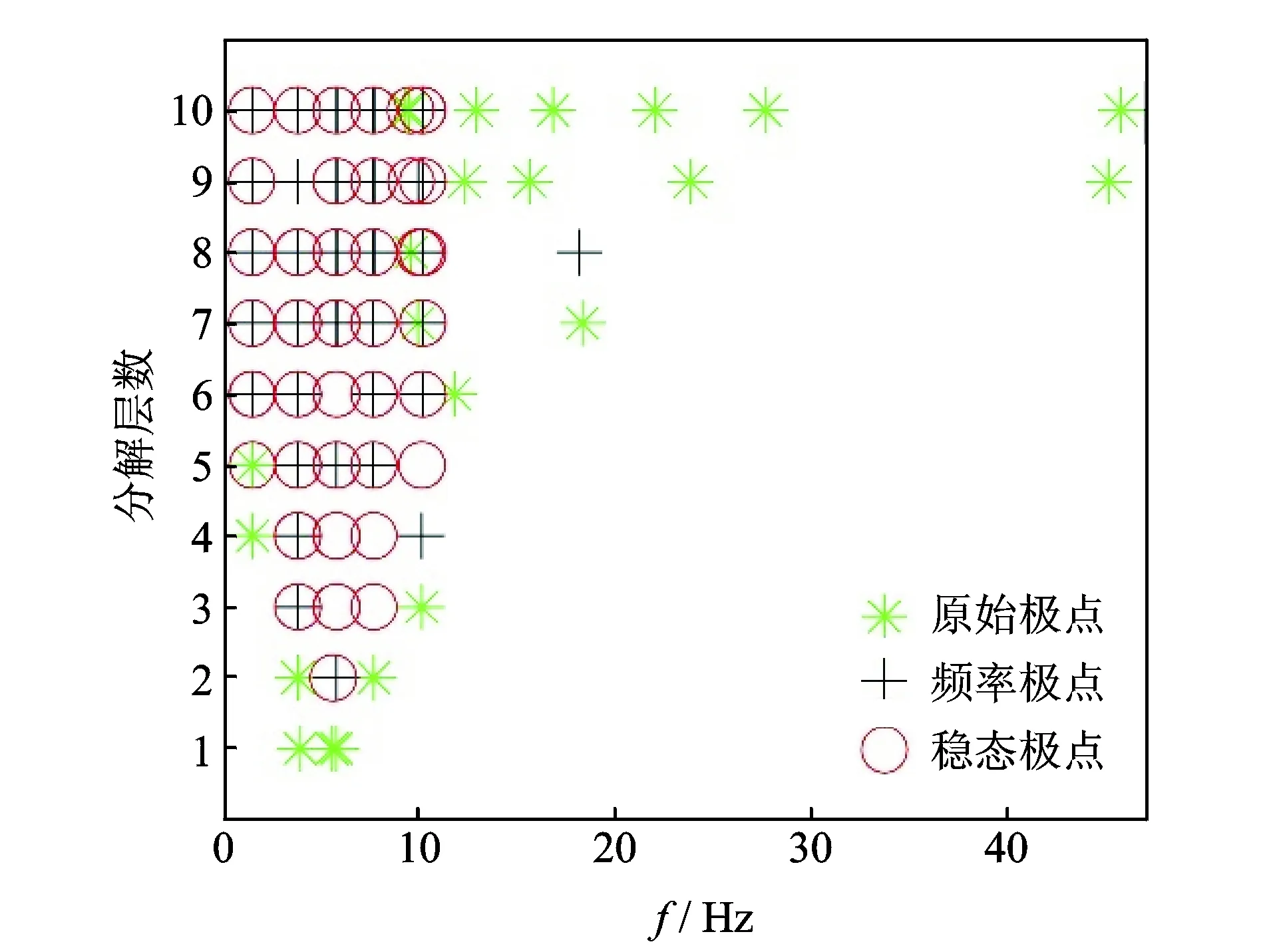
图6 α=64时TEO算法模态参数极点稳态图Fig.6 Modal parameter identification for TEO of stabilization diagram at α=64

选择不同的罚参量α，观察对结构系统参数识别的结果，如表5所示。5阶固有频率和阻尼比均达到稳定状态需要的层数，随着罚参量α的增加而增加。

通过观察仿真信号，不难发现，罚参量α不是最优参数时，会引入虚假分量，但是虚假分量的阻尼比不会稳定，层数参量K偏小时，无法得到全部模态频率，因此只需最大分解层数Kmax，真实的极点会形成稳定的极点列。由此可见，应用VMD的层数参量可以有效地帮助工程人员找到真实的模态固有频率与阻尼比，排除虚假分量。

表5 参量α与稳态层数关系

Tab.5 Relationship between parameterαand steady-state layer number

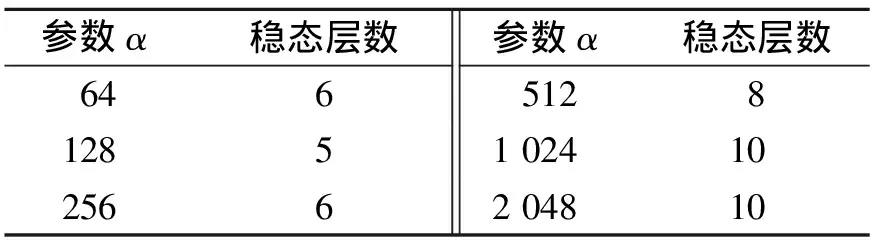
αα 646512 812851 0241025662 04810

3.4 测量噪声的影响

模态实验中通常信噪比在30～40 dB时可以确保结果的准确[17]，因此为了验证所述方法的鲁棒性，对仿真信号添加噪声，对信噪比10～40 dB的测试信号进行结构模态参数的识别。

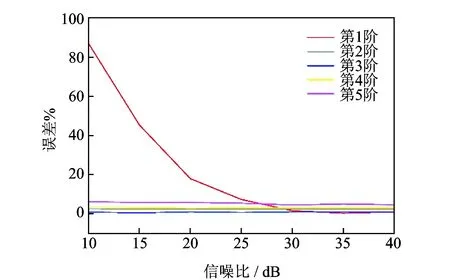
图7 固有频率的误差趋势Fig.7 Error of natural frequency

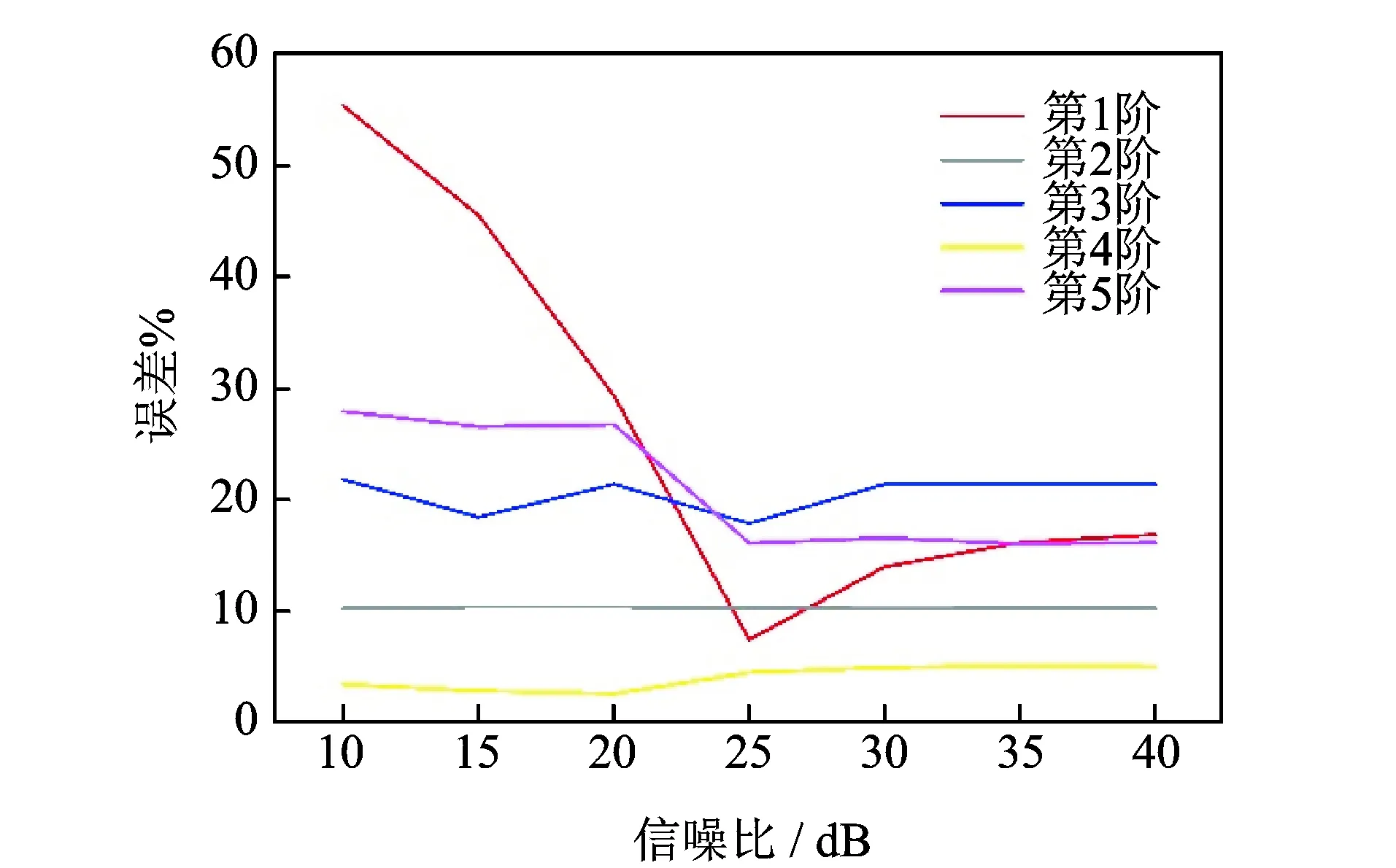
图8 阻尼比的误差趋势Fig.8 Error of damping ratio

如图7所示，估计得到固有频率除第1阶以外，固有频率误差趋势与信噪比关系不明显。图8所示阻尼与信噪比的误差趋势，同样除第1阶以外，与信噪比关系不明显。由此得出结论，本研究所提基于VMD与TEO的结构模态辨识方法具有较好的鲁棒性，计算效果良好。

4 实测算例

实测算例来自某动车组齿轮箱模态实验，如图9所示。动车组运行速度越来越高,其安全可靠性的要求就越来越高。齿轮箱作为动车组车辆传递扭矩驱动车辆行进的关键零部件,其安全稳定性直接影响动车组车辆的运行可靠性[18]。由于低阶模态对箱体的振动特性起主要作用，因此在持续工况时，齿轮箱箱体的固有频率应避开转动频率，避免共振现象。

图9 实验系统Fig.9 Experimental system

分别通过锤击法与环境激励两种方法进行实验，测点布置如图10所示，采样频率为5kHz，改进TEO算法中低通滤波阈值设为2kHz，分析频率分析范围为0～2 kHz。从所布置传感器的对立面的水平径向齿轮箱进行锤击实验，并采集敲击过程中的振动信号。环境激励时，选取齿轮箱从最高速减速至静止。

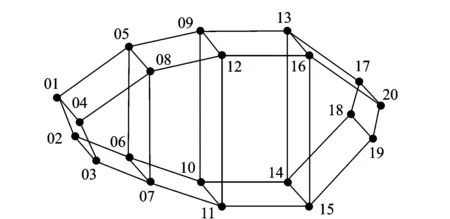
图10 齿轮箱测点布置Fig.10 Measurement setup of gearbox

从水平径向( 图9所示x方向) 对齿轮箱敲击并采集其振动加速度信号，时域信号如图11(a)所示，环境激励信号如图11(b)所示。利用VMD 对其进行分解，最大分解层数Kmax=20，罚参量设为α=5 000。应用改进的TEO算法得到每一层BIFM的固有频率与阻尼比，频率变化误差设为1%，阻尼变化误差设为5%，得固有频率与阻尼比的稳态结果如图12所示。

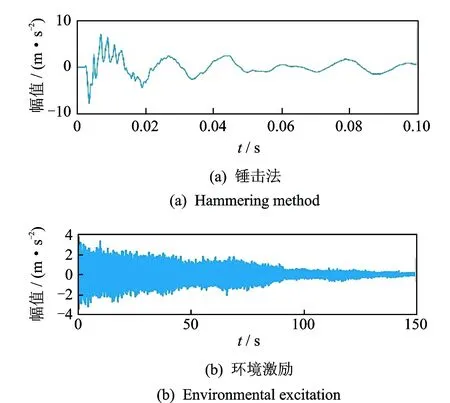
图11 时域波形Fig.11 Time-domain wave

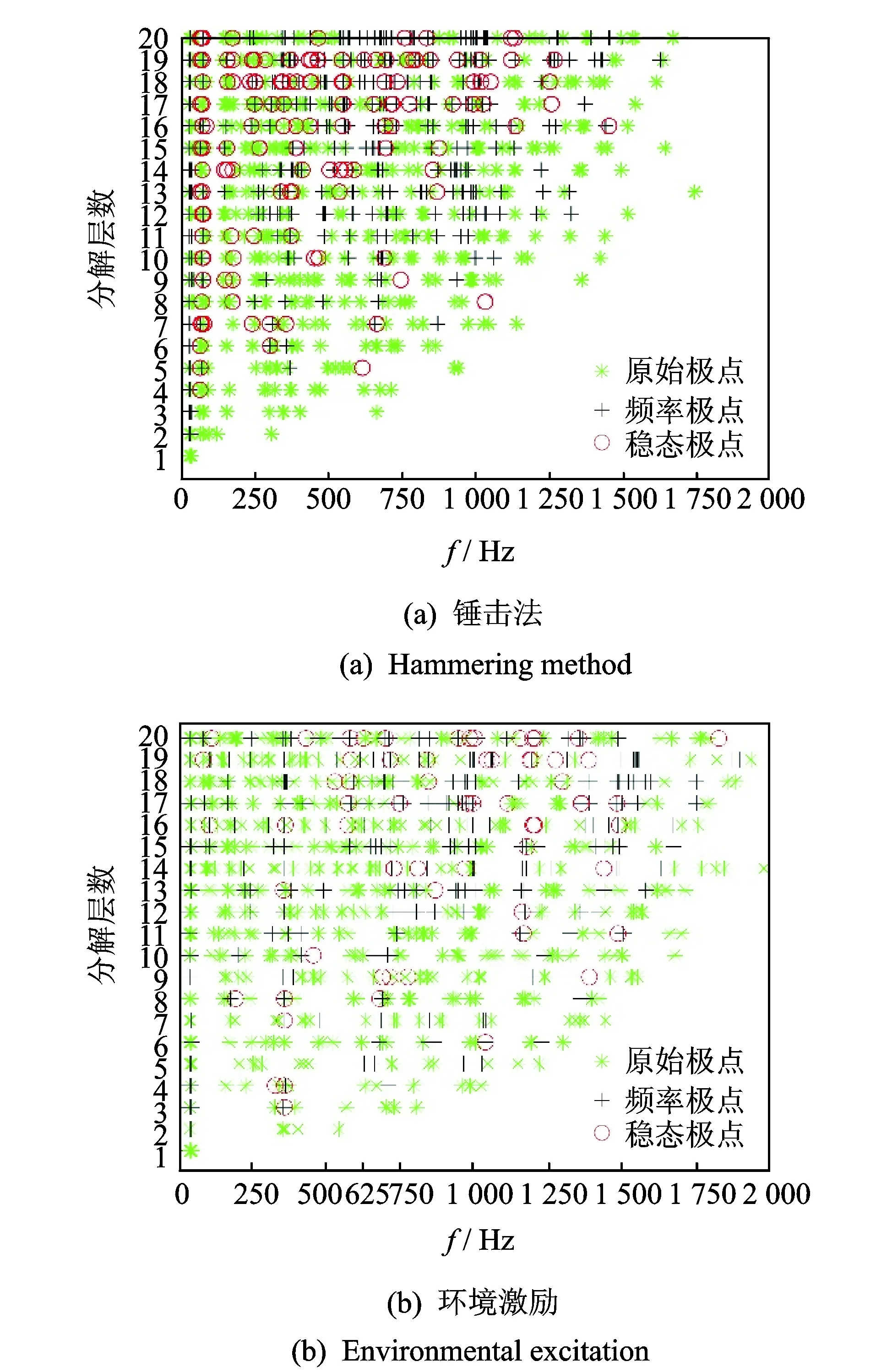
图12 齿轮箱稳态图Fig.12 Stability diagram of gearbox

由图12可看出，第1条明显的极点列及30 Hz附近，由于阻尼不满足阈值条件，没有稳态极点，因此不是齿轮箱固有模态频率。根据前述作法，找出极点列稳态极点，如表6所示为稳态极点组成的前7阶模态固有频率与阻尼比。

表6 信号前7阶固有频率与阻尼比

Tab.6 Signal In front of the seven order natural frequency and damping ratio

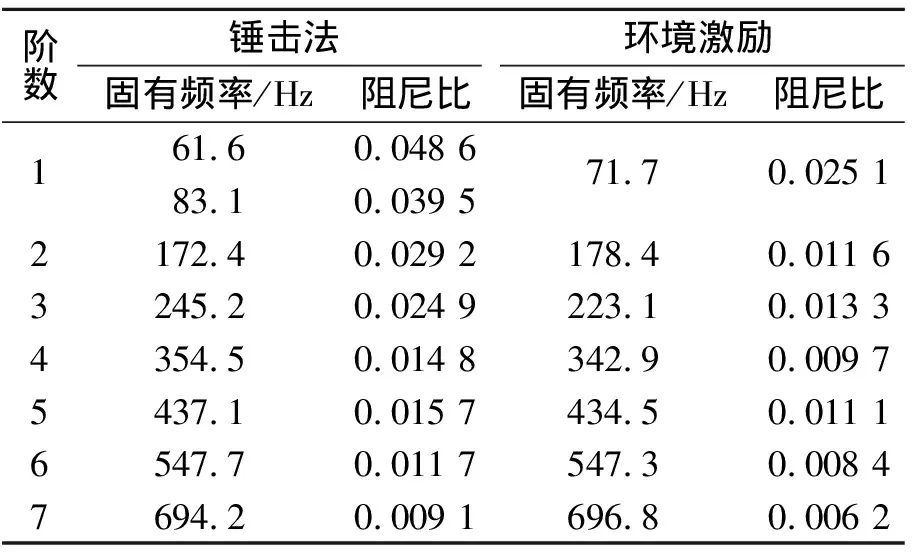
/Hz/Hz1 61.60.048 671.70.025 1 83.10.039 52172.40.029 2178.40.011 63245.20.024 9223.1 0.013 3 4354.50.014 8342.90.009 75437.10.015 7434.50.011 16547.70.011 7547.30.008 47694.20.009 1696.8 0.006 2

根据设计要求齿轮箱在持续工况时的小齿轮转速为4 174 r/min,车轴的转频为19.37 Hz，小于箱体的1阶模态频率(71.7 Hz)，而该工况下的齿轮对啮合频率为1 530.47 Hz，远高于前7阶固有频率。由于低阶模态对箱体的振动特性起主要作用，因此在持续工况时，齿轮箱箱体不会发生共振现象。

如表6所示，锤击法中60～80 Hz附近极点列随着K的增加出现频率分离，而环境激励法中仅存在一个稳态极点71.7 Hz。因此锤击法中识别的第1阶固有频率不能确定，而环境激励法中稳态极点十分确定。除第1阶固有频率不做评判，其他各阶识别结果偏差均小于10%，锤击法和环境激励法的模态分解结果基本一致。环境激励的阻尼比识别结果均小于力锤法30%～50%。由此可以得出，本研究所提方法适用于环境激励下的模态系统辨识。

5 结 论

1) 应用变分模态分解与Teager能量算子相结合分解提出了一种新的结构系统辨识方法：应用VMD得到满足TEO法的单一频率BIMF分量；通过VMD层数参量K的变化寻找稳态极点，作为模态固有频率与阻尼比的识别作法。

2) 通过改变层数参量K来寻找稳定的固有频率与阻尼比，解决了VMD参数选择这一方法缺陷。通过极点稳定的作法识别模态参数不仅适用于本研究所提的VMD-TEO识别方法，同时适用与VMD希尔伯特法与VMD中心频率法。通过仿真信号对比，所提方法将固有频率识别的平均误差降了0.14%。在不同白噪声情况下，本研究所提方法具有较好的鲁棒性。

3) 数值和实验结果表明，所提出的方法能够很好地利用各个模式的有限带宽进行信号分解，并准确地提取结构模态系统的固有频率与阻尼比。