基于Kriging模型的数控机床空间切削稳定性*
邓聪颖, 苗建国, 杨闪闪, 殷国富, 魏 博
(1.重庆邮电大学先进制造工程学院 重庆,400065) (2.四川大学空天科学与工程学院 成都,610065)
引 言
切削过程中出现的颤振失稳现象是恶化工件加工质量和加工效率、加速机床磨损和精度丧失的重要原因[1-2]。通常情况下,一般的铝合金等轻金属的高速切削稳定性主要受到刀具系统动力学特性的影响,而铸铁、钢等材料在粗加工与半精加工时的切削稳定性主要与机床主体结构动力学特性相关[3]。在加工过程中,刀具点空间位置的改变使机床整体结构随之变化,形成动态的整机质量矩阵、刚度矩阵和阻尼矩阵,引起机床动力学特性表征指标变化,进而使切削稳定性在整个加工空间发生演变[4]。因此,研究机床切削稳定性与加工位置的关联关系,有利于提高切削稳定性预测精度。
近年来,国内外许多学者研究了机床结构动力学特性与加工位置的关系[4-6],但是机床用户更关心面向加工过程的切削稳定性。Law等[7]采用模态选择准则对机床子部件进行简化,耦合各子部件构建机床整机动力学模型,通过更新结合面约束方程计算不同位置处刀尖点的频响函数,进而计算各位置的切削稳定性。杨毅青等[8]基于实验研究了机床沿不同进给方向以及机床主轴处于不同位置的颤振稳定域图预测,但是针对每个加工位置进行实验或仿真计算,需要较大的工作量。文献[3,9]结合实验设计、有限元仿真以及响应面模型,可计算机床任意位置的最小极限切削深度,但是在建立响应面模型时未考虑样本数据的空间相关性,也没有进一步探讨加工位置的优选方法。
笔者以机床加工点空间位置变化为研究基点,考虑切削稳定性表征指标的空间相关性,建立最小极限切削深度的Kriging预测模型,并采用改进粒子群算法确定具有最小极限切削深度最大值的加工位置。在此基础上,采用切削实验确定机床易颤振模态,进而基于能量分布理论确定机床薄弱结合部,通过提出结合部动刚度优化配置方案进一步提高最小极限切削深度值,以期更加精确地预测切削稳定性空间分异特性,并扩大稳定区域选择范围。
1 机床切削稳定性空间信息预测建模
1.1 机床空间切削稳定性概念
加工过程中切削力的动态变化量[10]可表示为
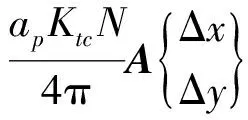
(1)
其中:ΔFx和ΔFy分别为x和y方向的切削力变化量;ap为轴向切削深度;Ktc为切向切削力系数;A为方向系数矩阵。
(2)
其中:Krt为径向切削力系数和切向切削力系数的比值;φst和φex分别为切入角和切出角;φjl为当前刀齿瞬时接触角。
在频域范围内分析式(1)可得
(3)
其中:F为切削力矩阵;G(iωc)为工件-刀具接触区域的传递函数矩阵。
当工件系统刚性较大时,通常采用刀尖点频率响应函数矩阵表示。式(3)的特征方程及特征值Λ为
(4)
根据式(4),极限切削深度aplim及主轴转速n为
(5)
采用图1所示的颤振稳定域叶瓣图描述式(5)中切削深度和主轴转速的关系,直线表示最小极限切削深度,其以下为绝对稳定区,在任意转速下选择该区域内的切削深度加工都不会发生颤振。针对一般较硬材料的粗加工、半精加工,切削过程中选择的主轴转速较低,对应的条件稳定区相对狭窄,因此通常选择在最小极限切削深度以下进行加工[3]。传递函数矩阵G(iωc)是绘制切削颤振稳定域图的关键。研究表明,G(iωc)受加工位置的影响,因此针对较硬材料在粗加工、半精加工阶段的切削稳定性准确预测问题,以最小极限切削深度aplimmin在加工空间的动态变化为研究对象,提出更为全面的广义最小极限切削深度函数
aplimmin=F(x,y,z)
(6)
其中:x,y,z分别为各向运动轴的位移。
基于式(6),进一步将aplimmin与加工位置的关联关系显性化,即可求解aplimmin在加工空间的演化规律。
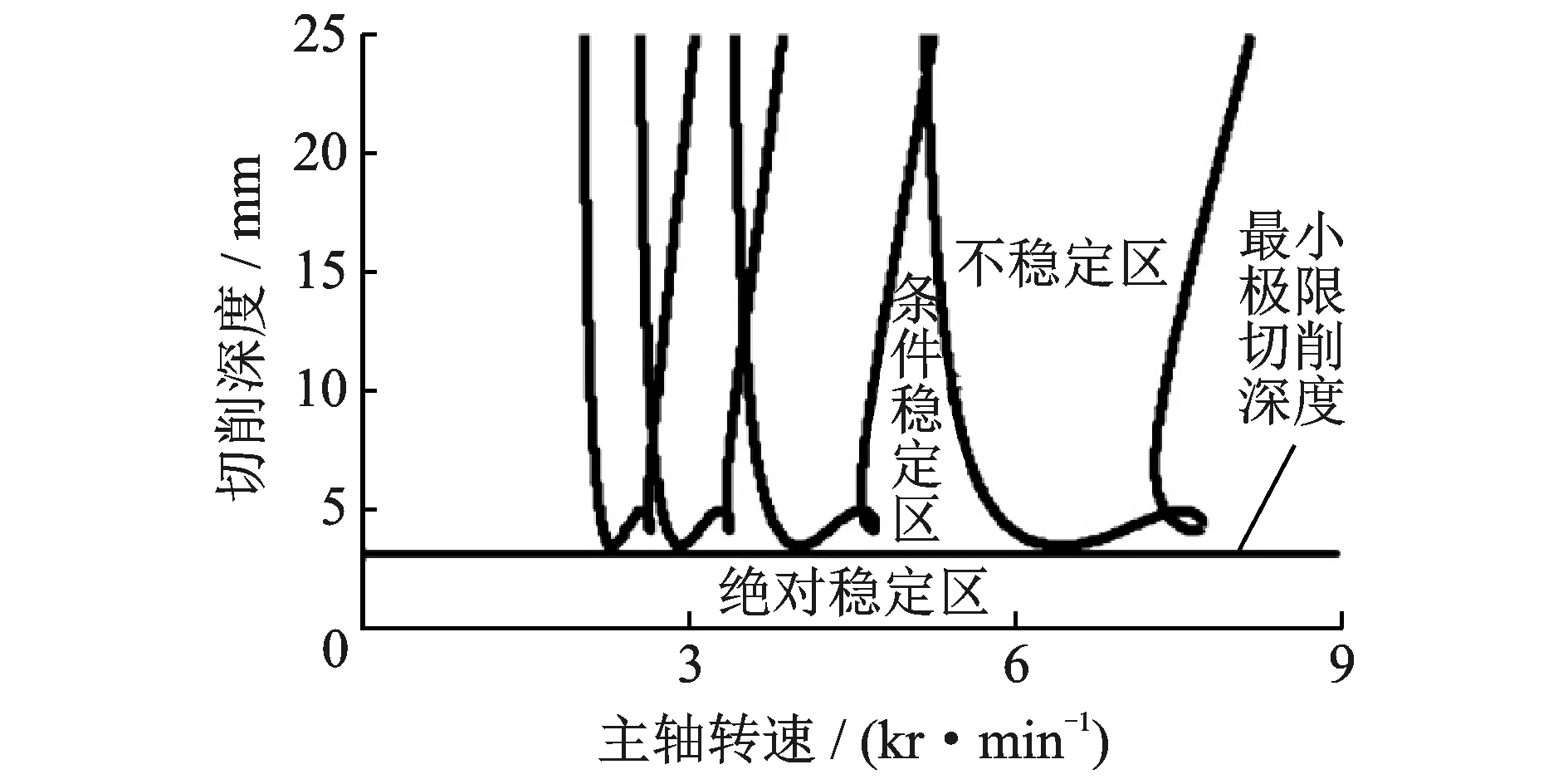
图1 颤振稳定域叶瓣图Fig.1 Chatter stability chart
1.2 广义最小极限切削深度Kriging预测模型
Kriging方法是基于已知样本信息的动态构造,从变量的空间相关性和变异性角度,构建对象问题的近似函数关系式,对非样本点信息进行无偏、最优估计[6,11]。该方法包括线性回归部分和非参数部分,通常Kriging近似模型具有如下表达
(7)

协方差矩阵可表示为
cov(z(xl),z(xj))=σ2R(xl,xj)
(8)
R(xl,xj)为样本空间中任意两个样本点xl和xj的空间相关函数,目前广泛采用高斯函数和指数函数表达,它决定了模拟的精度,依次具有如下形式
(9)
其中:参数θk为待定参数;xlk,xjk为样本点xl,xj的kth分量。
根据实验样本点及其对应的响应值,形成一个相关矩阵
(10)
采用加权最小二乘法,得到Kriging模型的回归系数矩阵
(11)
基于样本点xs的响应值Y的线性加权差值来预估待测点x的响应值
(12)
近似值与真实值之间的误差为
(13)
将式(9)、式(10)的函数代入式(13),可得
基于无偏差预测要求
(15)
式(15)的均方差为
(16)
结合上式与方差最小条件、拉格朗日乘子法
(17)
综上,Kriging模型可最终表达为
(18)
其中:γ*=R-1(YT-Fsβ*)。
为检验Kriging模型的预测精度,采用设计空间任意样本点的相对误差(RE)与平均相对误差(ERR)两个标准[14]来评价
(19)
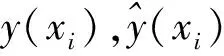
如果RE与ERR的值越接近0,则表明Kriging模型的精度越高。
构建广义最小极限切削深度Kriging预测模型的主要流程如下:
1) 采用实验设计方法离散化机床工作空间,确定样本点的空间位置坐标(xi,yi,zi),并通过实验获取各样本点位置对应的频率响应函数G(iωc)i;
2) 绘制各样本点位置对应的颤振稳定域叶瓣图,进而确定各样本点位置的最小极限切削深度;
3) 基于式(7)~式(18)构建广义最小极限切削深度的Kriging预测模型
aplimmin(x,y,z)=fT(x,y,z)β+rT(x,y,z)γ*
(20)
4) 求解新样本点处的最小极限切削深度,结合式(19)、式(20)检验步骤3中Kriging预测模型的精度,根据验证结果调整模型,提高拟合精度。
2 基于Kriging预测模型的广义空间切削稳定性优化问题描述
本研究中广义空间切削稳定性优化问题是在给定切削宽度和进给量的基础上,基于式(20)建立的最小极限切削深度Kriging预测模型,寻求具有较高最小极限切削深度值的加工位置,并在此基础上进一步提高最小极限切削深度值,扩大切削参数选择范围。
2.1 改进粒子群优化算法
粒子群算法作为一种机器学习的群体智能优化算法,能有效实现非线性和多峰值复杂目标的优化[12]。在D维空间中,假设n个粒子组成一个群落,每个粒子的特性通过位置Xi=(xi1,xi2,...,xiD)、速度Vi=(vi1,vi2,...,viD)以及适应值fi来表征。每一个粒子位置对应该优化的一个潜在解,速度表征粒子当前的飞行方向和距离,适应度值则采用适应度函数计算,表示粒子在当前位置的优劣性。每个粒子的位置更新取决于个体极值Pbset和群体极值Gbest的变化,同时更新适应度值,通过分析新粒子、个体极值和群体极值的适应度值,进一步更新个体极值与群体极值。位置与速度按下式更新
(21)
其中:ω为惯性权重;i为第i个粒子,i=1,2,…,n;d为维数,d=1,2,…,D;c1和c2表示速度加权因子为0或正的常数;r1和r2为[0,1]之间的随机数。
惯性权重ω的设置对粒子群算法的求解极为重要,为更好地满足实际要求,迭代求解过程中基于粒子不同的特性,动态调整惯性权重ω。假设全部粒子平均适应度以favg表征,fmax为本轮迭代中的最大适应度值,fhavg代表适应度值大于favg的粒子的平均适应度值,则迭代过程中按如下方式动态调整ω[12]:
1) 当fi≤favg时,优先考虑提高该类粒子的全局搜索能力,应设置较大的ω
(22)
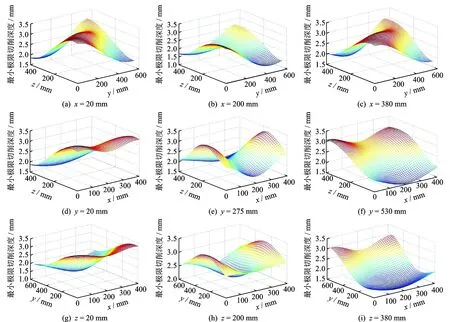
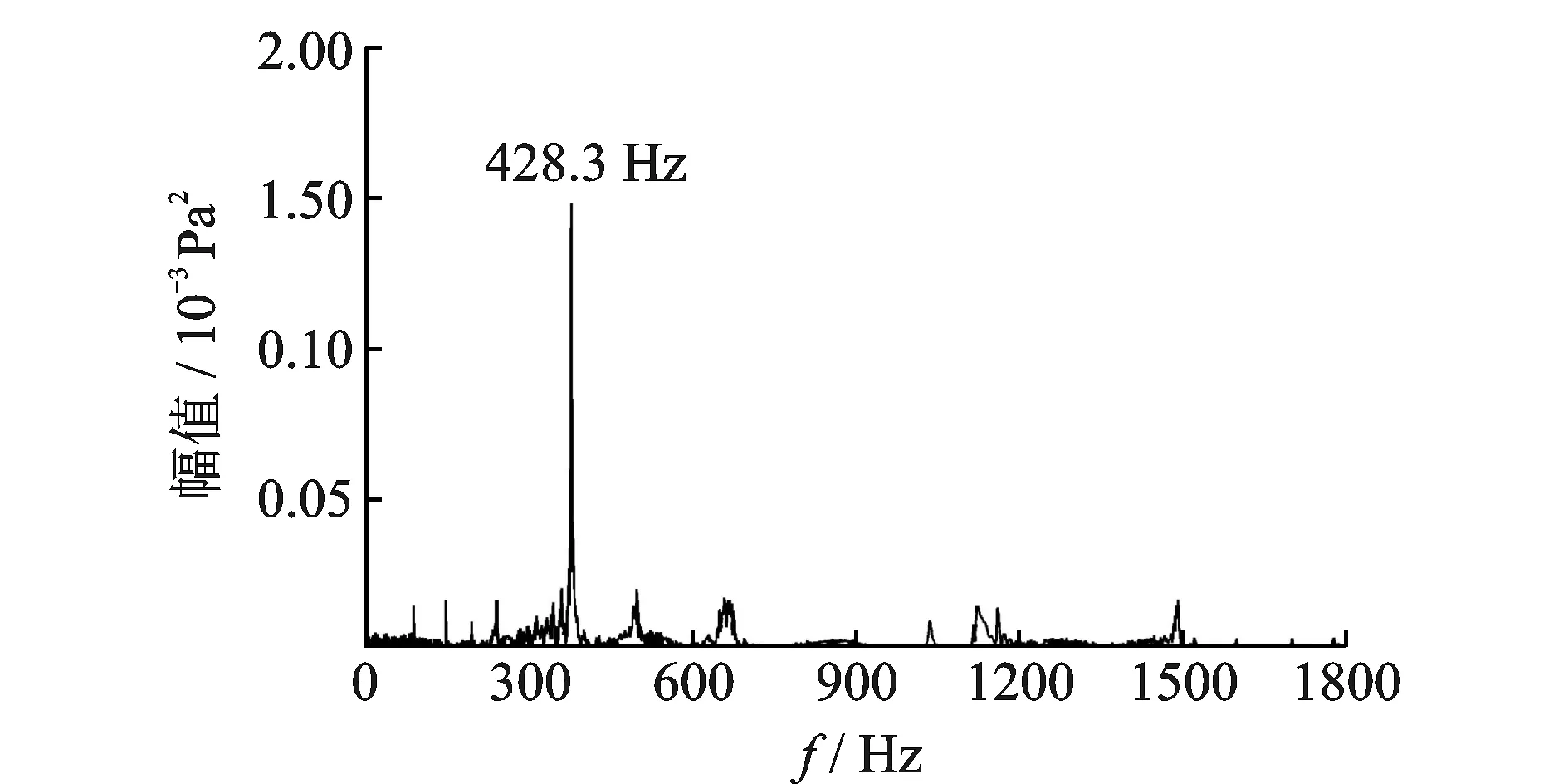
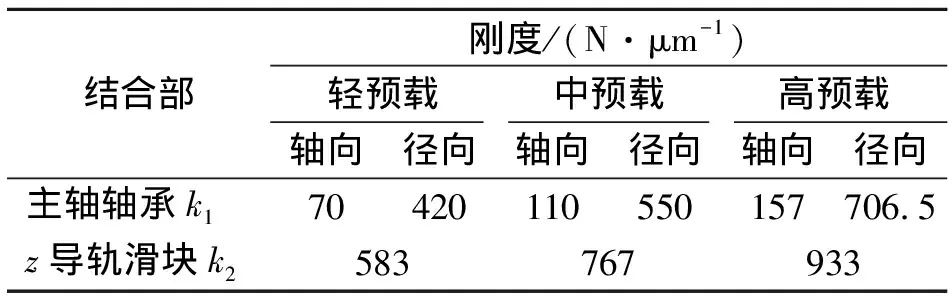
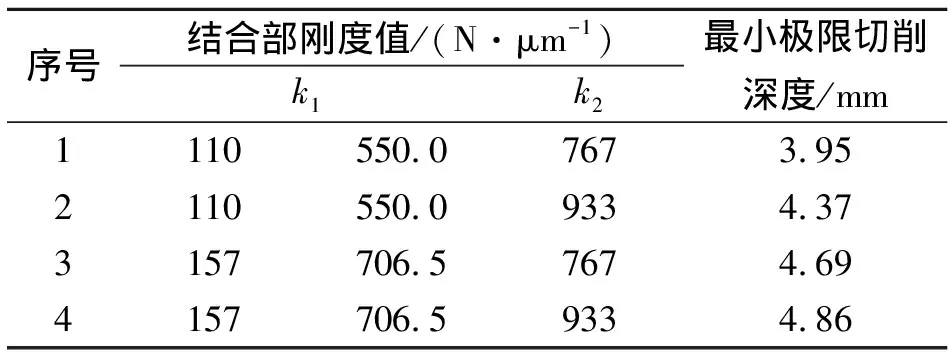
2) 当favg (23) 3) 当fhavg (24) 式(22)~式(24)中,右侧ω值遵循线性递减规律,k为当前迭代次数,kmax为初始化最大迭代次数 (25) 为避免粒子群算法出现早熟收敛,采用变异算子的形式对粒子群算法中某些变量以一定概率重新初始化 (26) 以加工点各向位移x,y,z为变量,最小极限切削深度的最大值为目标,结合式(23)~(26)可建立刀具点加工位置寻优模型,并按图2所示流程求解。 图2 改进粒子群算法流程Fig.2 Improved particle swarm optimization algorithm 在2.1节确定的机床最优加工点位置附近进行切削时,为扩大切削参数选择范围,提高切削效率,从机床结构动力学特性和切削稳定性关联关系角度进行切削稳定性优化。考虑机床振动问题60%以上来源于结合部,且结合部动刚度特性研究比阻尼特性研究更易实现,笔者结合切削实验和能量分布理论,确定机床易颤振模态及对应的薄弱结合部,通过优化薄弱结合部动刚度来提高机床加工点动刚度,进而提高最小极限切削深度。 首先以2.1节中求解的最小极限切削深度的最大值为基准,线性递增作为切削深度并进行切削实验,采用麦克风拾取加工过程的声音信号,根据声音信号的频谱分析确定机床易颤振模态。在此基础上,采用能量分布理论分析机床在易颤振阶模态振动时弹性能在整机中的分布情况。假设系统由N个模块构成,其中第m个模块在i阶模态振动时,系统与模块m的弹性能[13]可表达为 (27) 其中:VAi,Vmi分别为系统在第i阶模态振动时系统与模块m的弹性能;Ai为i阶模态下模块m所有自由度的幅值向量;Ki为模块m的刚度矩阵。 模块m在系统中的弹性能分布率Ri定义为 (28) 机床在易颤振阶模态振动时,如果计算的结合部Ri值越高,则表明该结合部刚度越低,需要对其进行优化设计。 图3为广义空间切削稳定性优化流程,首先,基于构造的样本信息在Matlab环境中建立最小极限切削深度Kriging模型,并结合改进粒子群算法求解最优加工位置及最小极限切削深度;其次,采用切削实验和弹性能分布率确定机床易颤振模态下的薄弱结合部,提出其动刚度优化方案,进而计算整机模态和切削稳定性,获取各薄弱结合部动刚度最优配置以及优化后的最小极限切削深度值。 图3 广义空间切削稳定性优化的实现Fig.3 Optimization of cutting stability in generalized space 将提出的广义空间切削稳定性优化方法应用于普瑞斯数控机床厂的一台三轴立式加工中心,如图4所示。针对该机床耗时最多的某铸件的粗加工、半精加工阶段,采用的切削深度仅为2.42 mm。为提高加工效率,结合理论分析与图3,对该工序的最小极限切削深度进行优化。 工作台、床鞍以及主轴箱的行程依次为x-400 mm,y-400 mm和z-550 mm。笔者结合中心复合表面设计和Box-Behnken实验设计法规划样本点空间位置,如表1和图4所示。各样本点位置对应的刀尖点频率响应函数(frequency response functions,简称FRF)由锤击法模态实验获取,进而通过式(1)~(5)计算对应的最小极限切削深度aplimmin。 采用图4中实心标记的27个空间点作为位置变量输入,关联的aplimmin作为输出,选择随机函数z(x,y,z)协方差计算模型为高斯函数,获取正则化θ参数(θx=0.825,θy=0.625,θz=0.825),完成Kriging预测模型构建。为验证该模型的准确性,首先,采用该模型预测图4中空心标记的6个加工位置的aplimmin;其次,在该6个位置进行切削实验,刀具为直径20 mm、螺旋角45°的4齿硬质合金立铣刀,工件材料为45钢,主轴转速为3kr/min,径向切削宽度为14 mm,进给速度为0.06 mm/z。通过磁力座将PCB公司测量范围为4 Hz~20 kHz的探头型传声器固定在工作台上,拾取切削过程的声音信号并进行频谱分析,确定颤振及对应的aplimmin,其采样频率为6 kHz。根据式(19)获取由表2给出的样本点实验值和预测值的相对误差(RE)与平均相对误差(ERR),其中RE最大值为3.12%,ERR最大值为2.03%,可见建立的Kriging预测模型拟合精度较高。 /mmxyz/mm/mmxyz/mm/mmxyz/mm13805303802.991020202002.7919380530201.9323802753801.8711202752003.2220380275202.673380203801.9812205302002.632138020203.324200203801.64132005302002.312220020203.0952002753801.73142002752002.1923200275201.8462005303802.6115200202002.6824200530201.537205303803.0716380202002.812520530201.978202753802.09173802752003.172620275202.64920203801.82183805302002.79272020203.46 表2 精度检验样本点相对误差 图5描述了最小极限切削深度aplimmin在加工空间的演化规律,由图可以看出,aplimmin随加工位置变化而改变。图5(b)中,y-z轴联动时,aplimmin最低为1.47 mm,最高为3.10 mm,变化率达111.7%;图5(e)中,x-z轴联动时,aplimmin最低为2.15 mm,最高为3.27 mm,变化率达52.0%;图5(h)中,x-y轴联动时,aplimmin最低为1.74 mm,最高为3.30 mm,变化率达89.4%。分析图5(a~c)发现,当y-z轴坐标确定时,工作台x向位置的变化对aplimmin的影响相对较小。上述研究表明,在规划机床切削工艺时,应尽量使机床处于具有较高切削深度且其变化率较小的加工区域,并且应优先使用极限切削深度变化较小的运动方式来保障机床加工的平稳性。 图5 最小极限切削深度在加工空间的演化规律Fig.5 Evolution law of minimum limit cutting depth in machining space 采用改进粒子群算法获取使最小极限切削深度值最大化的加工位置,首先设置基本参数如下:初始化种群规模为100,以加工点各向位移x,y,z为变量,种群中每个粒子的维数为3,粒子的位置和初始速度随机给定,更新过程按式(22)~(25)进行,根据式(20)建立的Kriging预测模型计算粒子的适应度值,每次更新后采用式(26)进行变异操作,并重新初始化粒子。按照图2的求解流程,计算的加工空间aplimmin最大值为3.47 mm,对应的最优加工位置为30.77,14.12,36.78 mm。 在最优加工位置附近进行切削实验,通过切削中声音信号的频谱分析确定颤振频率分布范围为406~443 Hz(如图6所示的切削深度为4.00 mm时声音信号的频谱)。由于颤振常常出现在系统某阶固有频率附近,可根据机床整机模态信息判断机床易颤振模态由第10阶模态(423.7 Hz)引起,对应模态振型表现为主轴-立柱系统绕y轴的摆动。因此,以该系统中z向主轴轴承结合部、z向滚珠丝杠结合部、z向导轨滑块结合部以及床身-立柱结合部为研究对象,根据式(27)、式(28)计算出各结合部弹性能分布依次为26.04%,6.58%,32.80%和3.91%,从而判定主轴轴承结合部、导轨滑块结合部为较薄弱结合部,并以该类结合部动刚度为优化变量。 图6 切削过程中声音信号频谱图Fig.6 Spectrogram of sound signal in cutting process 主轴与直线导轨系统均为外购件,并且其待优化结合部均为轻预载,因此根据产品技术手册和课题组结合部动力学特性辨识成果,基于表3中的中预载和高预载情况下的结合部动刚度,按照表4的优化方案依次将其写入处于最优工位的机床整机有限元模型中,以进行谐响应分析获取各组刀尖频响函数矩阵,采用式(1)~(5)计算各aplimmin。由表4看出,aplimmin由初始的2.42 mm提高到4.86 mm,增幅为100.8%,验证了笔者提出的广义空间最小极限切削深度优化方法的有效性。 表3 薄弱结合部刚度数据 /(N·μm-1)k1k2/mm1110550.07673.952110550.09334.373157706.57674.694157706.59334.86 1) 基于Kriging方法理论建立最小极限切削深度的空间信息预测模型,研究其在加工空间的演化规律,融合了机床运动部件位姿的随机组合对切削稳定性的影响,有利于在完整加工空间中准确描述切削稳定性,提高了切削稳定性预测精度。 2) 结合最小极限切削深度Kriging预测模型与改进粒子群算法,可有效确定使最小极限切削深度最大化的加工位置,并在此基础上引入切削实验和弹性能分布理论,优化机床在易颤振模态下薄弱结合部的动刚度配置,进一步提高了最小极限切削深度,也为机床厂家外购件的选择提供了技术支持。 3) 采用提出的机床空间切削稳定性研究方法,可进一步探讨轴向极限切削深度、主轴转速、切削宽度等切削稳定性关联指标与加工空间的关联关系,为更全面和更准确地进行切削加工参数选择和工艺规划提供理论依据和数据支持。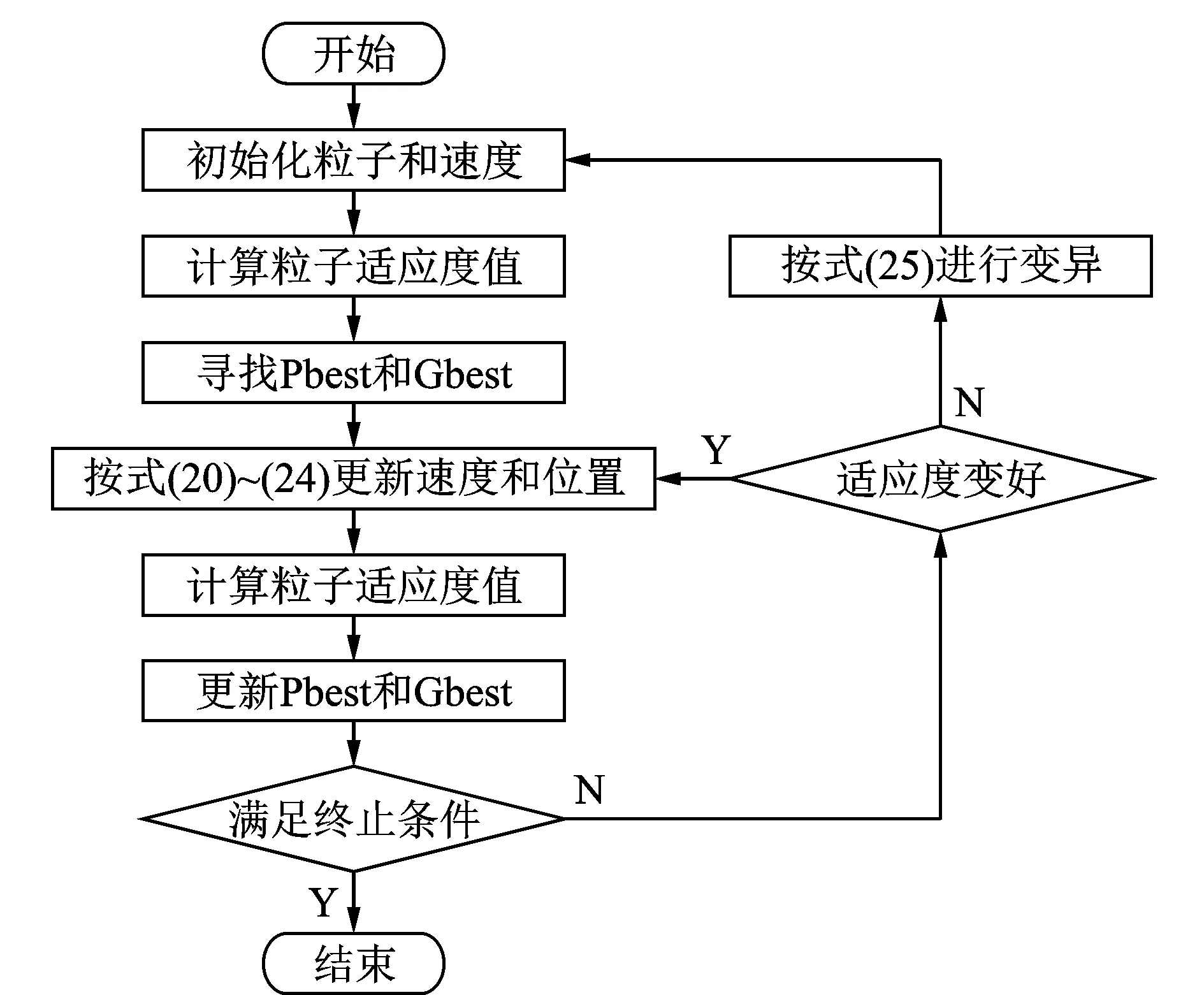
2.2 基于能量分布的切削稳定性优化
2.3 广义空间切削稳定性优化的实现
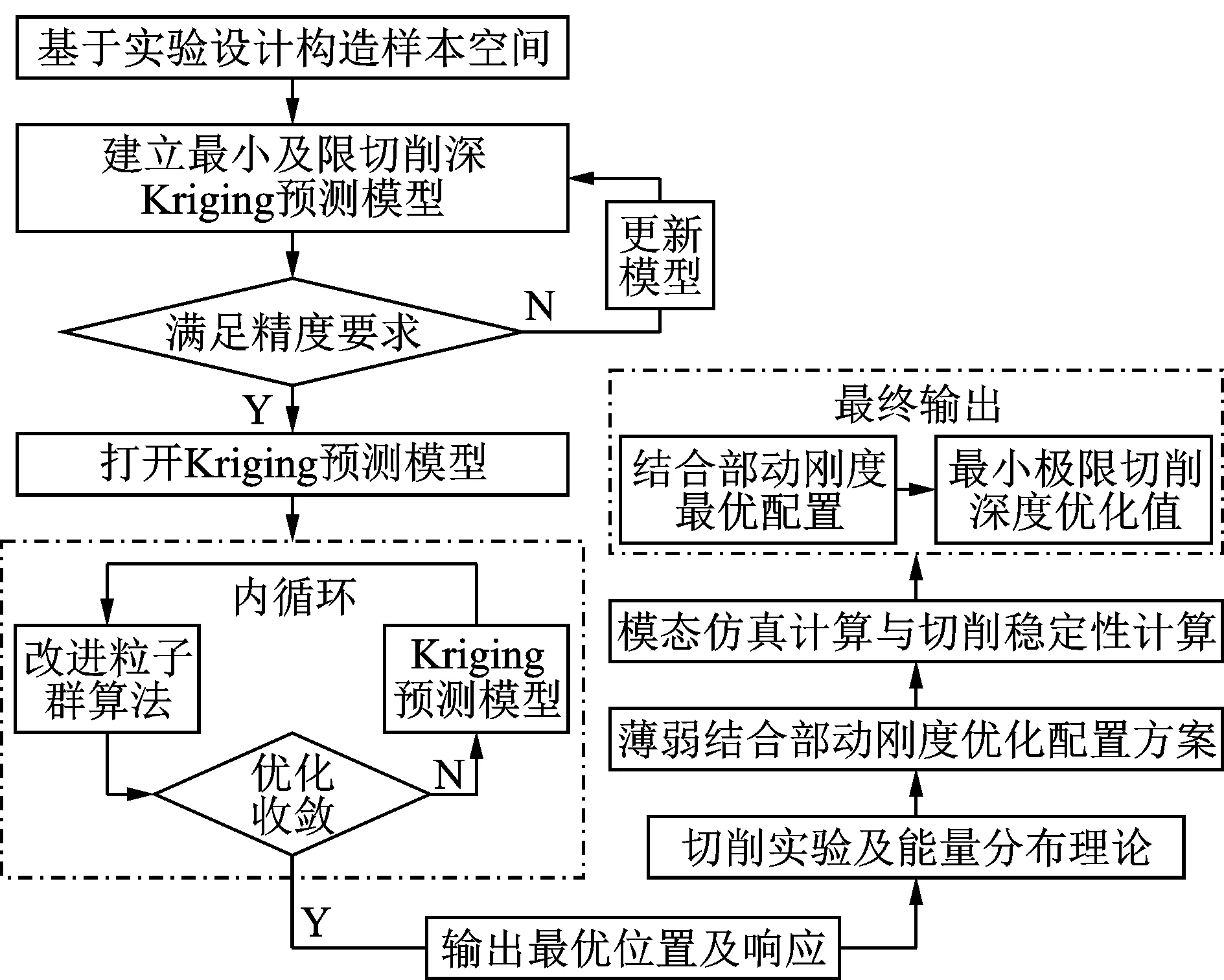
3 基于Kriging预测模型的广义空间切削稳定性优化实例
3.1 广义最小极限切削深度Kriging模型构建
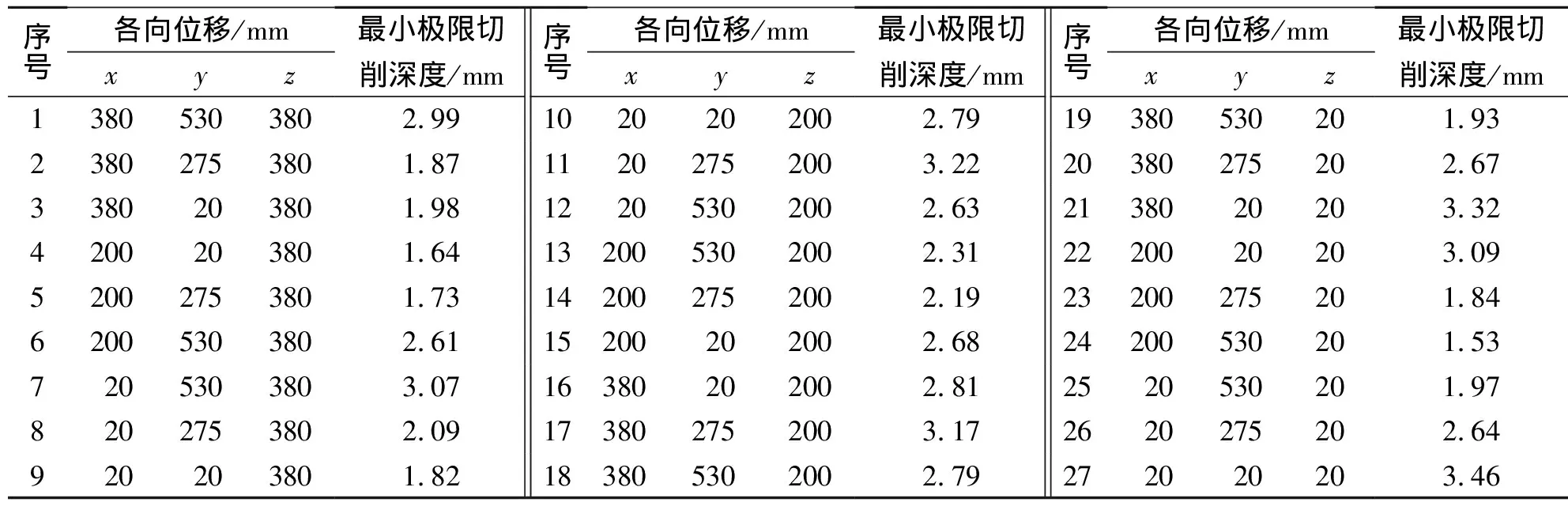
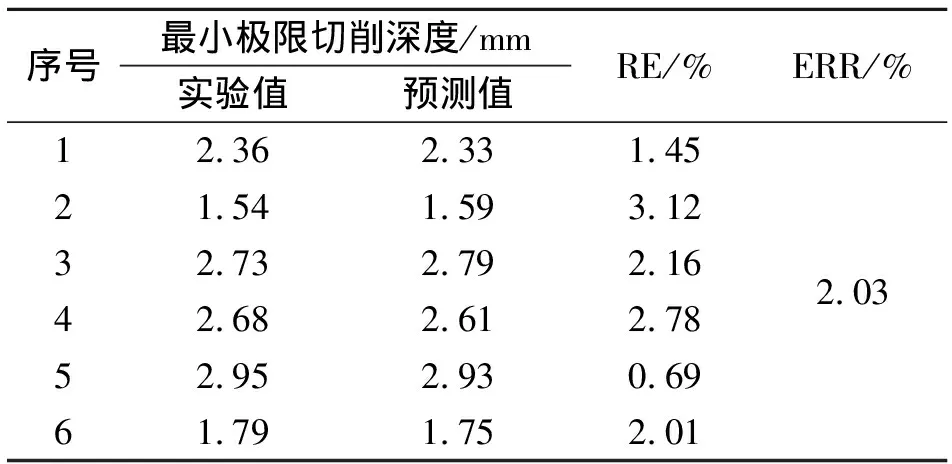
3.2 广义最小极限切削深度动态优化
4 结 论

