赏析多元解法 优化教学策略
——一道中考试题的解法分析及其教学启示
陈 锋
(江苏省无锡市太湖格致中学)
章建跃教授认为,数学教育的核心是对学生进行数学思维和语言的教育,即通过数学阅读、运算、推理和表达的训练,使学生正确理解数学知识,形成用数学知识合理解释,直至创造性地解决问题的能力.
江苏省无锡市2017年中考试卷的第27题是一道渗透着命题者思想和智慧的试题,不仅体现了对学生综合能力的考查,也展示了对教师教学情况的阶段性考量.虽然此题的题型对于大多数学生来说并不陌生,但从阅卷反馈的情况来看,不同层次的学生得分差异较大.下面,笔者结合学生对此题的解答,在分析学生解答的同时,谈一谈笔者的思考.
一、试题呈现
如图1,以原点O为圆心、3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过点P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC∶CE=1∶2.
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.

图1
二、试题解析
江苏省无锡市的中考试题一贯紧扣《义务教育数学课程标准(2011年版)》,能够给教师的教学带来明确的指导方向.概念教学扎实,课堂上注重思维的训练,以生为本,在形式上不是简单套用以往的模式,这些特点在此题上得到了很大的体现.
此题第(1)小题的解答是完整解题的关键,如果第(1)小题能顺利完成,第(2)小题就比较容易求解.从学生的答题情况来看,第(1)小题解法多样,各种解法难易程度不同,而第(2)小题的解法比较单一,因此,如何突破第(1)小题成为此题求解的关键.下面笔者就学生对此题第(1)小题的解法进行展示和分析.
三、解法展示
1.利用已有条件,直接建立方程,展示数学解题的直观性
从已有的图形条件来看,此题可以看作是圆在直角坐标系中的运用,如果能在解题之前仔细研究图形信息,加强对图形的认识与理解,分析图中存在的等量关系,充分思考已知与未知之间的关系,那么就可以利用已有条件,直接建立方程.
解法1:利用圆的基本性质求解.
如图2,连接AD,OC.
由圆的性质,得
AC=AD,∠COP=∠EAD,∠CPO=∠EDA=90°.
所以△COP∽△EAD.
所以OP∶OC=AD∶AE=1∶3.
由此可得OP=1.
所以点P的坐标是(1,0).
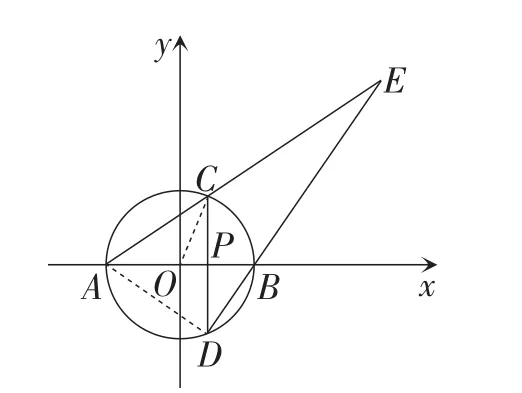
图2
解法2:利用圆中的基本图形求解.
如图3,连接BC,AD,图中出现圆中常见的基本相似三角形,即△EBC∽△EAD.
由圆的对称性,得AC=AD,∠EDA=∠ECB=90°.

则EC=2k.

由cos∠CAB=AC∶AB=AP∶AC,
得AP=4.
所以点P的坐标是(1,0).

图3
解法3:利用代数解析法求解.
如图4,过点E作EH⊥Ox,交x轴于点H.
设点C(m,n),
则D(m,-n).
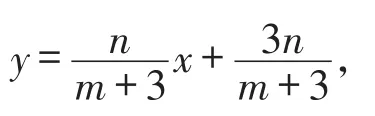
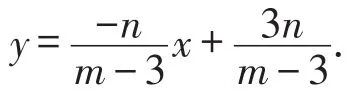

由AC∶CE=1∶2,
可得AH=3AP,
解得m=1,m=-3(舍).
所以点P的坐标是(1,0).
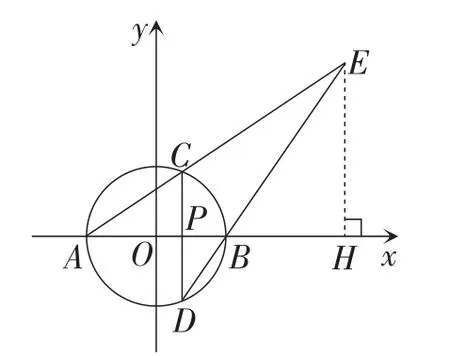
图4

2.转换已有信息,间接构造方程,体现数学解题的思维性
此题是平面直角坐标系背景下包含圆、三角形、线段比例、函数等知识的综合题,面对试题中同时呈现出来的信息,必须对每个信息有所思考、分析,并对其进行转换,从而选择最合适的解题思路.此题的绝妙之处就在于以试题所给的任何一个信息作为突破口都能顺利进行解答,因此,解题的关键在于得到什么信息,往哪个方向思考,怎样转化信息.
解法4:通过平行转化求解.
如图5,连接BC,过点E作EH⊥Ox,垂足为点H.过点C作CG∥Ox,交DE于点G.
由此可得△APC∽△AHE.
所以AP∶PH=1∶2,PC∶EH=1∶3.
由条件可知,△CPB∽△EHB.
从而得到BP∶BH=1∶3.
所以PH=4BP,
即AP=2BP.
因为AB=6,
所以AP=4.
所以点P的坐标是(1,0).
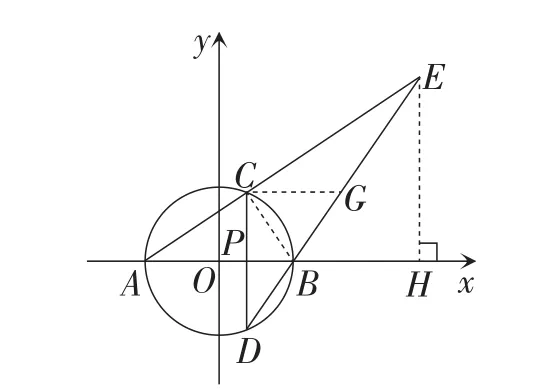
图5
解法5:通过坐标转化求解.
设点P的坐标为(a,0),则AP=a+3,BP=3-a.
所以a+3=2(3 -a).
解得a=1.
所以点P的坐标是(1,0).
解法6:通过相似转化求解.
如图6,连接OC,过点E作EH⊥Ox,垂足为点H.
由同弧所对的圆周角相等,得∠ACD=∠ABD.
因为∠ABD=∠EBH,
所以∠ACD=∠EBH.
所以△ACP∽△EBH.
所以AP∶EH=CP∶BH.
由AC∶CE=1∶2,
可知PH=2AP,EH=3CP.
设OP=a,

解得a=1,a=-3(舍).
所以点P的坐标为(1,0).

图6

解法4通过平行线转换已知条件AC∶CE=1∶2,将其作为突破口进行计算.同样的也可以利用平行线的性质得到CG∶AB=2∶3,BP∶CG=1∶2,AB=3BP=6,BP=2,亦可解得点P的坐标为(1,0).解法5则通过坐标转化求解,求点坐标一般会考虑将其转化为求水平或垂直的线段长,在直角坐标系中也常用设坐标得线段的方法进行转化.解法6通过相似转化求解,根据比例关系找到图中隐藏的相似图形,利用相似将相应线段的比例关系进行转换,此方法简洁明了.
四、教学建议
1.教学中强化解题步骤的必要性
此题解答的关键在于要抓住题干和图形中的有效信息,在对相关信息进行适当的转化后,解题的思路也就开阔了.由此可见,在平时的教学过程中,首先,教师要留给学生充足的时间仔细审题,让学生了解题目的已知条件、已有数据、已有图形和求解目标,明确解题目标.其次,要让学生反复研读条件,这样其才能理解题意,进而理清题目目标和条件之间的逻辑关系,以及解题所需要的路径和方法,并找到它们之间的因果关系以及因果关系之间的关联所在.最后,再进行有条理、有层次、有系统的解答.只有这样,教师才能潜移默化地引导学生主动的去感知、发现、探索,从而帮助学生建立数感和图感,积累经验,形成良好的品质.可见只有让学生认清仔细审题的重要性,才能让其亲身感悟数学知识的转化过程,感悟运用数学知识形成解题方法的过程,进而做到“知其然,更知其所以然”.
2.教学中注重思考拓展的重要性
虽然题中所给的图形是静态的,但是读题后学生大脑中的条件却是动态的,是可以转化和拓展的.正因为如此,教师在课堂上讲解、训练综合题时,首先,要注重对学生进行读题标图思考的训练,指导学生对某些已知条件进行发散性的思考,思考其还能生成哪些条件,清楚连接各种条件的常用纽带和方法是什么,同时对于学生不同的思考方向要有不同的预设,学生的解法是自然生成的,教师要跟着学生的思路进行分析,也要适时对学生的方法进行有效的调整,让其思维更加清晰,方法更加简洁.其次,要根据学生的思考方向给予一些方法上的指导,在适度一题多解的同时,不要忘了引导学生进行反思、对比、优化,使其找到思路自然、简便的解法.中考解答题一般都有多种解题方案,如此题的解法较多,添加辅助线的方法也很多,看见圆可以连接半径,由求坐标想到作垂线.但是这两条辅助线分归各自的条件,这些条件通过什么方法才能联系在一起呢?根据圆的对称性找到相等的边或角,借助比例、相似,以及三角函数寻找已知与未知线段之间的关系,线段与点坐标之间的关系,则可以通过设未知数来解决,等等.要想在较短的时间内做出科学的决策,并选择简洁的方法,靠的是平时的相关训练和点滴积累,教师要加强对学生读题能力和对题目整体把控力的培养,使其养成解题之前先研究图形特征的习惯.
3.教学中培养直观素养的必备性
此题巧妙融合了数形结合、转化、函数与方程、建模等基本思想,考查了学生对知识的理解能力,以及将未知问题转化成已知问题的迁移和应用能力,所有这些对思想与能力的考查,都自然地融合在层层推进的题意之中.直观想象是经历和经验的积累,以及逻辑链条的梳理.此题考查直观素养可以从这样两个角度来观察:首先,对于图形合理性的思考,图中除点A和点B是定点外,点P、点C和点D都是动点,点P可以视为“主动点”,点C、点D是“从动点”,这两个“从动点”的变化就引起了点E的变化,当点P在线段OB上运动时,一定存在射线AC和DB在第一象限的交点E.也就是说这个图形是合理的.其次,在平面直角坐标系内过点E作EH⊥Ox于点H是非常必要的,这样处理便于坐标的使用,也能很直观地发现△ACP∽△AEH,但是这个关系只能建立一个方程,而图中点P和点H的横坐标都是不确定的,所以还缺少一个等量关系.进一步探究,会发现△DPB∽△EHB可以提供这样一个方程,问题也就迎刃而解.

