数学概念的教学

张玉芳

摘  要：学生在学习数学概念时，受到生活经验以及旧有知识的影响，可能会产生认知偏差，这样的偏差在学术上被称为“迷思概念”，它不利于学生全面深刻地理解概念。文章中，笔者以“三角形的高”这一概念的教学为例，分析了学生可能存在的迷思概念及场生原因，并分享了笔者在教学中采取的纠正方法。

关键词：迷思概念;纠正;三角形的高;提质增效

一、前言

数学概念的教学，是整个数学教学中相当重要的一部分，其教学的核心在于帮助学生全面和正确地理解数学概念属性。概念的定义应该是概念名称与其相关属性的结合，教师的教学目标，就是要让学生能理解概念的相关属性并将概念名称与其属性对应起来。例如，我们在定义“三角形的高”这一概念时，就是如下展开的：“三角形的高是一条经过三角形某一顶点并垂直于该顶点相对边所在直线的线段。”在这一定义中，我们首先给出了概念的名称，即三角形的高，然后给出了其相关属性，即“线段”“经过三角形某一顶点”和“垂直于该顶点相对边”，这些相关属性给出了三角形高的全部特征，并使其区别于其他类似概念 [1]。这样的概念定义看似简单，但是概念的教学却没有那么容易，教师要做的不仅是让学生记住这些描述，更重要的，教师应帮助学生全面认识概念的内涵，帮助学生学会辨认，构建对应的认知结构，根据人的认知特点。我们在学习某一新概念时，总是倾向于先将它类比于先前的经验，学生在学习新概念时，往往会将其与先前学习过的知识或者生活中的经验混淆。有些时候，由于这些经验过于根深蒂固，学生甚至会对新概念产生错误的认知，这样的错误认知在学术上被称为“迷思概念”。学生在学习“三角形的高”这一概念之前，已经接触过了如平行四边形的高、梯形的高等类似的概念，那么这会对学生的认知产生哪些影响？会因此形成怎样的“迷思概念”？为了了解清楚这些情况，笔者对自己的学生进行了测试，先解释了什么是三角形的高，然后给出了不同的三角形，让学生尝试画出底边上的高。

二、对于“三角形的高”，学生存在的迷思概念以及原因分析

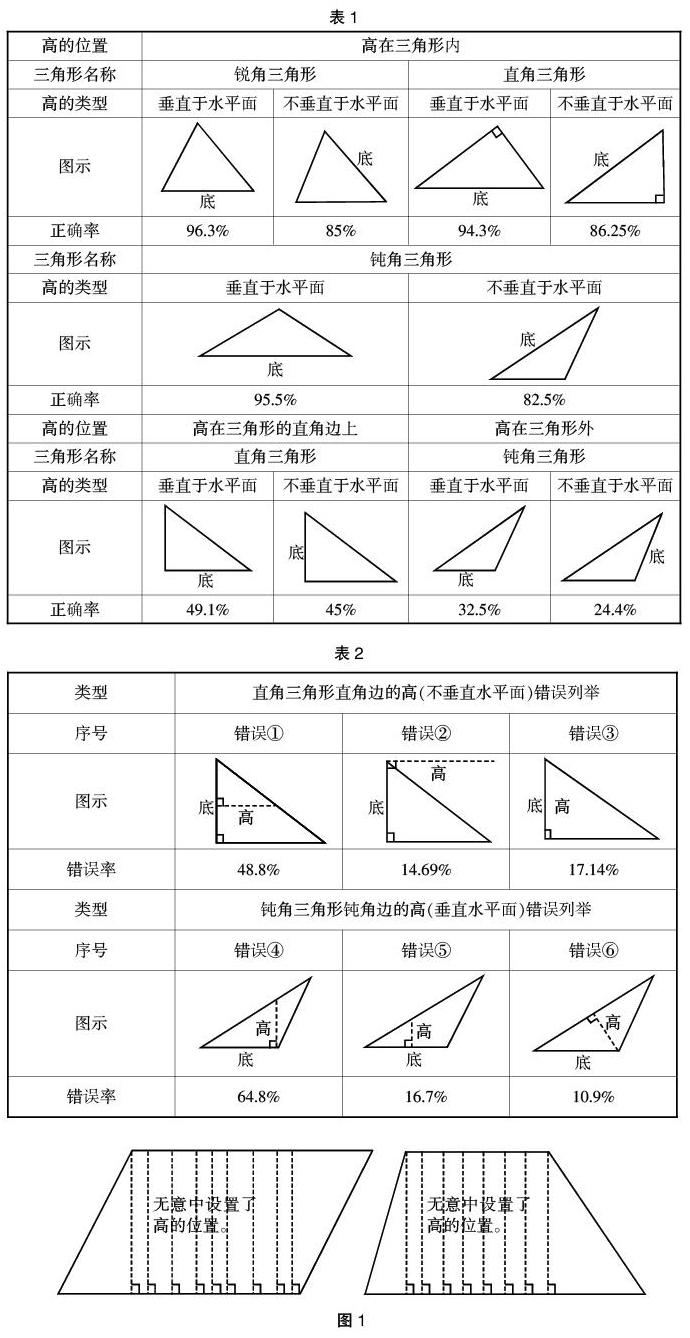
笔者对学生进行测试之后，得到了表1的结果。

在进行“三角形的高”这一内容的教学前，我们常认为其难点有二：其一是生活经验与数学概念的冲突，其二是钝角三角形高的辨认。生活中，学生对高这一概念的认知一般是“物体最高点到地面的竖直距离”，而在三角形的高这一概念中，参照面由地面转为了底边、对边，它们往往不平行于地面，具有一定的倾斜度，两者有较大的差别，学生学习起来可能有一定的难度。然而，通过分析结果表中的数据我们发现，对于同一个三角形，当其底边平行于地面或处于其他位置时，学生辨认的正确率差异为10%左右，并没有想象中那么大，究其原因，虽然生活经验与数学概念的差距较大，但是由于学生之前已经学习过诸如平行四边形的高等近似概念，他们对高在数学中的概念有了一定的认知，这降低了倾斜度这一影响因素的干扰力。而对于钝角三角形的高，由于存在钝角边上的高在三角形外这一特殊情况，一般来说小学教学中不做要求，但是，这样做会带来潜在的问题——由于缺少经验，学生们可能在学习过程中不自主地认为三角形的高就是在三角形内部的，这相当于在概念的定义中增加了一条有关位置的相关属性，从而局限了概念的定义范围。所以，虽然钝角三角形钝角边上的高在小学阶段不做要求，但是，为了让学生能够全面正确地认识“三角形的高”这一概念，教师应该要让学生接触这一特殊情况，并让部分比较优秀的学生尝试着去画一画这个在三角形外的高，帮助他们更加全面深刻地理解这一概念 [2]。

分析结果表格我们发现，学生在作直角三角形直角边上的高以及钝角三角形钝角边上的高时错误率较高，对比分析后，笔者认为，这主要是由于这两种情况下，高不在三角形的内部，与普遍情况不同。为了找出问题背后存在的迷思概念，笔者将学生的错误归类，希望从中找到问题的根源，具体情况如表2所示。

分析表2可以发现，学生犯“错误③”的主要原因是他们受到生活经验“高是垂直于水平面，是竖直的”这一迷思概念的误导。在其他情形下，学生都能理解“垂直于对边（底边）”这一属性，取一条垂直于底边的线段作为三角形的高，这时候错误产生的主要原因是学生忽略了高的第二条属性，没有让高经过三角形的某一顶点，分许学生的作图痕迹和笔记，对部分学生进行询问后，笔者发现了错误背后的迷思概念。

部分学生在作直角三角形直角边上的高时，从斜边上一点引了一条垂线到直角边上，并在旁边备注“边上任意一点”，结合学生的知识水平不难发现，他们将平行四边形的高与三角形的高混淆了起来。在作平行四边形的高时，是取边上任意一点向对边作垂线的，然而在作三角形的高时，“任意一点”变成了“某一顶点”，任意性变成了指向性，学生在学习时需要一定的适应过程。

那么为什么在作锐角三角形的高时，学生基本不会出错呢？笔者询问了部分学生，他们反映道，在画直角三角形直角边上的高或者钝角三角形钝角边上的高时，从顶点出发无法使得画出的线段在三角形内部，觉得“怪怪的”，转而选取了其他点，使高落在了三角形的内部。笔者认为，这是由于教师在讲解平行四边形或者梯形的高时，不经意间对高的位置进行了限定（如图1），学生在学习时误认为高应该在图形的内部，所以在产生冲突时很容易出现错误。

三、纠正迷思概念，构建正确的认知结构

经过测试和分析，笔者大概了解了学生在学习“三角形的高”这一概念时存在的迷思概念，为了降低其副作用，笔者采用了以下几个方法来尝试纠正迷思概念，帮助学生构建正确的认知结构。

1. 追根溯源，将前概念与新知识结合

数学知识具有一定的连贯性，学生学习的新知识往往和旧知识紧密相连，要想纠正迷思概念，第一步应该是追根溯源，发现前概念中与新知识中的相关部分，然后帮助学生从根源处理清概念内涵。三角形的高这一概念主要与“点到直线的距离”以及“平行四边形的高”有关，因此，笔者就从这两个前概念知识点出发，帮助学生正确构建认知结构。

具体的教学过程如下：

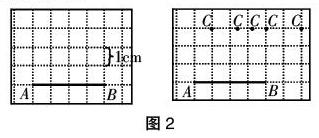
第一步，再现前概念场景。

如图2所示，格子图中每小格代表1cm，试问：与AB线段距离为3cm的C点在哪里？

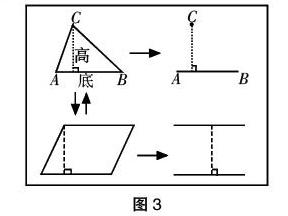
再通过这张图，让AB线段分别成为平行四边形、梯形的底边，引出高的概念，最后再以AB为底作三角形，让学生指出并解释什么是三角形的底和高，并让其明白，求某一图形的高最终可以转化为求某一点到某一线段的距离（如图3所示）。

2. 对症下药，利用认知冲突点进行概念构建

学生在三角形的高这一概念的主要认知冲突点就在高的位置上，教师可以抓住这一冲突，让学生直观地感受问题之所在，从而完整地架构认知。高相对于三角形的位置主要有三种：高在三角形内，高在三角形上以及高在三角形外，三种情况转换的节点就在直角三角形直角边上的高的位置上。笔者通过如下的动态演示，让学生直观感受到了高的位置变化，从最容易接受的锐角三角形的高到相对难接受的钝角三角形钝角边上的高，学生在演示过程中产生了认知冲突，通过情况对比，笔者对症下药，帮其解决了疑难之处。

参考文獻：

[1]  夏玉英. 结构化：一种必备的数学核心素养——结构化思维在小学数学教学中的应用及思考[J]. 数学学习与研究，2017（21）.

[2]  颜春红. 小学数学结构化教学课堂过程评价解析[J]. 现代中小学教育，2018（2）.