基于问题链的数学动态生成教学

孙丽娜

[摘  要] 問题是数学的心脏. “问题链”是教师根据教学内容，遵循严谨的逻辑结构设计出来的一组问题. 通过步步推进、逐层深化、相互关联的问题连接起来的问题链，引导学生对所学的知识主动探究，积极思考，合作交流. 在学生分析问题、解决问题的过程中，实现着学生个体能力的全面发展. 在这个过程中，学生有时也能发现教师预设之外的问题，这些问题引领学生去探索“美丽的风景 ”，促进数学课堂动态生成. 文章通过具体的教学活动，研究如何以问题链的形式来引导学生循序渐进、构建认知，发掘在教学中实施动态生成教学的有效策略.

[关键词] 问题链;动态生成

[?] 问题链与动态生成教学的意义及价值

随着国家教育机构当前对基础教育改革的不断推进，新的课改理念已逐步被世人熟知并不断地深入人心，新课程标准主要强调教育应该以人自身发展为本，并强调课堂教学不应该只是简单的“老师讲，学生听”这种单纯的知识传授过程，而应该是焕发着生命活力的一种师生共同成长的生命历程[1]. 动态生成式的教学模式不仅能够顺应当今新课改的需求，更拥有重要的现实意义. 动态生成式教学主要是指教师在授课中应该作为一个组织者、引导者和合作者，进而实现进一步改变传统的完全照搬式、机械僵化式的教学模式，再具体教学活动中应该以学生主动学习为主，适应教学情境的变化，创造性地利用已有教学资源和创造性学习资源，适时建构师生互动性强的、具有动态生成性的教学过程[2].

同时，由于中学数学的学习内容较为深奥难解，避免不了的会使教学过程趋于枯燥，如果数学教师过多的采用传统“灌输式”的教学方法，就很有可能会让学生失去学习数学的兴趣，致使课堂学习结果差强人意. 而通过问题链，数学教学不再是“琐碎问”“满堂灌”，而是以问题为导引，把学生看作教学活动的主体，重视学生主观能动性，让学生主动而有序、有向、有度地展开思考. 激发他们探索数学知识和数学规律的兴趣，以期实现数学教学过程中学生学习成果的优质化[3] .

[?]基于问题链的数学动态生成教学在数学课堂上的运用策略

1. 创设启发性问题链，引领动态生成

在课堂教学时，教师对于学生能够独立解决的问题应注重引导、启发，而不是强迫、代替. 可以设计“启发式”问题链，循循善诱，对学生启发诱导，引发学生的认知冲突使其能够大胆地去质疑和猜想，引领动态生成.

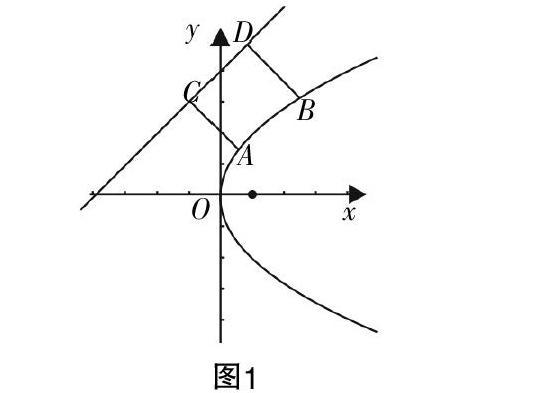
比如，讲述题目：如图1，已知抛物线方程为y2=4x，直线方程为y=x+4，一个正方形的顶点A，B落在抛物线上，顶点C，D落在直线上，求正方形的边长.

可设置如下的问题链：

（1）满足什么条件的图形是正方形呢？（为后面构造等量关系铺路搭桥）

（2）该怎样求正方形的边长？（通过观察、分析图像使学生明白应先求出顶点坐标的表示）

（3）该怎样构造等量关系建立方程组？（这是本题的关键，也是本题的重难点，应给学生留下充足的时间以小组谈论的形式让学生去思考、探究）

（4）如何求所选直线的方程？（抓住问题的关键，目的是求正方形的边长，因此所设的直线方程要和正方形的边长相联系）

（5）怎样通过建立的方程组求解出正方形的边长？（由弦长公式）

通过这一系列问题的设置，层层深入地启发学生思考，最终使学生通过自己的努力获得题目的答案，使学生体验整个探究的过程，享受探究的乐趣，并且通过对题目的解答也有效地锻炼了学生的思维，在掌握题目解答方法的基础上使学生的思维和智力得到了进一步的发展和提升[4].

2. 创设探究性问题链，创造动态生成

在教学方法的选择中，尽可能选择以培养学生探究思维和实践能力为主的动态生成性数学课堂，引导学生在学习中实现自主学习，发挥学生创新意识，实现对数学学习的再创造.

在实际课堂教学中，对于问题链的设计思路要清晰，并使所提出的问题尽可能面向全体学生，并为大部分学生所解. 紧紧围绕各章节乃至各教学要点为中心进行问题的设计和提问，做到所提出的问题知识点突出，贴近生活实际，适合多数学生的解题能力;让他们在解题中能够实现对知识的掌握和连贯式认知. 同时问题链的设计需要具有递进式的探究价值，使学生循序渐进地去探索、去感知. 在问题难度的设置上层层递进，激发学生探索欲，能够自主地去学习数学新知，获得更优化的问题式教学效果. 笔者认为，教师对于问题设计、提问方式、问题表达都要从学生实际出发，充分体现学生的主体地位，实现优质的动态教学生成.

比如，对如下题目的教学问题设计：已知函数y=lg（x2+mx+1）的值域为R，求 m的取值范围.

问题2：上述函数的值域都不是R，这是为什么？

问题3：要是函数y=lgx的值域是R，则自变量x要满足什么条件？

问题4：要使函数lgx2+a的值域是R，则字母a应该满足什么条件？

问题5：你能通过图像说明要使一个对数函数的值域是R，这个对数函数应该满足什么条件吗？

问题6：现在回到原来的题目：“已知函数lg（x2+mx+1）的值域为R，求m的取值范围. ”

上题通过一串循序渐进的探究式问题链，把一个较难的题目分解成几个联系密切、层次分明、梯次增加难度的题目，从特殊到一般，由易到难，一方面体现了数学知识发展的层次性，另一方面也满足了不同知识层次的需求，让学生根据自身的知识能力获得对新知的不同学习程度. 问题1入口较宽比较容易回答，大部分学生都能顺利完成，有助于激发学生的学习兴趣;问题2、问题3、问题4依次加深了难度，问题5反思提升，通过对前面问题的总结提炼，使学生认识到对数函数值域是R的实质;然后问题6返回题目本身，终使问题迎刃而解. 从不同的角度设置一串问题链，让不同知识程度的学生均有所思考，训练学生发散性思维的有效途径[5].

3. 创设批判性问题链，演绎动态生成

因为课堂教学存在着隐藏的不确定性和环境特殊性，致使任何课堂都无法提前演练教学中的所有设计，这就使得课堂教学应该最大限度地激发教师和学生彼此之间的互动和正向反馈. “动态生成性”这一概念摒弃了“预设性”课堂教学，教师在备课时需要想到所设计的问题，很有可能会得到学生多种不同的答案，这就要求教师能够在指导学生时批判性地看待学生的回答，能够根据具体教学情况和学生的思维模式，辩证性地分析问题，并巧妙地多设计多重答案的数学问题，让学生在回答问题时，能够碰撞出思想的火花，感悟多家之言，最终在自我反思和师生探讨中自行梳理出创造性、价值感强的答案.

该数学问题的回答过程列举如下：

学生1的回答：对于双曲线求渐近线的方程，可以“去了平方拿去1”，中间改成一个“+”“-”号. 反过来，根据渐近线的方程来求双曲线的方程，就可以把“拿去的1”放回去. 因此，可以把渐近线的方程更改为±=0，由于双曲线方程和渐近线方程的关系规律，所以双曲线的方程为-=1.

教师没有告知对错，而是转向其他同学，问道：同学们看看，这位同学的解题过程对不对？

一位学生举手回答说不对. 教师询问他的解题思路是什么.

学生2的回答：我认为第一位同学的解题过程是错误的. 假如把另一个条件M点的坐标代入该方程，就会很清楚地看到不符合要求，因此第一位同学的解题过程不正确.

教师赞许，说第二位同学的分析是有道理的. 然后进一步询问在座各位同学，有没有自己的解题思路. 学生2受到鼓励，信心大增. 同时其他同学也受到鼓舞，开始积极思考并自行讨论起来.

这时教师再继续问大家，学生1的解法有没有一定的数学道理？学生3站起来回答说是有道理的，但不清楚他具体错在什么地方.

教师这时需要审时度势，如果大部分学生确实不清楚出错的原因，就需要主动将问题进行剖析，以免耗尽学生的积极性. 教师回答：学生1的解题过程有一定程度的合理性，但结论却出现了问题. 大家跟我一起来想一想，双曲线方程为-=1，它的渐近线是±=0. 如果我们反过来看，渐近线方程是±=0，它的双曲线就一定是-=1吗？（学生们这时恍然大悟，开始思考出错点）

教师：好，请大家写出下列双曲线-=1，-=1，-=1的渐近线方程.

教师：大家一起来看这三个双曲线方程，有没有共同点或者相似处？

学生突然明白：老师给出的三个双曲线方程，他们的渐近线是一样的.

教师欣慰赞许：很好，那这个情况能够说明什么问题呢，刚刚那个题是不是这种情况？

学生恍然大悟：原来是这样，如果双曲线的渐近线方程是±=0，双曲线不一定就是-=1.

教师再进一步追问，引导学生做进一步思考：既然大家说这三个双曲线的渐近线是一样的，那么它们的方程之间有关系吗？

（学生开始了积极的探索…… ）

案例中，教师鼓励学生的同时，有助于有效调动学生的学习积极性. 首先当学生1出现错误时，并没有马上判定这位学生回答的对与否，而是让其他学生思考学生1的解题对不对，让学生自行批判，思考问题的合理与否. 在具体学习中，教师单单为引导学生，点拨思路，让学生尽可能地借助教师的引导，讨论、总结、反思解题过程的正确性和有无更合理的解决方法. 教师以问题链的形式通过层层设问，步步互动，努力用师生间、生生间的互动生成“再思考”突破变换的难点，不知不觉地推动课堂教学的动态生成. 让学生在不断实践中发现方法，解决问题，体会数学的思想与方法，感受自我习得数学知识的乐趣[6].

[?]结语

通过具体的教学實践得知问题链设计的原则与策略对提升教学质量、改善学生非智力因素是大有益处的. 一方面，问题链的设计对教师有较高的要求，这也迫使教师努力地去备教材、备学生、备自己，间接地提升了教师的专业水平和教学能力;另一方面，问题链式教学符合新教育背景下的教学要求，尊重学生的学习主体地位，它对学生数学知识的掌握、学习态度的改变、学习方式的转变、学习兴趣的提高等方面都有显著的效果，更是提高学生成绩的一种行之有效的方式. 动态生成的新颖数学课堂不仅要求教师有准确的判断能力和卓越的引导力，更需要教师善于遵照实际态势作出准确判断[7].

动态生成的课堂是课堂教学的最佳境界. 因为从本质上说，教学是一种“沟通”与“合作”的活动，教学的真实展开与推进是很难被规约与计划的. 用动态生成观来指导课堂教学，往往可能会使教学处于一个“无序”的混乱状态. 而基于问题链可以将课堂教学活动串联起来，使学生的注意力紧紧集中在课堂教学活动中，真正实现教学相长的目的.

参考文献：

[1]  林良富，范伟东. 动态生成：课堂教学新观念[J]. 浙江外国语学院学报，2002（6）：60-65.

[2]  李祎. 动态生成观下数学解题教学设计的改进[J]. 数学通报，2006， 45（5）：20-23.

[3]  赵玉玲. “问题链”教学法的探索与实践[J]. 现代教育，2012（z1）：88-89.

[4]  袁达煌. 如何正确运用启发式教学[J]. 读写算：教育教学研究， 2012（24）.

[5]  殷堰工. 试论问题链在数学教学中的作用[J]. 中学数学月刊，2008（10）：1-4.

[6]  吴祥忠. 高中数学课堂问题链的设计[J]. 数理化解题研究，2014（11）：34.

[7]  张素玲，吴维煊. 如何构建数学思维“问题链”[J]. 教学与管理， 2005（12）：63-64.