几何直观得结论 代数证明把理说

山东省邹平市第一中学

扈希峰 (邮编：256200)

山东省邹平市长山中学

王海燕 (邮编：256207)

函数性质的探讨是数学最重要的内容之一，在高考试题中，函数性质的分析不仅仅是重点，也经常作为整套题中的难点，往往安排在最后一题最后一问中.由于很多这样的题目表述比较抽象，所给出的参考答案也比较复杂，并设计一些技巧，使得很多学生望而生畏.如果在平时的教学过程中，注重培养观察能力，提高直观洞察力，这样的题目其实并非真的那么难.

几何直观是数学新课程标准里提出的十个核心概念之一，标准里提出几何直观主要是指利用图形描述和分析问题，借助它可把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.用最通俗的话说几何直观就是看图想事，看图说理.本文将具体分析几道“难题”，揭示几何直观观察对解答代数问题的启示作用.

例1(2007年高考全国卷(20))设函数f(x)=ex-e-x．

(Ⅰ)证明：f(x)的导数f′(x)≥2；

(Ⅱ)若对所有x≥0，都有f(x)≥ax，求a的取值范围．

(当且仅当x=0时，等号成立)

(Ⅱ)令g(x)=f(x)-ax，则g′(x)=f′(x)-a=ex+e-x-a，

(ⅰ)若a≤2，当x>0时，g′(x)=ex+e-x-a>2-a≥0，故g(x)在(0，+∞)上为增函数，所以x≥0时，g(x)≥g(0)，即f(x)≥ax．

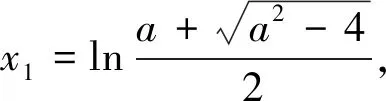
综上，满足条件的a的取值范围是(-∞，2]．

评注(1)从(Ⅱ)中“对所有x≥0都有f(x)≥ax恒成立”可以看到左边是指数型函数，右边是熟悉的一次函数，在x=0处的函数值相同，函数f(x)在x=0切线的斜率与y=ax的斜率相等，得到相切即临界位置的情况(如图1)，很容易得到参数讨论的临界值，再由几何意义得到参数取值范围，然后在每种情况下进行严格证明即可.此做法形象直观，讨论清晰，说理方便.

图1

(2)通过一些特殊点(端点值，零点值等)，寻求结论成立的必要条件，进而优化解题方法.该题(Ⅱ)中通过端点值a=f′(0)=2得到分类标准，进而在每种情况下进行研究即可.首先,我们要知道一个简单的结论：对于连续函数y=f(x),在x=x0处有f(x0)<0,则必定存在x0的一个邻域(x0,x0+ε),使得当x∈(x0,x0+ε)时，都有f(x)<0.

导数几何直观从“形”的角度，端点效应是从“数”的角度对该问题进行解释和求解.寻找解题的关键点，分类讨论的临界值，整体把握题目，思路清晰，顺利解答.

(Ⅰ)求f(x)的单调区间；(Ⅱ)如果对任何x≥0，都有f(x)≤ax，求a的取值范围．

解析(Ⅰ)

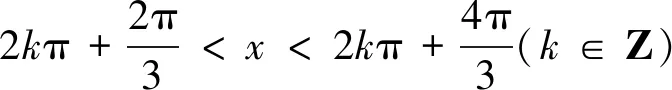
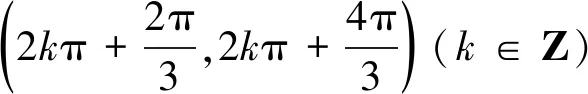
(Ⅱ)令g(x)=ax-f(x)，则

故当x∈[0，arccos3a)时，h′(x)>0．因此h(x)在[0，arccos3a)上单调增加．

图2

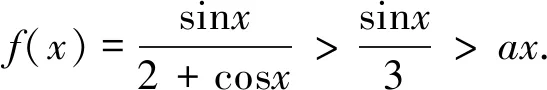
例3(2010年高考全国卷(21))函数f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的单调区间；(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围.

解析(Ⅰ)a=0时，f(x)=ex-1-x，f′(x)=ex-1.

当x∈(-∞,0)时，f′(x)<0；当x∈(0,+∞)时，f′(x)>0.

故f(x)在(-∞,0)单调减少，在(0,+∞)单调增加.

(Ⅱ)f′(x)=ex-1-2ax，由(Ⅰ)知ex≥1+x，当且仅当x=0时等号成立.故f′(x)≥x-2ax=(1-2a)x，

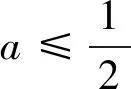
故当x∈(0,ln2a)时，f′(x)<0，而f(0)=0，于是当x∈(0,ln2a)时，f(x)<0.

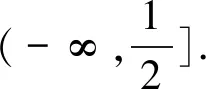
评注对于(Ⅱ)中“当x≥0时f(x)≥0”，易知f(0)=0，f′(0)=0，而f′′(0)=1-2a，采用端点效应，令f′′(0)=1-2a=0得到分类的标准，进而说理求解.

图3

证明已知0≤x≤1，显然有2x4≤2x成立.

评注如图3，通过图象可清楚的看到结论显然成立.该试题的命制注重了切线临界状态、端点效应方面的设计.探究试题的命题背景、命题方法，会有助于在解题中寻找入口、理顺思路、开阔视野，从而提高解题水平.

最后，在具体思考讨论有关函数的题目时，如果比较复杂，应该先画出函数图象的草图(或将题目条件等价变形后画出函数的图象)，对照题目的文字叙述，弄清楚题目条件、结论有什么直观意义(或几何解释)，题中的条件是否足以保证得到这样的结果或者关系.