基于CFD的超车过程车辆气动特性研究

唐洪涛，陈广厚，苗秀奇，董林源

(天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津科技大学机械工程学院，天津 300222)

近年来，随着社会的不断进步，汽车保有量快速增加，公路等级不断发展，路面状况越来越好，因此经常出现汽车高速超车的情况．对于不同等级的公路，其车道宽度不一，车辆行驶间距不一，行车速度有较大的差异，超车情况更为复杂．作用在汽车上的空气，35%～40%从车身上面经过，10%～15%流经汽车底部，25%被分离到汽车的侧面[1]，当一辆汽车超过另一辆车的时候，车身周围的空气流场和气压不断发生变化，它们之间将会产生强烈的气动干扰，这种干扰会对车辆产生附加力，引起车辆的阻力、侧向力和横摆力矩发生变化，对汽车的操纵稳定性和安全性有很大影响[2]．

目前，对超车过程的研究多是针对单一车辆的气动特性，或某一变量与两车气动力的关系，对超车时主超车与被超车所受侧向力变化规律与两车相对位置之间关系，以及车身尺寸对两车气动力影响的研究很少．大多采用的是稳态研究的方法，即用“有限递增步”[3]处理超车过程．但是，超车是一个瞬态过程，瞬态超车试验和数值模拟的结果更加接近真实的超车情况[4]．吴允柱等[4]在研究车速对超车车辆瞬态气动特性的影响后得出：被超车侧向力系数和横摆力矩系数的变化量随两车相对车速的增加呈线性增加的趋势．Minato等[5]利用激光流态显示方法对相同车型超车时车辆后面的尾流结构及其气动特性进行定性研究，表明超车过程中被超车会受到严重的影响．胡兴军等[6]在横向间距对超车气动特性影响的动态模拟中得出：侧向力系数在超车过程中变化最剧烈，变化幅度最大，对汽车行驶的稳定性影响最大．傅立敏等[2]在汽车超车过程的空气动力特性研究中指出：被超车的阻力、侧向力和横摆力矩都有最大值，且都在X/L为0～0.5范围内．车身尺寸对超车气动特性的影响，未见相关研究．

本文在上述研究的基础上，采用湍流动能二阶迎风格式、SIMPLE算法并结合动网格技术对超车过程进行数值模拟，得出相应的压力云图、速度矢量图、迹线图以及侧向力等数据，分析超车过程的侧向力变化规律与两车相对速度、超车间距、主超车长度与宽度之间的关系，以期为汽车设计和汽车驾驶提供参考，研究结果也可为交通安全系统的研究提供参考[7].

1 控制方程

1.1 连续方程(质量守恒方程)

任何流体流动问题都必须满足质量守恒定律．本文选用的汽车最大行驶速度为 108km/h，马赫数约为 0.0819，小于 0.3，因此可以认为此时气体是不可压缩的[7]．不可压缩流体的连续方程为

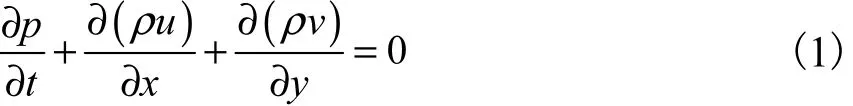
其物理意义是：对于不可压缩流体，气流微团在运动中，无论形状怎么变化，其体积总保持不变，即质量守恒．

1.2 运动方程(动量守恒方程)

在流场中取一个四边形微元体，假设其中心点坐标为(x，y)．在t时刻，流过此中心点气流微团的速度在 x、y方向的速度分量分别为 u、v，密度为 ρ，动力黏度系数为μ，作用在流体微元体上的压强为p．

x方向的动量守恒方程为

y方向的动量守恒方程为

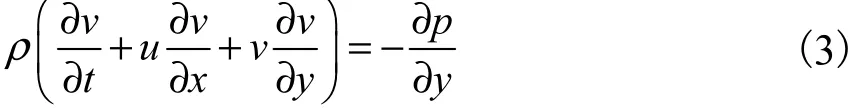
其中u、v、p可以通过式(1)—式(3)结合得出．

2 数值模拟

2.1 模型选取和计算域的设定

原始车型选用 Audi汽车某车型，其基本尺寸为：长 4886mm，宽 1810mm，高 1425mm．按长宽比例简化为平面矩形，长用L表示，宽用W表示．车头与车尾对照实车按比例做圆角处理．为保证超车时两车有足够的行驶距离，且不受两侧壁面的影响，所以设置计算域长度为30L，宽度为10W．

2.2 超车方案设计

两车均从右向左行驶，CarA为主超车，CarB为被超车；初始位置时，CarA 距离计算域右边界为 L，CarB超出CarA为2L；记CarA车头与CarB车头之间沿 x轴负向的距离为 X，用 X/L表示两车的位置．计算域和超车模型如图1所示．具体超车方案见表 1．

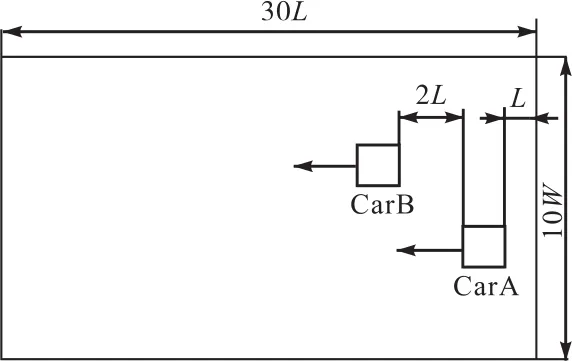
图1 计算域和超车模型Fig. 1 Computational area and overtaking model

表1 超车方案设计Tab. 1 Overtaking scheme

2.3 网格划分

模拟采用三角形非结构化网格，车身线网格步长设置为0.1，计算域网格步长设置为1．这样设置生成的面网格在车身附近较密，在保证了车身周围区域的计算精度的同时，也提高了计算效率．网格模型如图2所示．

图2 网格模型Fig. 2 Mesh model

2.4 边界条件和初始条件的设定

设置计算域入口和出口为压力入口和压力出口；两车车身为壁面；求解器型为非定常求解器；计算采用标准k-epsilon黏度模型，其余模型参数保持默认；湍流动能为二阶迎风格式，压力为标准大气压，勾选SIMPLE算法；动网格选择 Smoothing(网格光顺)和Remeshing(网格重划分)选项，设置弹性因子为0.05，最小网格尺寸为 0.04mm[8]，最大网格尺寸为1.2mm，最大网格斜度为 0.5，弹性因子即网格边界作用像弹簧或海绵一样，只能发生小变形的一个系数，网格不会增加或减少，大位移时需要网格重划分技术．网格重划分间隔设置为 1，即一个步长重新生成一次网格．设置的目的是更好地使局部网格重新划分，保障较好的网格质量．

3 模拟结果分析

3.1 超车压力云图分析

以工况 2的压力云图为例进行分析．分析时选取超车过程的 5个位置，分别为 X/L=-2、X/L=-1、X/L=0、X/L=1、X/L=2，结果见图 3．

在没有侧风的情况下，单车行驶车辆所受的气动力主要是阻力和气动升力，而侧向力和横摆力矩接近于零，复数车辆在超车时的受力则不同．

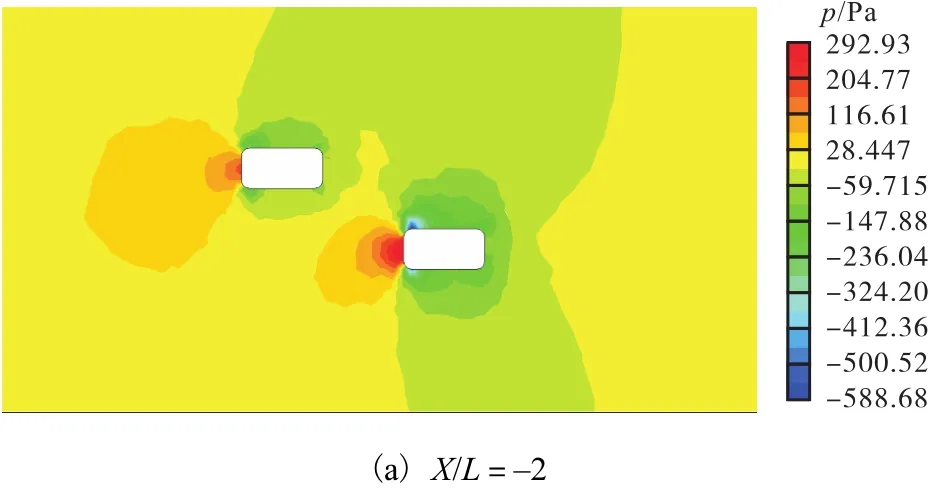
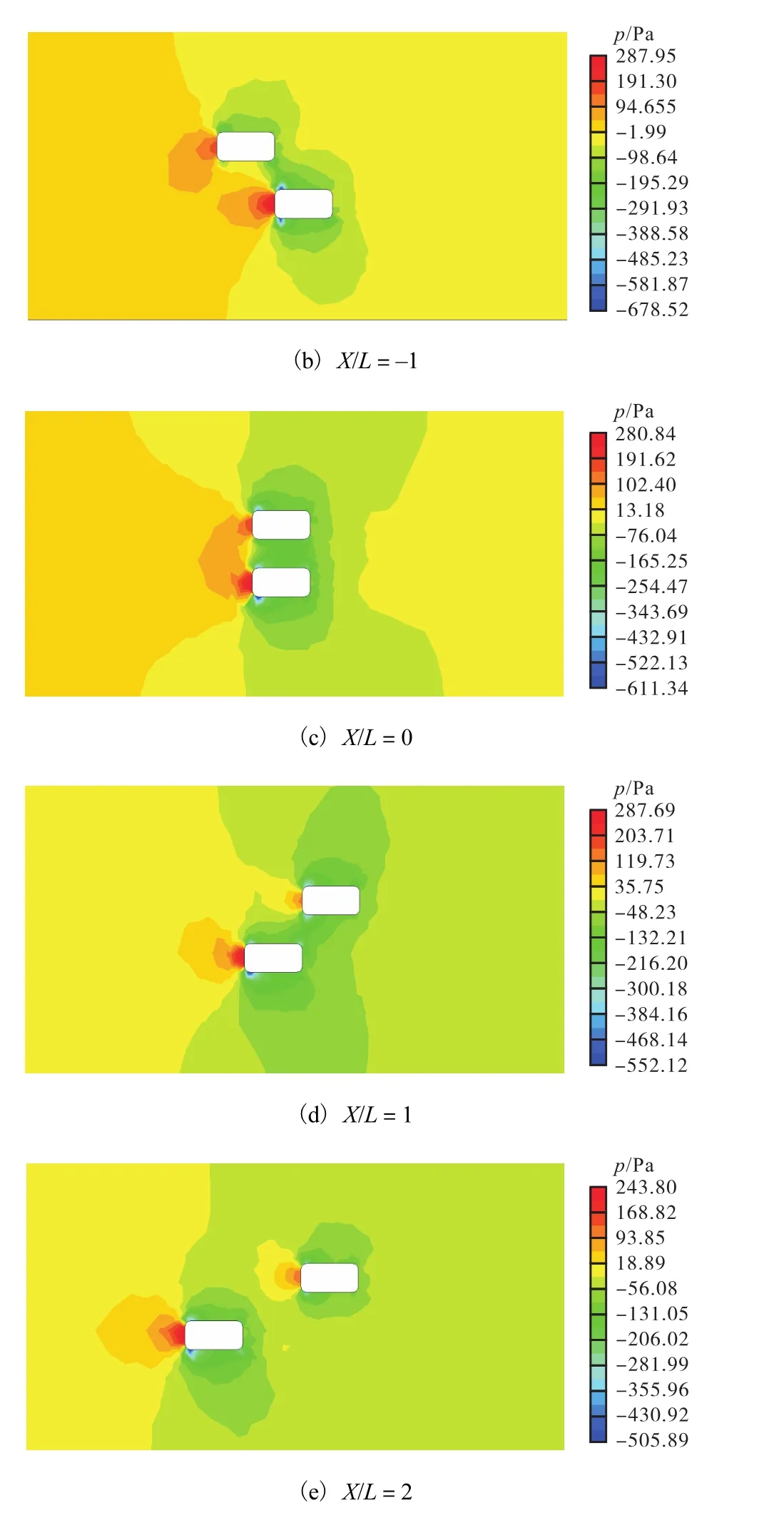
图3 超车压力云图Fig. 3 Pressure contours of overtaking process

如图3(a)所示，当CarA与CarB的距离为L，即X/L=-2时，CarA的高压区开始受到CarB周围压力的影响，CarA车头处正压区和CarB尾部正压区开始变得不对称，此时 CarA车头部位受到的偏离 CarB的侧向力逐渐增大．

如图 3(b)所示，当 CarA车头与 CarB车尾平齐，即 X/L=-1时，两车的正压区开始互相干涉，CarA的正压区对 CarB车身侧面产生压力，CarB车尾部的正压区逐渐消失，CarA车身整体受到一个向开阔区域转动的力矩，当车头受到的侧向力最大的时候，主超车的车头有向开阔一侧被推开的趋势，影响车辆的行驶稳定性．

如图3(c)所示，当CarA与CarB平齐，即X/L=0时，由于速度差异，CarB开阔侧与 CarA开阔侧的负压带不对称，两车车距较小，空气在两车之间急速流动，形成一个负压区，此时两车相互吸引，CarA侧向力也由之前的车头受到指向开阔一侧的力变为车身整体受到指向CarB的力．

如图 3(d)所示，当 CarA车尾与 CarB车头平齐，即 X/L=1时，CarB前方的正压区受到 CarA一侧气压的干扰，CarB的正压区逐渐缩小，此时 CarB的车头会受到一个指向 CarA方向的侧向力，CarA车尾受到一个指向 CarB的侧向力，这些力随着两车沿行驶方向的相对距离的增大而不断减小．

如图3(e)所示，当CarA超出CarB一个车身长度，即 X/L=2时，此时两车的压力场相互之间的干扰已经很小，随着 CarA继续往前移动，两车之间的干扰将越来越小，两车所受侧向力逐渐趋于零，恢复到单车行驶状态．

3.2 超车速度矢量图分析

从超车过程的速度矢量图可以看出，在运动的汽车周围存在一个运动的流场区域，运动的汽车带动周围的空气运动，流场的不断变化影响了气动力的变化．选取工况 1的速度矢量图进行进一步分析，结果见图4．

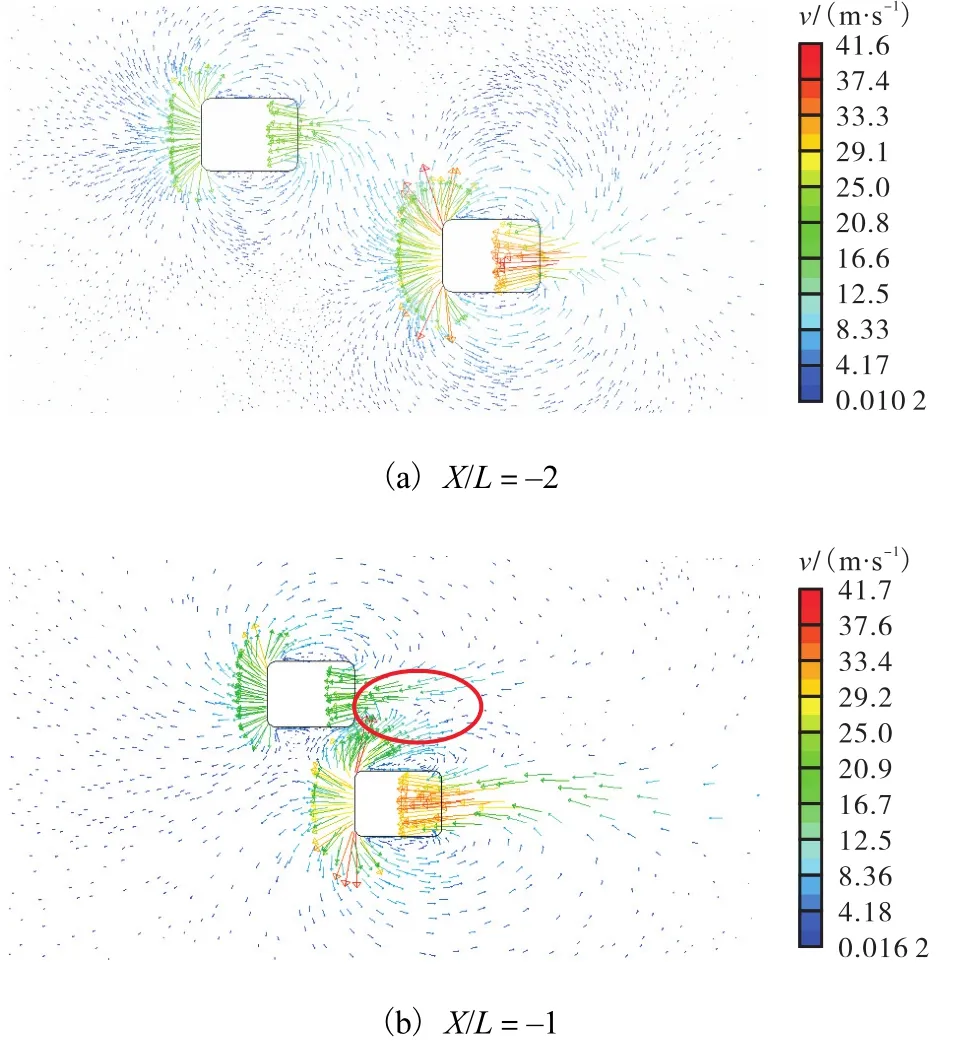
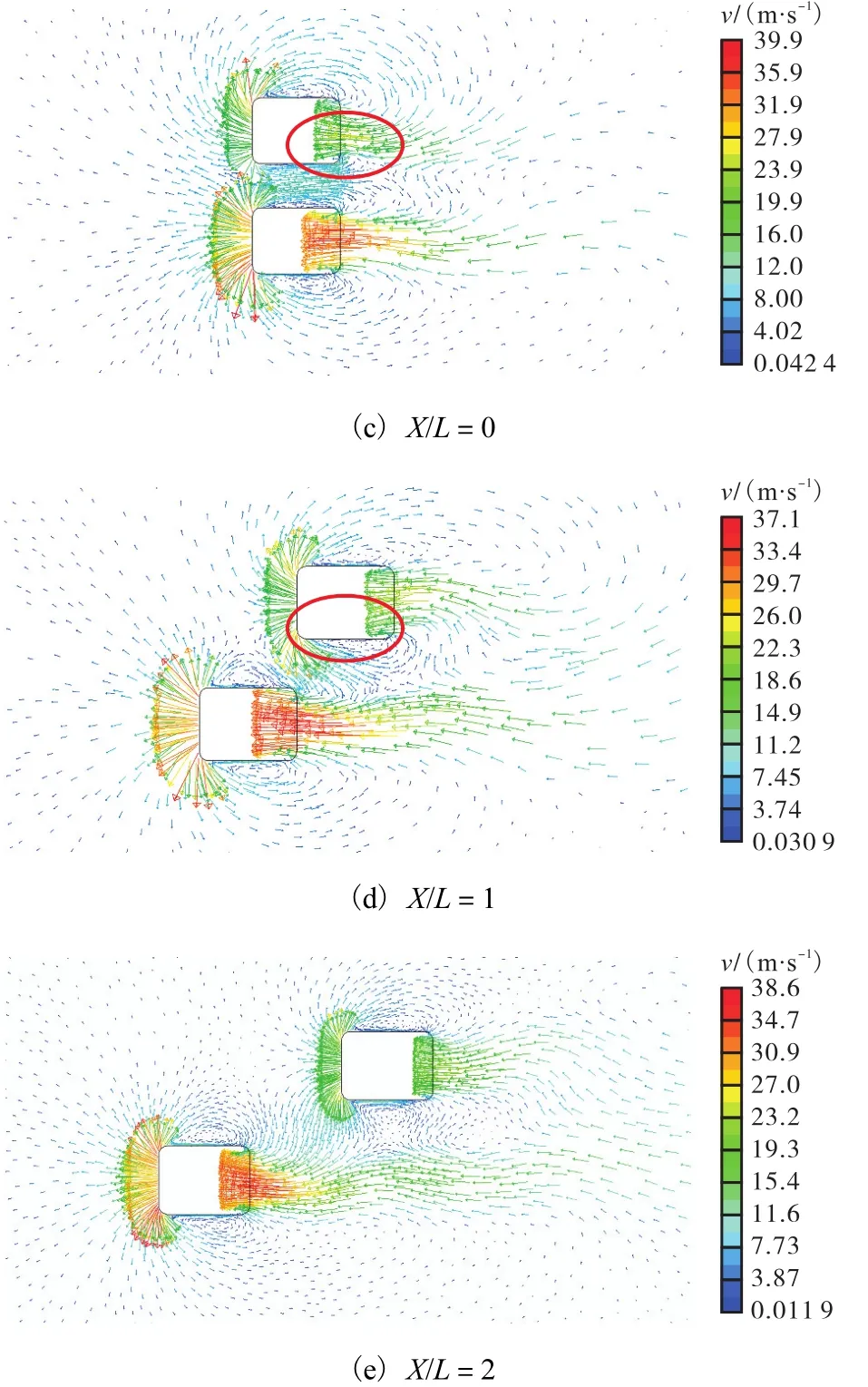
图4 超车速度矢量图Fig. 4 Velocity vectors of overtaking process

如图4(a)所示，当X/L=-2时，CarA与CarB的流场互相影响很小，两车各自的两侧近壁面处存在旋涡，且旋涡对称分布；随着 CarA 逐渐接近 CarB，两车的流场开始互相干涉，CarA前方的气流补充到CarB的车尾处，CarA车头受到一个指向开阔侧的侧向力，由于 CarA车头两侧的流场开始变得不对称，所以侧向力此时也不为零，随着距离的缩短，侧向力呈现增大的趋势．

如图4(b)所示，当X/L=-1时，两车的流场相互干扰非常强烈，CarA车头受到的侧向力很大；CarB车身干扰侧开始出现流动方向不同的旋涡，靠近CarA车头的一侧旋涡方向为顺时针，靠近CarB车头一侧的旋涡为逆时针方向，此时 CarB受到的侧向力也基本达到最大，方向指向开阔一侧．

如图 4(c)所示，当两车位置位于 X/L=-1至X/L=0之间时，CarB处于 CarA的负压带内，CarB的侧向力迅速减小，并在某一位置时变换方向，指向干扰侧，CarA所受侧向力也指向干扰测，此时两车之间的气流流速很大，根据伯努利方程得出，此处属于低压区[9]，两车为相互吸引的状态，CarB尾流对CarA所受侧向力的影响逐渐减小．

如图 4(d)所示，当两车位置位于从 X/L=0至X/L=1之间时，CarB车身干扰侧的负压区逐渐减小，CarB所受侧向力也逐渐减小，CarA车身干扰侧开始出现两个不同方向的旋涡，气流湍流非常激烈，CarA受到的侧向力在某一位置变换方向，指向开阔侧，侧向力也逐渐达到最大，方向指向开阔一侧．

如图4(e)所示，在两车的位置从X/L=1至X/L=2的变化过程中，两车间相对位置逐渐拉大，两车之间的气流干扰逐渐减小，相互作用逐渐消失，侧向力也随之减小，直至为0．

观察图 4(e)可以发现，CarA 的尾流轨迹很长，超过CarB之后还有一段时间会对CarB的车身外流场产生影响，并且轨迹有横向振荡的迹象，经过很长一段时间后两车的外流场才恢复到各自单车行驶时的流场状态．

3.3 侧向力数据分析

侧向力指车辆受到的垂直于汽车运动方向的力．汽车在超车过程中的相对位置不同，所受的侧向力也不同．当侧向力很大且急剧变化的时候，就会影响行驶稳定性，严重情况下还有可能发生事故．

3.3.1 不同超车速度时的数据分析

CarA 所受侧向力如图 5(a)所示，可以看出：侧向力变化曲线类似于正弦函数；相对超车速度越大，侧向力振荡越剧烈；在从X/L=0到X/L=1的变化过程中，侧向力转变方向．CarB所受侧向力如图5(b)所示，规律与CarA相似，不同之处为侧向力在X/L=-1至 X/L=0之间转变方向，且 CarB所受侧向力大于CarA所受侧向力．为了进行进一步分析，将超车过程中车辆受到的侧向力极大值与极小值的差定义为侧向力极值差．

图5 不同超车速度侧向力变化曲线Fig. 5 Varied overtaking velocity curve of side force

分析 CarB的 3侧向力极值差可得：在此位置时，工况2比在工况1的侧向力极值差增大17.1%；工况 3比工况 2的侧向力极值差增大 23%，工况 3比工况 1的侧向力极值差增大 44.1%．数据表明相对速度变化对被超车的影响大于主超车．

3.3.2 不同超车间距时的数据分析

超车间距不同时两车侧向力的变化曲线如图 6所示．

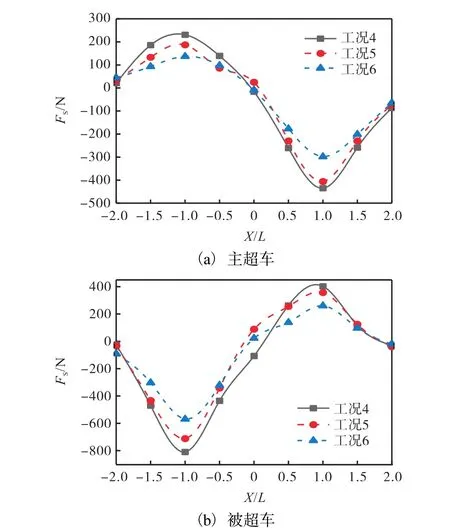
图6 不同超车间距时的侧向力变化曲线Fig. 6 Varied overtaking distance curve of side force

由此看出：超车间距变化时时，主超车与被超车所受侧向力的变化规律与相对超车速度变化时的侧向力变化规律相似．随着超车间距的增加，主超车侧向力震荡幅度减小，侧向力极值差减小．工况 5比工况4的侧向力极值差减小了36.3%，工况6比工况5的侧向力极值差减小了36.8%，工况4的超车间距是工况 6的 1/2，工况 4的侧向力极值差是工况 6的1.86倍．分析被超车的侧向力极值差得出：工况5比工况4的侧向力极值差减小28.8%，工况6比工况5的侧向力极值差减小了 8.1%，工况 4超车间距是工况 6的 1/2，工况 4侧向力极值差是工况 6的 1.39倍．改变超车间距，主超车受到的影响大于被超车.

侧向力变化规律类似正弦函数，在两车接近时先略有减少，然后增大至一个极大值，再减少至一个极小值，然后增加，基本上回到初始值[10]．

3.4 车身尺寸对超车影响

前文模拟结果表明在车距不变的条件下，被超车受到的影响大于主超车，所以改变主超车尺寸，被超车尺寸不变，研究车身尺寸对超车气动特性的影响．

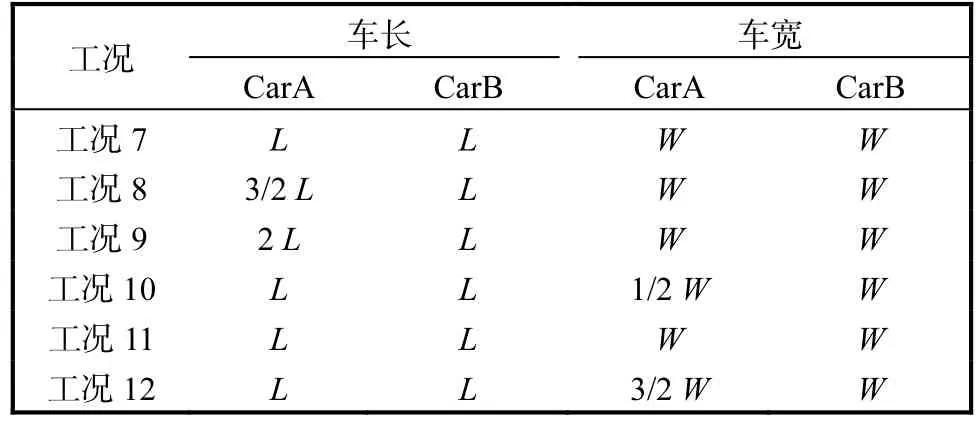
表2 车身尺寸设计Tab. 2 Dimensional design of car body

3.4.1 超车迹线图分析

选取工况7—工况12的X/L=-1位置的迹线图进行分析．迹线图设置为：着色方式下拉框中选择粒子变量，对不同编号粒子进行着色处理；释放粒子的平面选择车身边界与计算域入口和出口．从图 7中工况 7—工况 9在 X/L=-1位置的超车迹线图可以看出：随着主超车长度的增加，主超车两侧的漩涡尺寸不断增大，而且主超车干扰侧(指向被超车的一侧)漩涡与开放侧(指向计算域边缘的一侧)漩涡的尺寸差别也越来越大，这就造成主超车两侧受力不均，使主超车侧向力逐渐增大，横摆力矩也可能由此增大；被超车开放侧漩涡尺寸随着主超车长度的增加而加大，而干扰侧漩涡尺寸的差别几乎不变，这使被超车侧向力逐渐减小，横摆力矩也可能呈现减小趋势．

图7 工况7—工况9的超车迹线图(X/L=-1)Fig. 7 Case7-9 path of overtaking process(X/L=-1)

从图8中工况10—工况12在X/L=-1位置的超车迹线图可以看出：随着主超车宽度的增加，主超车两侧的漩涡尺寸越来越大，但是主超车干扰侧漩涡受到被超车干扰侧漩涡的挤压程度越来越小，相反随着主超车宽度的增加，被超车干扰侧漩涡越来越小，这就打破了被超车两侧涡的平衡，使得被超车侧向力逐渐增大．观察被超车尾流场也可看出，随着主超车宽度增加，被超车尾部流场受到主超车涡阻的强烈干扰，几乎将被超车尾流打断，造成尾流中涡的耗散．

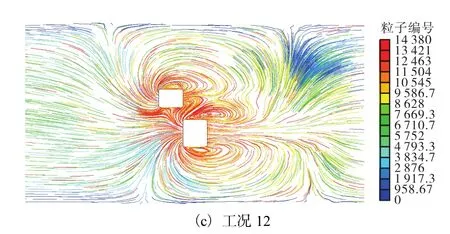
图8 工况10—工况12超车迹线图(X/L=-1)Fig. 8 Case 10-12 path of overtaking process(X/L=-1)

3.4.2 侧向力数据分析

由图 9可以看出，当主超车与被超车长度相等时，主超车侧向力变化曲线与正弦函数曲线相似；主超车长度增加，被超车长度不变时，主超车侧向力振幅加大，周期缩短，超车过程中侧向力变化方向的次数增多．当主超车长度分别为 3/2L、2L时，主超车侧向力极值差分别增大1%、17.4%，被超车侧向力极值差分别减小21.7%，37.1%．

图9 不同主超车长度时的侧向力变化曲线Fig. 9 Side force of varied length of main overtaking car

主超车长度变化时，对主超车和被超车侧向力极值差进行线性回归，得到图 10所示线性拟合直线．通过图10得出：随着主超车长度的增加，在超车过程中，主超车侧向力极值差呈增大趋势，被超车侧向力极值差呈减小趋势．主超车侧向力与主超车长度呈正相关，被超车侧向力与主超车长度呈负相关．

主超车宽度度变化时的侧向力极值差变化见图11．由图 11得出：主超车宽度增加，被超车宽度不变，主超车侧向力振幅减小，被超车侧向力振幅增大．当主超车宽度分别为1/2W、W、3/2W时，主超车侧向力极值差分别为 1440、1386、966N，呈现减小的趋势；被超车极值差分别为 1020、1723、2127N，呈现增大的趋势．

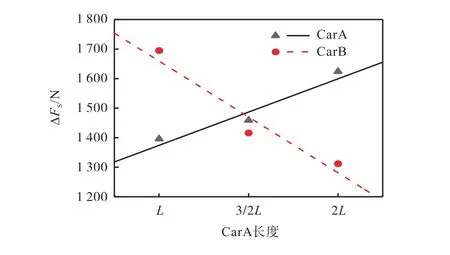
图10 主超车长度对侧向力极值差的影响Fig. 10 Influence of length of main overtaking car on maximum difference of side force

图11 不同主超车宽度时的侧向力变化曲线Fig. 11 Side force of varied width of main overtaking car

对主超车和被超车侧向力极值差进行线性回归，得到图12线性拟合直线，通过图12得出：在超车过程中，随着主超车宽度的增大，主超车侧向力极值差呈减小趋势，被超车侧向力极值差呈增大趋势．主超车侧向力与主超车宽度呈负相关，被超车与主超车宽度呈正相关．

图12 主超车宽度对侧向力极值差的影响Fig. 12 Influence of width of main overtaking car on maximum difference of side force

3.5 超速超车对被超车的影响

道路交通安全法规定高速公路最高限速为120km/h．现设定一组超速超车的模拟工况 13，主超车速度162km/h，即45m/s，被超车速度15m/s，车距2m，模拟结果如图 13所示．超速超车情况下主超车与被超车所受侧向力变化趋势与工况 1—工况 3的侧向力变化趋势相似，但是侧向力振幅明显增大，这使车辆的操纵稳定性有被破坏的趋势，对公共交通安全有潜在危害．

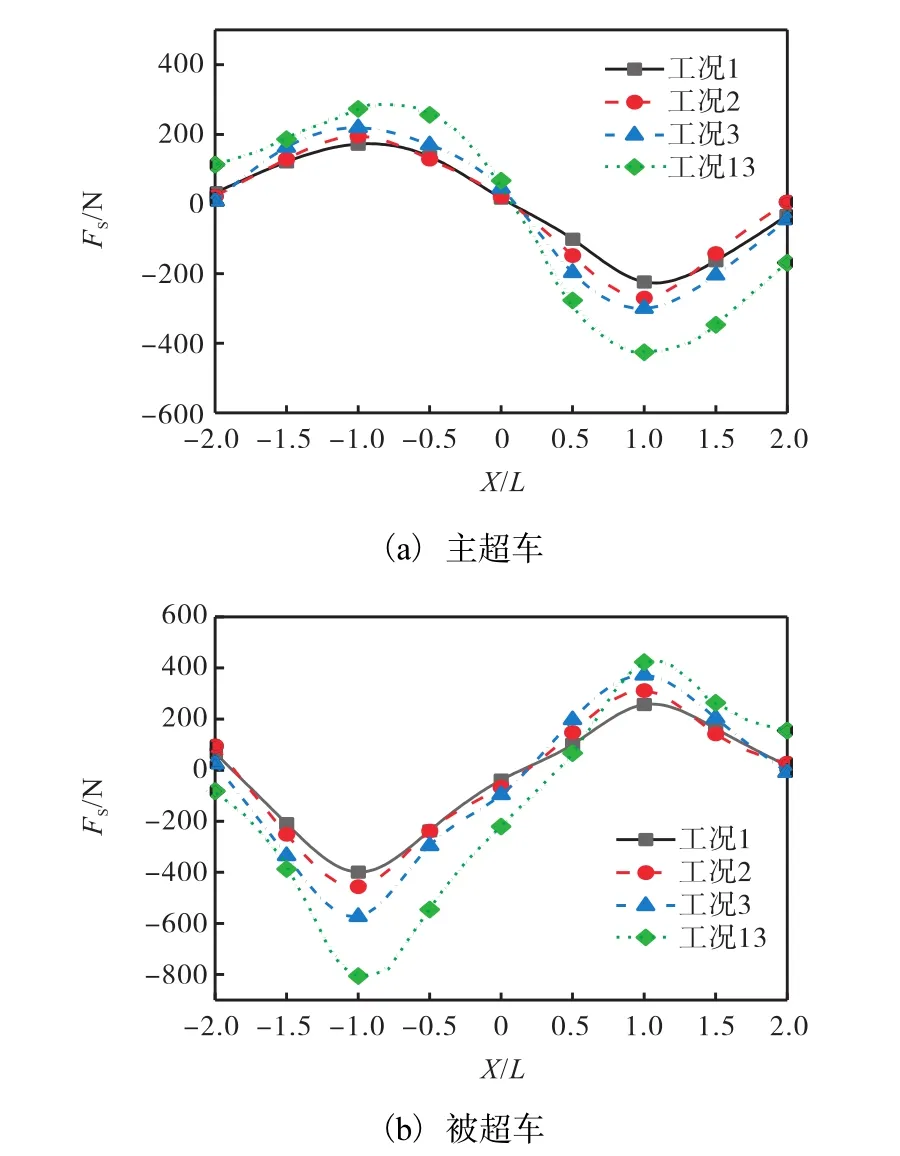
图13 超速超车时两车的侧向力变化曲线Fig. 13 Side force curve of both cars in overspeed overtaking

4 结 论

(1)相对超车速度增大，两车受到的侧向力变大；超车间距增加，两车受到的侧向力减小．

(2)主超车长度增加，主超车侧向力增大，被超车侧向力减小；主超车宽度增加，主超车侧向力减小，被超车侧向力增大．厂家在汽车设计阶段，设计合理的车长与车宽，能够降低车辆在复杂工况下的侧向力，提高气动稳定性．

(3)超速超车使两车所受侧向力变化更为剧烈，使车辆的操纵稳定性有被破坏的倾向，对公共交通安全有潜在危害．

(4)实际发生超车时，主超车超出被超车时主超车驾驶员要适当降速增距，以确保安全超车，这对于交通安全系统的发展有一定指导意义．