拉普拉斯矩阵在聚类中的应用

刘 颖，张艳邦

(咸阳师范学院数学与信息科学学院，咸阳 712000)

随着信息时代的发展，各行各业都产生了大量的数据，人们不再满足数据仅仅被电子化，而是希望对数据进行分析挖掘，透过数据的表象，找到隐藏在数据背后的规律和结构[1]．聚类分析是数据挖掘的一个重要工具，聚类分析的目的是从一个未知数据集中发现隐含在其间的数据内在结构信息，将数据划分为若干个不相交的子集，每个子集成为一个簇，同一个簇内数据相似性大，簇间数据相异性大[2]．数据聚类分析主要面临两个问题：一是如何确定聚类的结构；二是现在的数据大都是高维数据，如何能在聚类前对数据进行降维，从而提高聚类的效率[3]．这两个问题也是目前研究的热点．拉普拉斯矩阵(Laplacian matrix)也称为导纳矩阵，主要应用在图论中，作为一个图的矩阵表示，它广泛地应用在工程中[4-5]．聚类问题从图的角度看就是对图的分割问题[6]，因此拉普拉斯矩阵被应用到聚类分析中，出现了一种谱聚类算法(spectral clustering)，该算法的核心思想就是把样本空间的聚类问题转化为无向图G的图划分问题[7]．谱聚类算法在寻找聚类方面比传统算法(如k-means)更有效[8]．然而，当数据集很大时，谱聚类的时空复杂度都比较大．为了对大数据集进行聚类，基于拉普拉斯矩阵，结合样本点的密度和距离，介绍了一种新的候选聚类中心选择方法．该方法先利用拉普拉斯矩阵对数据集进行降维处理，对经过降维处理的数据求出其密度和距离两个参数，从而形成密度距离决策图；然后利用决策图选出候选聚类中心，对其进行合并，得到最终的聚类中心，最后将剩余点分配给聚类中心，完成聚类．实验结果表明了算法的有效性．

1 拉普拉斯矩阵

1.1 拉普拉斯矩阵的概念

拉普拉斯矩阵[9]主要应用在图论中，是表示图的一种矩阵．给定一个有n个顶点的无向图G=(V,E)，其中V表示所有顶点 v1, v2,…, vn的集合，E表示顶点之间连接的边的集合，拉普拉斯矩阵的定义如式(1)所示

式中：D 为图的度矩阵，W 为图的邻接矩阵．用图 1对拉普拉斯矩阵进行说明．

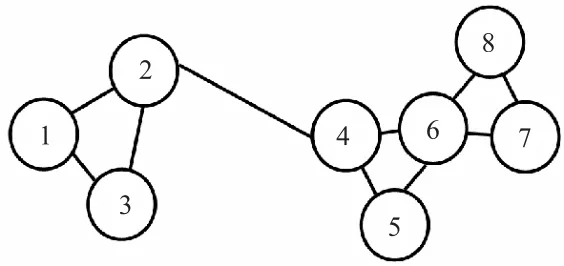
图1 简单无向图Fig. 1 Simple undirected graph

图1是由8个顶点组成的简单无向图，顶点的度简单的说是一个顶点连接的边的个数，度矩阵是一个对角矩阵，图1的度矩阵D为

根据式(2)可知，图1的邻接矩阵为

有了 D和W，根据式(1)可知，图 1的拉普拉斯矩阵为

1.2 拉普拉斯矩阵的性质

拉普拉斯矩阵具有以下4个性质[10]：

(1)拉普拉斯矩阵的最小特征值为 0，其所对应的特征向量为1．

(2)拉普拉斯矩阵是对称的半正定矩阵．

(4)对于任意向量f∈Rn有式(3)成立

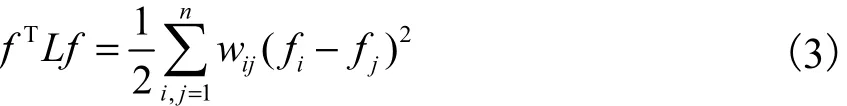
1.3 拉普拉斯矩阵特征映射

拉普拉斯特征映射(Laplacian Eigenmaps)[11]是从局部的角度出发来处理图，尽量在保留原图基本结构的情况下，将其映射到低维下表示．根据拉普拉斯矩阵的性质，得出拉普拉斯特征映射的基本思想是希望相互有关系的点如图1中的顶点1和顶点2，在降维后的空间中尽可能的靠近，相互之间没有关系的顶点如图1中的顶点1和顶点6，在降维后的空间中尽可能的远离．从拉普拉斯矩阵特征映射，发现其非常符合从高维数据中提取出能代表原始数据的低维表达这一情况．

2 拉普拉斯矩阵在降维中的应用

对于高维数据集来说，其包含有冗余信息以及噪声信息，使得这些数据在聚类的过程中准确率低，时空复杂度高．因此，为了高效发现数据的内在结构，通常在数据分析之前对数据进行降维处理，使用拉普拉斯的特征进行降维是目前流行的一种降维方法．

拉普拉斯特征映射的基本思想是对给定的有n个数据对象的高维数据集，在保持局部临近关系特征不变的情况下，找到数据集 A对应的低维数据集

降维的过程如下：

(1)根据K近邻求出数据集的邻接矩阵W，对任意一对数据对象xi和xj，若xi在xj的最近K个点内，则 wij=1，否则 wij=0；由于 xi与周围最近的 K个点之间的距离大小不一，为了精确刻画点之间的距离，根据数据的需要，还可以为每条边赋权，利用热核函数为每条边赋权W如式(4)所示．

(2)利用拉格朗日乘数法计算拉普拉斯矩阵L的特征值：

3 拉普拉斯矩阵在聚类分析中的应用

大多聚类算法都需要人为的选择聚类中心，经典的 k-means算法需在开始随机给出k个点作为初始聚类中心，经过不断迭代，最后选择稳定下来的聚类分布作为最后的结果，由于初始聚类中心的任意性，在很大程度上影响了聚类效果．2014年发表在Science上的一个聚类算法FSDP[12]，摒弃了 k-means随机选择聚类中心的不确定性．FSDP算法提出聚类中心一定是那些在某一个邻域内密度最高，且较其他高于自己密度的数据点的距离较远的点．算法构造一个横坐标为密度ρ、纵坐标为距离δ的决策图，供用户选择合适的聚类中心．其中：第 i个点的密度ρi表示在 i点的指定邻域 d c内包含的数据点的个数，即式(6)

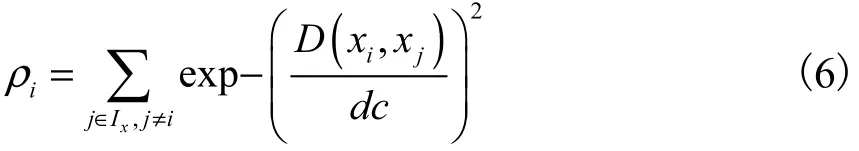
该算法对低维数据聚类分析有众多优点，以数据集flame为例，如图2所示．图2(a)为二维数据集的图形表示，图 2(b)为由密度ρ和距离δ组成的决策图，算法通过选择找到聚类中心(ρ和δ数值都大的点)．首先找到彩色的点即候选聚类中心，然后采用合并原则，对候选聚类中心进行合并，得到真正的聚类中心，最后完成聚类．

图2 Flame数据集及其决策图Fig. 2 Flame data set and its decision graph

由于此数据集维度低，且无噪声点，因此聚类效果好．对于维度高、噪声多的数据集，由于其特征冗余、噪声点影响，所以从决策图很难准确找到聚类中心，如图3所示．

对此类数据集的聚类分析过程如下：

(1)计算数据集 S = (sij)a×b的邻接矩阵M．

(2)计算数据集 S = (sij)a×b的度矩阵D．

(3)计算数据集 S = (sij)a×b的拉普拉斯矩阵L．

(4)利用拉格朗日乘数法计算拉普拉斯矩阵的各特征值和特征向量．

(5)对特征值按升序进行排序，自次小特征值起取 m个特征值，并求出其对应的 m个特征向量，这些特征向量组成新的矩阵．

(6)对新的矩阵按式(6)和式(7)分别计算ρ和δ，最后画出新的决策图，找到聚类中心，完成聚类．

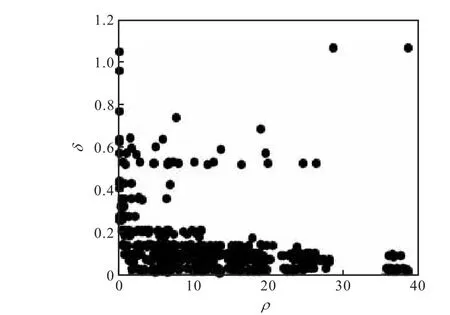
图3 高维含噪声数据集决策图Fig. 3 Decision diagram of high-dimensional noisecontaining data set

4 实验结果与分析

为了测试算法对不同样本数目、维度大小、类别数目的高维数据集的有效程度，特别从 UCI(http：//archive.ics.uci.edu/ml/datasets.html)中选出了 Dermatology、Credit approval、German credit、Wine、Ionosphere 5个数据集(维度大于10维、样本数目大小不一、类别数目不同)进行聚类分析实验，结果见表 1．

表1 高维数据集的聚类信息表Tab. 1 Clustering information table for high-dimensional data sets

为了测试算法在对高维数据有效的同时，不失去对低维数据的效力，特别从 Clustering datasets(http：//cs.uef.fi/sipu/datasets/)中选 出了 Flame、Jain、Smiles、Aggregation、Spiral 5个低维数据集(维度 2维、样本数目大小不一、类别数目不同)在同样的环境下进行了聚类实验分析测试，实验结果见表2．

表2 低维数据集的聚类信息表Tab. 2 Clustering information table for low-dimensional data sets

实验在个人电脑上运行，采用Matlab R2014b编程工具进行聚类分析．

以 Dermatology数据集为例对实验过程进行描述：

(1)设数据集 Dermatology为 S = (sij)a×b，a为样本数366，b为数据集的维数34．

(2)构造邻接矩阵 M =(mij)a×a，mij为样本 i与样本j的相似度．

(3)计算数据集 S = (sij)a×b的度矩阵 D =(dij)a×a．

(4)计 算 数 据 集 S = (sij)a×b的 拉 普 拉 斯 矩 阵L = (lij)a×b．

(5)利用拉格朗日乘数法计算拉普拉斯矩阵的各特征值和特征向量．

(6)对特征值按升序进行排序，自次小特征值起取 m个特征值，并求出其对应的 m个特征向量，这些特征向量组成新的矩阵 S'=(s'ij)a×m(m≤b)．

(7)对矩阵S'按公式(6)、(7)分别计算ρ和δ，最后画出新的决策图，找到聚类中心．

(8)将剩余的样本点按照最近邻原则分配到各个聚类中心，完成聚类．

表1的实验结果显示聚类数目选择正确，聚类效果良好，这表明通过使用拉普拉斯矩阵对数据集进行降维处理，能有效处理冗余数据和噪声数据，从而纯化数据集，提高候选聚类中心选择的正确率，进而达到了提高聚类效率和正确率的目的．表 2的实验结果表明，算法不仅对高维数据集有效，对低维数据集效力并没有消失，聚类数目选择正确，聚类结果正确率高，因此证明算法对聚类数据集一定的宽泛性．

5 结 语

本文讨论了拉普拉斯矩阵的原理，针对拉普拉斯矩阵的特征，首先，使用拉普拉斯矩阵对数据集进行降维处理，为数据的高效聚类打好基础；其次，结合FSDP算法，对降维后的数据集求出密度和距离，得到候选聚类中心，对候选聚类中心进行合并，获得最终的聚类中心；最后，将剩余样本点分配到各个聚类中心，求出最终的聚类结果．拉普拉斯矩阵的应用降低了冗余数据和噪声数据对数据结构的影响，在 10个不同样本数、不同维度、不同类别数的数据集上进行聚类分析实验，实验结果表明算法的有效性．拉普拉斯矩阵在聚类中的使用，凸显了拉普拉斯矩阵特征的实用性，为在其他领域使用提供了启示．