牛顿环实验真实暗纹级数的研究
张博涵
(石家庄第一中学 河北 石家庄 050031)
1 引言
牛顿环的等厚干涉实验是大学物理实验中最为广泛、最为普遍的一个实验.基本方法是通过读数显微镜对牛顿环的干涉条纹进行测量,进而计算出平凸镜的曲率半径.为了提高其曲率半径的测量精度,科研人员从各方面都进行了详细的研究.曹佳妍等人运用误差分析了测量暗环的最佳级数[1];徐少刚、谭亮等人探讨了软件在数值处理中的作用[2,3].周勇、宋淑珍等人重点分析了牛顿环中心圆斑大小对测量结果的影响[4,5].
在压力的作用下,平凸镜在接触面附近发生了不可避免的弹性形变,使得暗斑“吞噬”了若干条明暗圆环,因此,实验只能精确测出暗环的直径,却不能确定暗纹的真实级数.所以,既然暗斑不可避免,我们将注意力转移到如何能够确定暗环的真实级数,进而提高计算曲率半径的精度.同时,确定真实暗纹级数对于牛顿环在测量薄膜、玻璃弹性模量、液体折射率等方面具有积极意义.
2 原理与公式
牛顿环装置如图1(a)所示,平凸镜的曲率半径为R,离接触点O任一距离r处的空气薄膜厚度为e.考虑到光疏到光密的半波损失,故在薄膜上下表面反射的两束光的光程差为
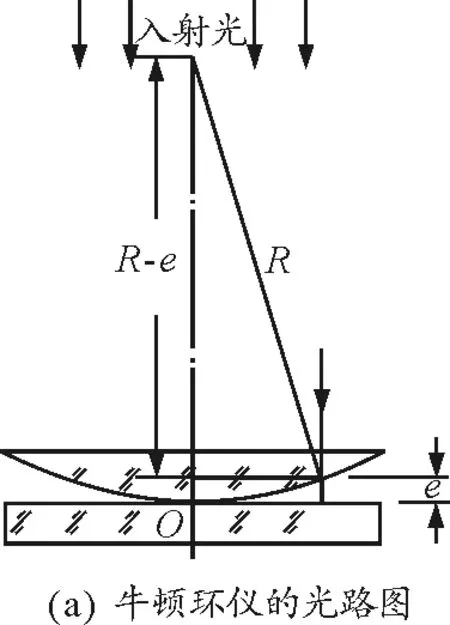

图1 牛顿环仪的光路图及干涉条纹
根据干涉条件,当光程差为半波长的奇数倍时,有
(1)
则干涉结果光强极小,形成暗纹.
由几何关系可知
R2=(R-e)2+r2=R2-2Re+e2+r2
(2)
略去二阶无穷小量e2,则得到任一暗环的半径为
(3)
特别指出,不忽略二阶无穷小量e2时,
(4)
本文将按式(4)计算.
3 数据处理与分析
对于牛顿环的暗环,我们测量了上百组数据(以暗斑偏大这一情况为例),设级数调整系数为m,数据处理分别采用以下3种方法.
(1) 逐差法:一般采用的方法是把测量的偶数个数据对半分成前后两组,后一组的数据与前一组的对应数据逐差再取平均.而对于此次测量数据,球面的曲率半径公式为
(5)

(6)
的形式,便可以拟合出曲率半径.
(3) 级数拟合:因为玻璃的弹性压力或者灰尘等影响,使得实际上的暗斑直径远比理论值大得多,因此,一级或二级,甚至三级的暗环都淹没于零级暗斑之中,拟合的结果就会相差很大.所以,在拟合的时候,我们重新考虑了每一条暗环的级数,将其作为未知量,设
k=m+nm=6
则
同时拟合可以得到n和R的数值.
以表1的实验数据为例,我们运用上述方法,采用R语言和1stOpt软件为工具[6,7],很好地解决了此问题.我们分别编写了R语言和1stOpt程序,计算了球面半径,并进行了对比(球面半径的真实值为2 000 mm).由表1可知,运用级数拟合的方法,可以更精确地得到曲率半径.
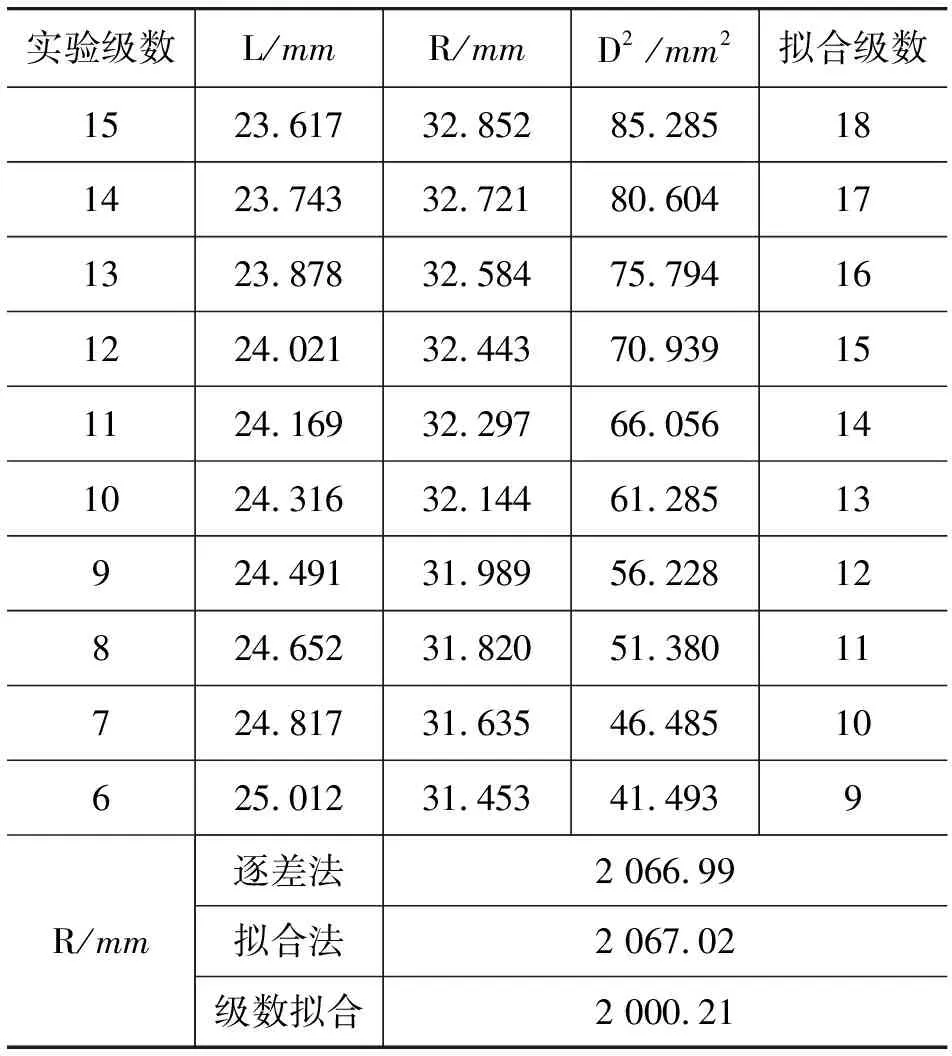
表1 实验数据及计算结果的对比
特别说明一下,从数据统计拟合的角度,由真实多次测量计算可知,采用R语言,运用统计分析的方法,可以得到更准确的曲率半径,并可以给出相关的Std.Error,t value,Pr(>|t|)值等信息.R语言计算结果如下:
Formula:x$D2 ~ f(R, lambda, m, n)
Parameters:
Estimate Std. Error t value Pr(>|t|)
R 2.067e+03 5.181e+00 399 <2e-16 ***
m 2.544e+00 3.348e-02 76 1e-12 ***
…
我们还可以调整牛顿环螺丝的松紧程度,并对牛顿环多次测量,以某3次测量为例,如表2所示.
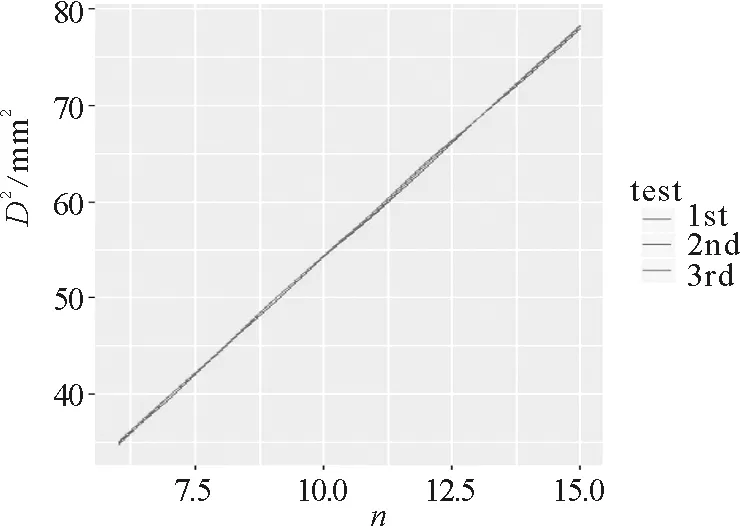
图2 暗环直径平方随n的变化曲线图
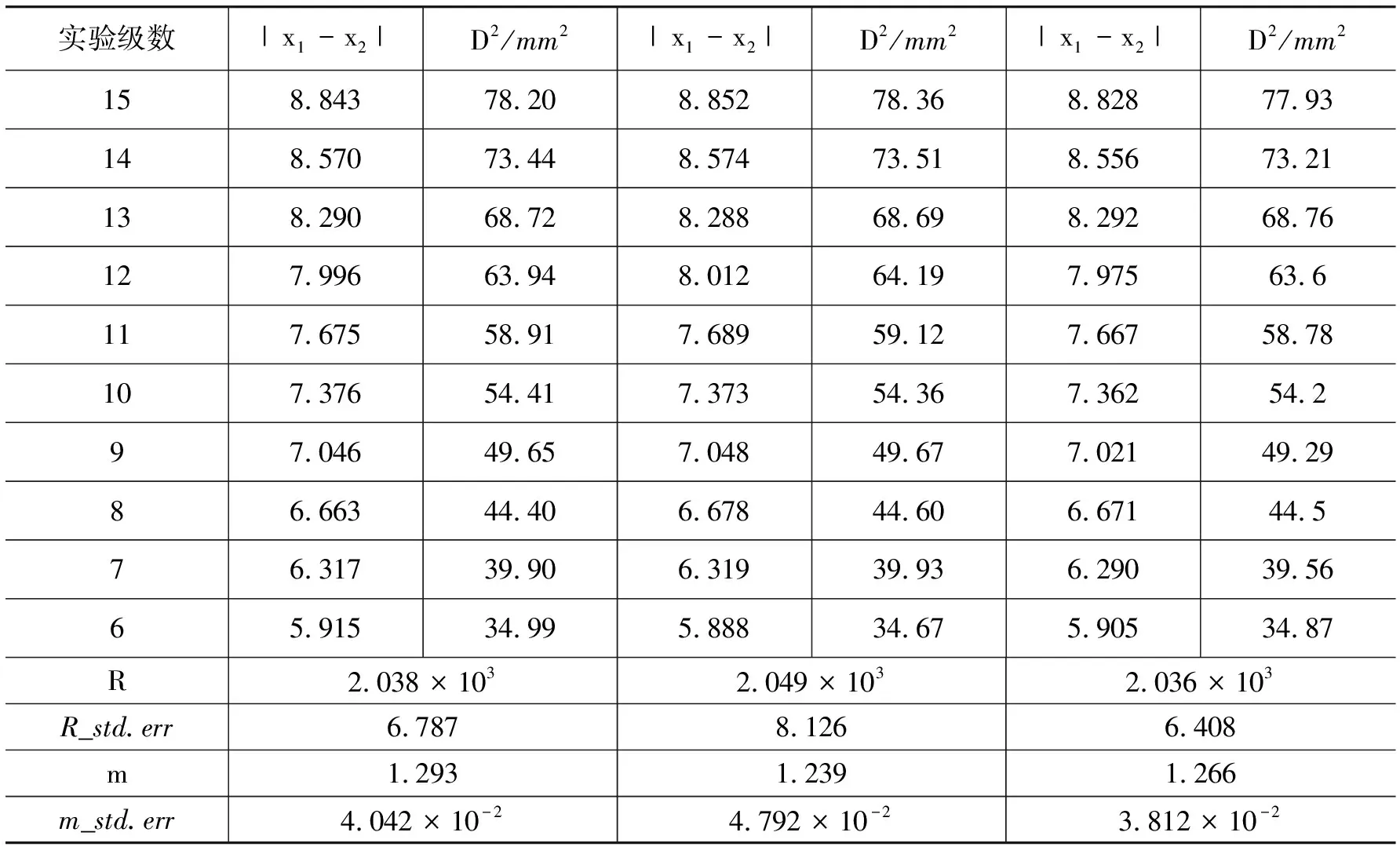
表2 牛顿环实验测量数据及计算结果
由图2,表2可以看出,在此特例中,测量结果具有很好的一致性和稳健性.R的平均值为2.041×103mm.级数调整系数m为2(取整后的结果).
4 反演验证
从表1还可以看出,同一个暗环,测量的和拟合的级数相差3个.测量的级数反而是错的?拟合的级数一定是准确的?为了说明这个问题,我们分析了暗环级数与直径的关系,如图3所示.可以看出,实验测量的直径变化曲线与理论曲线相差3个级数,而拟合的曲线与理论曲线符合得很好,这也说明我们拟合的级数是正确无误的.
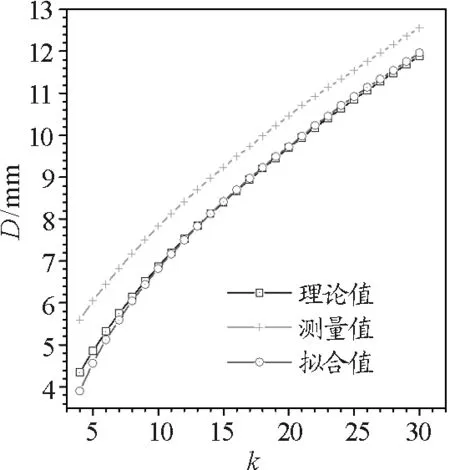
图3 暗环直径随级数的变化曲线图
5 结论
运用级数、半径同时拟合的方法,对实验数据进行数据处理,并与传统的数据处理方法做了对比.该方法不仅能精确得出平凸透镜的曲率半径,还能得出各个暗环的级数和暗环半径,是对该实验数据处理方法的一种创新.同时,真实暗纹级数的确定,对于牛顿环测量薄膜、玻璃弹性模量、液体折射率等具有很好的指导意义.
致谢:非常感谢河北地质大学物理实验中心杜国强、张江老师的指导,以及物理实验协会同学的帮助.

