试论线性代数学习障碍及解决策略

(山西广播电视大学，山西 太原 030027)

《线性代数》课程是国家开放大学(原中央广播电视大学)土木工程专业(本科)、水利水电专业(本科)统设必修课程《工程数学》的重要组成部分,在《工程数学》课程的终结性考核中占据相当重要的地位。由于数学课程具有高度的严谨性、抽象性的显著特点,是人们普遍公认的难学课程,掌握起来具有一定的难度。好多学生一听到数学两字就感到发怵,还没有进入学习就产生畏难情绪。所以在数学课程教学中,如何引导学生,克服畏难情绪,找到突破课程学习难点的金钥匙就显得尤为关键。那么破解《线性代数》课程学习的关键是什么?金钥匙又在哪里呢?

经过多年的教学实践,笔者认为,在教学中,如果教师能够充分利用初等行变换在课程中的作用，就是突破《线性代数》课程学习的关键所在。根据学习迁移理论,学习迁移是指一种学习对另一种学习的影响,或习得的经验对完成其他活动的影响。迁移广泛存在于各种知识、技能与社会规范的学习中。在线性代数的学习中,初等行变换是存在于学习始终的一种变换方法,在线性代数学习的始终都在发挥着重要而无可替代的作用。因此,教师若能够引导学生熟练地掌握初等行变换,能够正确地理解相关概念,就能够较好地完成本课程相关内容的学习。

在《线性代数》课程学习中,矩阵、方程组、矩阵的特征值及二次型是核心内容,在以上内容的学习中,逆矩阵的求法、矩阵的秩、高斯消元法解方程组及线性方程组的通解、向量组的极大无关组的确定、特征向量的确定都离不开初等行变换。而在行列式内容的学习中,我们常常用到的行列式的性质2、性质3、性质5与初等行变换有着异曲同工之处。所以熟练掌握初等行变换方法对《线性代数》课程的学习起着至关重要的作用。下面我们通过几个典型问题来谈谈初等行变换在矩阵及线性方程组学习中的具体应用。

一、求逆矩阵问题

问题1:已知X=AX+B,其中

求X。

分析:由矩阵减法运算先求得I-A,之后用初等行变换法求I-A的逆矩阵(I-A)-1,最后X的值为(I-A)-1B。

解:

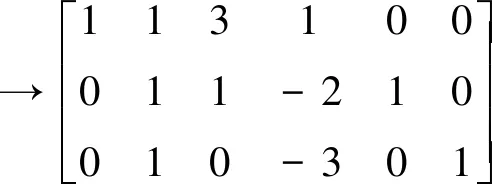
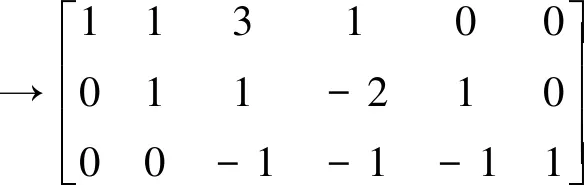
即

由矩阵乘法运算得

二、求矩阵秩的问题

问题2:求矩阵

的秩。

分析:首先对A进行运用初等行变换,使其化为阶梯形矩阵,则阶梯形矩阵的非零行的数目就是该矩阵的秩。

解:

所以,r(A)=2

三、高斯消元法解线性方程组

问题3:当λ取何值时,线性方程组

有解,在有解的情况下,求此方程组的一般解。

分析:首先对线性方程组的增广矩阵[A⋮B]进行初等行变换,化为阶梯形矩阵后,判断λ的取值情况,进而求出该方程组的一般解。

解:

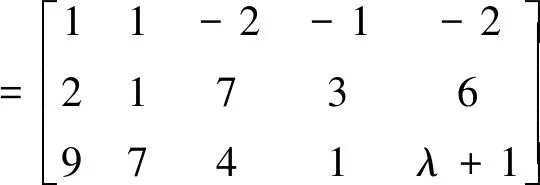
当r(A)=r([A⋮B])时方程组有解,所以当λ-1=0,即λ=1时此方程组有解。

此时方程组的一般解为:

(其中x3,x4为自由未知元)

四、线性方程组解的结构问题

问题4:求齐次线性方程组

的一个基础解系和通解。

分析:这是一个典型的齐次线性方程组求通解问题,我们只要按照齐次线性方程组求解方法,先将系数矩阵经初等行变换化为阶梯形矩阵,之后确定自由未知元,进而求出基础解系和通解。

解:

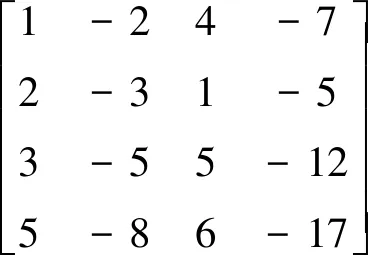
由此知x3,x4为自由未知元。

令x3=1,x4=0,得相应的解向量为

令x3=0,x4=1,得相应的解向量为

所以,{X1,X2}为方程组的基础解系。

该方程组的通解为:

X=k1X1+k2X2(其中k1,k2为任意常数)

问题5:设齐次线性方程组

μ为何值时,方程组有非零解?在有非零解时求其通解。

分析:本问题为齐次线性方程组求解问题。首先对所给定的齐次线性方程组判定何时有非零解。根据定理,当系数矩阵的秩小于方程组未知数个数时,齐次线性方程组有非零解。而现在的方程组,参数μ取值不同,方程组的解随之不同。当参数的取值满足系数矩阵的秩小于方程组未知数个数时,该方程组有非零解。

解:

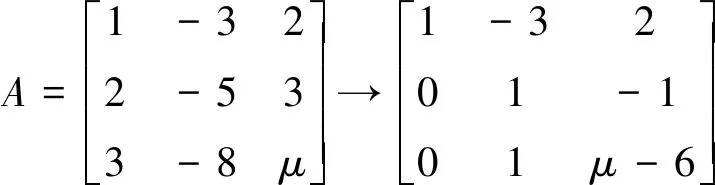
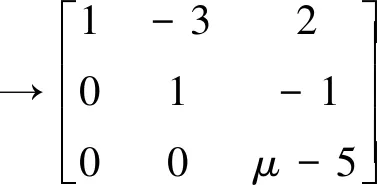
当μ-5=0,即μ=5时,方程组有非零解。

x3为自由未知元,令x3=1,得x2=1,x1=1所以该方程组的基础解系为

所以该方程组的通解为:

X=kX0(k为任意常数)

问题6:在线性方程组

中,

λ取何值时,此方程组有解?在有解的情况下求出通解。

分析:本题为非齐次线性方程组求解问题。首先对所给定的非齐次线性方程组判定何时有解。根据定理,当系数矩阵的秩等于增广矩阵的秩时,非齐次线性方程组有解。而现在的方程组,参数λ取值不同,方程组分为有解和无解两种情况。当参数的取值满足系数矩阵的秩等于增广矩阵的秩时,该方程组有解。我们还是先从初等行变换做起。

解:

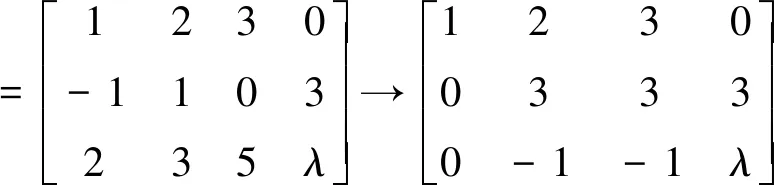
所以,当λ+1=0,即λ=-1时,r(A)=r([A⋮B])=2,此时方程组有解。

x3为自由未知元,令x3=0,求得x2=1,x1=-2

方程组的特解为:

不计最后一列,令x3=1,求得x2=-1,x1=-1

方程组的基础解系为:

所以该方程组的通解为:

X=kX1+X0(k为任意常数)

五、向量组极大无关组的确定

问题7:设向量组

求向量组的秩及其一个极大无关组。

分析:首先构造一个矩阵

用初等行变换把A化为阶梯形矩阵。则非零行的数目就是向量组的秩,主元所在列对应的原来向量组就是极大无关组。

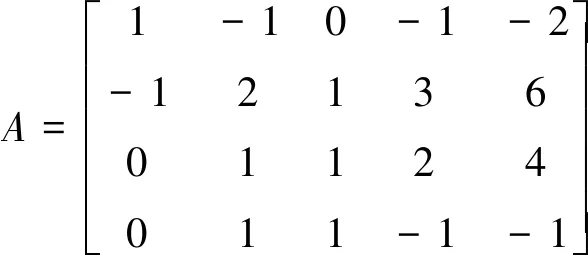
在教学中,学生主体作用发挥的程度取决于多种因素的影响,但起决定性作用的依然是教师。教师在教学中的引领作用发挥的好,学生的学习就可以少走弯路,比较好地掌握所学知识，否则学生的学习就会事倍功半。这就要求教师对教材有深入的研究,吃透教材,挖掘出教材当中对学生的学习起迁移引领作用的线索和知识点,促进学生学习的正迁移。