基于偏联系数的系统在临界点附近的变化趋势研究

(山西广播电视大学,山西 太原 030027)

20世纪60年代,经典集合论被发现存在漏洞,即所谓的集合悖论。为了解决集合论悖论,世界上众多数学家竞相开展研究工作。除严格规定集合存在条件，避免产生悖论的集合存在的公理化集合论[1]之外，典型的工作有美国学者扎德(L.A Zadeh)教授于1965年创立的模糊数学。模糊数学是描述和处理“亦此亦彼”的模糊不确定性的数学分支[2]。另外，我国学者赵克勤先生则在经过20多年对集合论中罗素悖论和哥德尔不完全性定理长期的潜心研究和思考，于1989年提出集对分析(Set Pair Analysis,简称SPA)理论。集对分析是把2个相互关联的集合组成集合对(简称集对),对集对中2个集合的确定性关系与不确定性关系及其相互联系进行研究，这不仅规避了集合论悖论,还把系统科学与数学从一个新的角度交融结合。集对分析的一个显著特点是,集对分析不仅仅靠计算得到的一个实数去说明问题,而是从“数的构成”去分析和寻找问题的根源[1，3],具有较为深刻的思想和方法论意义,能够利用集对分析中的联系数统一地研究、分析和处理由模糊、随机、灰色等多种不确定性所致的系统不确定性问题，集对分析也是一种用于处理和分析确定与不确定现象并存的不确定系统的不确定性决策分析方法。[3-11]其核心思想是把系统的确定性与不确定性作为一个不确定子系统来处理，对研究对象和研究过程中的不确定性客观承认，系统描述，定量刻画，具体分析的一种系统数学理论。

偏联系数是集对分析中的一个前沿概念。自赵克勤先生于2005年提出以来[5],已在飞机维修、地铁施工、火灾预防、区域创新、技术预警、教育评估、环境保护、管理决策、卫生统计、系统风险分析、矿山安全、水文水资源等领域得到广泛应用,发表了多篇重要的中文和SCI英文论文[6]，但目前还没看到研究三元联系数所刻画的系统在二阶全偏联系数为零时的临界点附近变化趋势的文献资料。2018年，受全国第6期偏联系数高级讲研班上赵克勤先生提出并完善的偏联系数理论的启示,本文研究三元联系数所刻画的系统在临界点附近的运动规律,揭示系统微观运动变化趋势,试图开创出关于三元联系数所刻画的系统与德国二战后在精神层面的反省和社会文化层面的转型相结合的综合研究新局面。

一、研究不确定性的系统分析方法

集对分析是研究和分析不确定性理论的一种新的系统分析方法[1]。联系数是赵克勤在集对分析理论中给出的一种结构函数，而偏联系数是联系数的一种伴随函数，它的计算过程刻画了联系分量在微观层次上的运动信息。

(一)集对的确定性与不确定性的三元代数描述

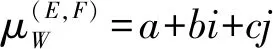
特别要说明的是,i为差异度的标记,是在a,b,c确定之后,为了说明差异度b的不确定性而设置的一个待定系数,由于i取值后把b分解,会导致a和c的增大或变小,因此,i在联系数中起着重要的作用。在广义集对分析中,i要在[j,1](0≤j≤1)内取值,j为对立关系数的标记,需根据不同的对立类型取值。

另外，在联系数μ=a+bi+cj中,i和j有双重含义:

一重含义是i和j分别作为差异度b和对立度c的系数。我们规定:i在[-1,1]区间视不同情况取值;j在一般情况下规定其取值-1,以表示对立度c与同一度a有负与正相反的属性。

另一重含义是不计较i和j的取值情况。此时只起标记的作用，即表示b是差异度,c是对立度,并以这两个标记与同一度相区别。

例如,一所学校有200位教师,现在以投票的方式选拔其中一名为某部门领导,如果有100人投赞同票,60人投反对票,另外40人投弃权票,这时的投票结果就可以用联系数写成μ=100/200+40/200i+60/200j或写成小数式μ=0.5+0.2i+0.3j。

(二)三元联系数的伴随函数——偏联系数作用

一个联系数有多个伴随函数,常见的有偏联系数、邻联系数、态势函数、势函数等。

偏联系数揭示出一个联系数所刻画的系统蕴藏着的某种潜在发展趋势。一个三元联系数的偏联系数又分为一阶偏正联系数、二阶偏正联系数、一阶偏负联系数、二阶偏负联系数、一阶全偏联系数、二阶全偏联系数。

定义1,记三元联系数μ=a+bi+cj的一阶偏正联系数为∂+μ,则

(1)

其中∂+a=a/(a+b)表示当前状态a原本处在b层次上,是从b层次正向发展而来;∂+b=b/(b+c)表示当前状态b原来处在c层次上,是从c层次正向发展而来。

此时，一阶偏正联系数∂+μ还带有不确定系数i。

定义2,记三元联系数μ=a+bi+cj的二阶偏正联系数为∂2+μ,则

∂2+μ=∂+(∂+a+∂+bi)=

(2)

可以看出，二阶偏正联系数∂2+是一个不带不确定系数的值。

定义3,记三元联系数μ=a+bi+cj的一阶偏负联系数为∂-μ,则

(3)

其中∂-b=b/(a+b)表示当前状态b原本处在a层次上,是从a层次负向发展而来;∂-b=c/(b+c)表示当前状态c原来处在b层次上,是从b层次负向发展而来。

从(3)式可以看出，此时一阶偏负联系数∂-μ还带有不确定系数i,j。

定义4,记三元联系数μ=a+bi+cj的二阶偏负联系数为∂2-μ,则

∂2-μ=∂-(∂-bi+∂-cj)=

(4)

从(4)式可知，此时二阶偏负联系数∂2-μ只带有不确定系j，而j=-1,即时此∂2-μ为确定值。

定义5,记三元联系数μ=a+bi+cj的一阶全偏联系数为∂±μ,二阶全偏联系数为∂2±μ,则由(1)、(3)式得

∂±μ=∂+μ+∂-μ

(5)

由(2)、(4)式得

∂2±μ=∂2+μ+∂2-μ=

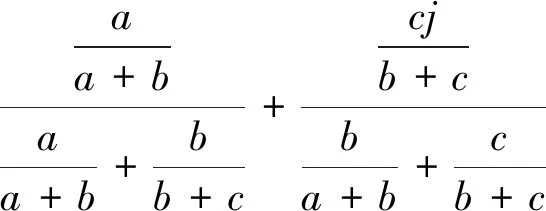
(6)

从式(5)可以看出,三元联系数的一阶全偏联系数仍是一个三元联系数,即含有不确定的因素;从式(6)所表示的二阶全偏联系数可以看出,j在取-1的情况下二阶全偏联系数是一个定值，此时可以对二阶全偏联系数作适当的分析。当∂2±μ>0时,表示三元联系数μ所刻画的事物发展趋势是正向发展趋势;当∂2±μ<0时,表示三元联系数μ所刻画的事物发展趋势是负向发展趋势;当∂2±μ=0时,表示三元联系数μ所刻画的事物发展趋势恰好临界。

一般情况下，对n元联系数的(n-1)阶全偏联系数也可做类似的分析。

(三) 打破临界点附近的平衡需作人为干预

如何从静态信息下挖掘动态信息,使系统或事物向我们期待的方向发展,是偏联系数的奥妙所在。

定义6,三元联系数的二阶全偏联系数∂2±μ为零时,我们称三元联系数所刻画的系统处于临界状态,此时称(a,b,c)为三元联系数的临界点,简称系统临界点或临界点。

定义7，对于三元联系数μ=a+bi+cj来说,当b=0,a=c时,代入式(6)得∂2±μ=0,此时表示三元联系数所刻画的系统处于确定的平衡状态,简称第一平衡态;当b≠0,a=c时,代入式(6)得∂2±μ=0,此时表示三元联系数所刻画的系统处于蕴含着不确定性的平衡状态,简称第二平衡态;当a≫b,c≫b,b≠0,即,a,c远远大于b(b≠0),且a,c接近或位于同一个十分位小数区间内,此时也可以说系统处于第二平衡态的逼近状态,换句话说，∂2±μ在临界点附近,这时事物发展趋势较为复杂。

由于联系数所描述的系统数据是动态的，如果希望事物向正方向发展或向负方向发展,需有外界因素干预该事物,也就是要考虑该系统所在环境对该系统所起的作用。

二、偏联系数分析结果与德国二战历史惊人一致

本文数据来自2014年2月20日《中国教育报》:德国前总理威利·勃兰特于1970年12月7日在华沙犹太人隔离区反法西斯起义纪念碑前下跪,此举在德国国内屡遭非议。据德国《明镜周刊》即时民意调查显示,48%的联邦德国公民视此举离谱,41%表示认可,11%不作表态。有关媒体称该事件为“惊世一跪”,现用前述的偏联系数知识分析如下。

(一)事件的偏联系数分析结果弱正向发展

用三元联系数描述刻画德国前总理的惊世一跪,此事件的同异反(同-认可;异-不作表态;反-视此举离谱)联系数为μ=0.41+0.11i+0.48j。

现取联邦德国公民对德国前总理的惊世一跪表示“认可”和“不作表态”两种情况作为研究对象。由于“认可”的比例是0.41,“不作表态”的比例是0.11,所以有同异型联系数μ(认可，不作表态)=0.41+0.11i。该同异型联系数的偏正联系数∂a=a/(a+b)=0.41/(0.41+0.11)=0.788,偏负联系数∂b=b/(b+a)=0.11/(0.11+0.41)=0.212,所以得全偏联系数∂μ=∂a+i∂b=0.788+0.212i。虽然i在[-1,1]区间取什么值要做具体分析,但这里可以从“最不理想”的情况考虑，此时i=-1,这时∂μ=0.788-0.212=0.576,因 0.56>0,所以认为联邦德国公民对德国前总理的惊世一跪随着时间的推移大家是认可的,总的发展趋势是向好的方向发展。

同理,可以取对这一事件“认可”和“认为离谱”两部分人作为研究对象。由于“认可”的比例是0.41,“认为离谱”的比例是0.48,所以有同反型联系数μ(认可，认为离谱)=0.41+0.48j。该同反型联系数的偏正联系数∂a=a/(a+c)=0.41/(0.41+0.48)=0.461,偏负联系数∂c=c/(a+c)=0.48/(0.41+0.48)=0.539,所以得全偏联系数∂μ=∂a+j∂c=0.461+0.539j,当j=-1时∂μ=0.461-0.539=-0.078,因-0.078<0,所以此时联邦德国公民对德国前总理的惊世一跪是微弱地向认为离谱的方向发展。

同理,可以取对这一事件“不作表态”和“认为离谱”两部分人作为研究对象。因“不作表态”的比例是0.11,“认为离谱”的比例是0.48,所以有异反型联系数μ(不作表态，认为离谱)=0.11i+0.48j。该异反型联系数的偏正联系数为∂b=b/(b+c)=0.11/(0.11+0.48)=0.186,偏负联系数∂c=c/(b+c)=0.48/(0.11+0.48)=0.814所以得全偏联系数∂μ=0.186i+0.814j。当考虑最不理想情况时,取i=-1,j=-1,所以最不理想时的全偏联系数值=-0.186-0.814=-0.99,因-0.99<0,说明这两部分人在最不理想情况下,存在向离谱的方向发展。这里也说明了此举在国内屡遭非议的原因所在。

综合以上三个方面的分析可以看出,进一步的发展趋势存在一定程度的不确定性,事实上,这种不确定性的程度在联系数μ=0.41+0.11i+0.48j中已经表明至少是11%。进一步的分析还可以认为在0.41中也有0.41*0.11=0.0451的不确定性;同理,在0.48中也有0.48*0.11=0.0528的不确定性;特别是0.41与0.48位于同一个十分位小数区间[0.4,0.5]中，……如此等等,都说明当时德国民众对前总理惊世一跪的认识发展,不仅取决于当时的认识,还取决于认识环境的日后变化。

另外一种分析方法,用二阶全偏联系数来分析。

对三元联系数μ=0.41+0.11i+0.48j,我们来计算它的二阶全偏联系数。

根据式(1)-(4),(6)得:

0.80876+0.79364j,

在j=-1时,∂2±μ=0.01512>0,这个结果表明三元联系数μ在微观层次上的演化趋势是弱正向趋势,因此，假以时日,或者人为干预可以让事件朝着正确(此例为“认可”)方向发展。

(二)“跪拜”的德国逐渐回归到正常国家

在反法西斯胜利70周年之际,偶然在中国教育报上读到德国前总理的“惊世一跪”的民意调查结果,结合三元联系数的偏联系数相关知识对这些数据进行分析,分析结果发现基本符合历史的发展规律。从文献[12]可以看出,德国对二战的反思是漫长的、痛苦的渐进过程。反思不仅是体现在形式上,更重要的是体现在思想和精神层面上。

从以上分析可以看出,“惊世一跪”事件属于系统第二平衡态,此时无论事件朝正向、负向发展都需要外界干预,而德国选择了正向干预,其典型事件有:在二战结束40周年之际德国元首明确将1945年5月8日德国“战败日”确定为德国“解放日”,这一天也被认定为世界人民摆脱法西斯残忍的非人道行径中重回解放的日子;冷战终结的重要标志性建筑物之一的“柏林墙”(即“反法西斯防卫墙”)也在反法西斯胜利45周年之际倒塌,这道伤痕累累的“柏林墙”的倒塌也是推动该事件朝正确方向发展的因素之一;2015年即反法西斯胜利70周年之际,随着德国前总理的双膝在二战遇难纪念碑前的跪拜,加快了德国从战败回归到正常国家的进程。总之,德国对二战的反思非常彻底,因此德国的以时间换空间的行为也得到了邻国以及世界人民的谅解,这与日本对二战的态度形成强烈的反差。

三、结论

偏联系数是联系数的一种伴随函数，它与联系数本身为我们提供了丰富的信息，这为我们揭示研究对象的联系和运动规律提供了可以分析和研究的方法和途径。

(一)根据全偏联系的数值能粗略的判断出事物的发展趋势。但是,由于偏联系数中不确定系数i取值的不确定性使然,根据上述准则得到的趋势判断结论仍会具有一定程度的不确定性;如何减少趋势判断结论的不确定性,增强趋势判断结论的可信性,通常需要作全面和深入的分析,这些分析包括对原联系数各联系分量数据构成的结构分析,各联系分量的成因分析,以及原始数据所在环境的分析等等。因为根据集对分析理论,联系数中以不确定系数形式存在的i,实质上该联系数所在环境的所有不确定性因素所构成的不确定性子系统的“代表”,全面和客观地分析这个不确定性子系统,才能给出较好的i值,才能减少趋势判断结论的不确定性,提高结论的客观性和可信性。

(二)若三元联系数的二阶全偏联系数∂2±μ处于临界点时,事物发展趋势较为复杂。在文中所举例子说明当时德国民众对前总理“惊世一跪”的认识发展,不仅取决于当时的认识,还取决于认识环境的日后变化。如果希望事物向正方向发展或向负方向发展,需作人为干预。事实证明,“惊世一跪”事件朝德国民众“认可”即正向发展，德国政府作了人为干预。标志性的事件有：现实中德国将“战败日”确定为“解放日”;德国在冷战时期的“反法西斯防卫墙”(柏林墙)的倒塌;德国前总理在二战遇难纪念碑前的跪拜等等。

(三)对三元联系数的全偏联系数接近临界点时,事物发展在临界趋势,这时,一方面可以认为受外力的影响比较大,另一方面,又可以看作是联系数刻画的事物内在发展规律的作用,因为从本质上说,事物发展是由量变到质变的过程,在联系数中,这个过程集中反映在不确定系数 i的表现上。