基于Canny的边缘检测改进算法

李 凌

图像边缘是图像的主要特征之一，边缘检测是图像分析、识别的基础.图像边缘在灰度上表现为不连续性，是像素灰度值有屋顶变化或阶跃变化的像素值的集合.灰度图像的梯度研究是目前边缘检测的主要方向.灰度图像的梯度在数学上表现为微分，常用的边缘检测算子有Robert、Sobel、Prewitt等 一 阶 微 分 算 子 ，LapLacian、Marr_Hildret等二阶微分算子，这些算子通过把灰度图像与一定大小的模板进行卷积，以提取图像边缘，这种方法易于运行，具有较好实时性，但是提取的边缘粗糙，容易受噪声的干扰.

John F.Canny于1986年提出Canny边缘检测算子.在检测边缘时，Canny算子可满足信噪比、定位精度和单边响应［1］3个最优准则.Canny算子是基于最优化算法的检测算子，与传统微分算子相比，不仅具有较大的信噪比，还具有相当高的精度，因此，广泛应用于数字图像处理领域，但是Canny边缘检测对噪声非常敏感，易受光照变化影响，检测过程中，利用固定参数的高斯滤波器平滑图像，易造成过度平滑，模糊图像边缘，造成细节信息丢失；没有统一标准选取高低阈值，通常是人为设定［2］，算法的适应性受到限制.近年来，许多学者提出了基于Canny算子的改善算法.文献［2］采用根据图像的均值与方差确定高低阈值，文献［3］和文献［4］采用自适应滤波器代替传统Canny算法中的高斯滤波器，文献［5］采用小波变换增强图像的边缘，消除传统Canny算法对弱边缘、不连续边缘图像边缘检测效果不好的弱点.

本文提出一种改进的Canny边缘检测算法，用形态学滤波代替高斯滤波平滑图像，借鉴Sobel算子并拓展45°和135°方向梯度模板，计算梯度和幅值，根据图像的灰度均值与方差自动计算高低阈值，改进算法在边缘检测和抗噪声方面效果良好.

1 传统Canny算法

方差σ的取值决定图像平滑的程度，若σ较大，图像信噪比较高，边缘定位精度较低；σ取值较小，情况与之相反，因此，σ的合理取值是图像边缘定位精度和信噪比的关键因素.

（2）计算梯度幅值与方向.传统Canny算法采用2×2邻域一阶偏导有限差分计算滤波后图像I(x,y)的梯度幅值和方向.计算x和y方向的偏导数Ex(x,y)、Ey(x,y)方法分别如式（2）、式（3）所示：

计算梯度幅值和方向的方法分别如式（4）、式（5）所示：

Canny边缘检测算法的基本思想是：首先，采用高斯函数的任意方向的一阶导数平滑图像；然后，计算平滑后的图像的梯度幅值和方向，采用非极大值抑制技术来抑制局部区域的干扰值；最后，设定高低阈值去除虚假边缘，连接真边缘.算法实现如下：

（1）高斯滤波平滑图像.用高斯滤波器平滑图像，以抑制噪声.二维高斯函数如式（1）所示：

（3）非极大值抑制.非极大值抑制其实质就是保留幅值局部变化最大的点，抑制局部区域内的干扰值，以更加准确定位边缘.它的基本思想是：图像I(x,y)上点(i,j)的梯度幅值E(i,j)与沿着梯度线方向上的两个相邻像素点的梯度幅值进行比较，若小于，则认为该像素点为不是边缘点，将其E(i,j)置为零.

（4）双阈值提取边缘.Canny算法使用高低阈值Th和Tl对非极大值抑制过的图像进行分割.首先，根据先验知识选用Th和Tl；然后，扫描候选边缘图像，对于候选边缘图像中的(x,y)，若E(x,y)大于Th，则认定 (x,y)是边缘点，若E(x,y)小于Tl，则认定(x,y)不是边缘点，对于梯度值介于高低阈值之间的候选边缘点，即Tl＜E(x,y)＜Th，则需依据边缘的连通性进一步判断，连成轮廓［6］.

2 改进的Canny边缘检测算法

针对传统Canny边缘检测算法的不足，本文进行了如下改进：用形态学滤波代替高斯滤波，进行降噪处理，解决方差σ不能自适应的问题；采用x，y，45°，135°四个方向Sobel算子计算梯度和幅值，解决传统Canny算法因采用有限差分计算梯度和幅值而对噪声敏感，易丢失一些真实边缘的问题；根据图像的灰度均值与方差自动计算高低阈值，解决人工选用阈值，灵活性低的问题.

2.1 复合数学形态学滤波

灰度图像形态学包括膨胀、腐蚀、开、闭运算，各个运算的定义如下：

①膨胀运算：

③开运算：

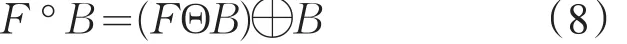
④闭运算：

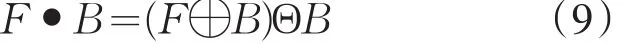
其中：F(x,y)为灰度图像，B(s,t)为形态学结构元素.

形态学滤波的关键是选取合适的结构元素，构造形态学滤波算子.在Canny算法中引入形态学滤波平滑图像，其实质是用某种尺度的结构元素对图像顺序进行开运算、闭运算，去除噪声.开运算通常用于去除比结构元素小的亮细节，闭运算通常用于去除比结构元素小的暗细节［7］.②腐蚀运算：

设C为平滑后的图像，两种常见的形态学滤波算子可以表示为：

将以上两种滤波算子结合起来，构造出一种复合形态学滤波器［8］.本文采用式（12）所示的复合形态学滤波器.

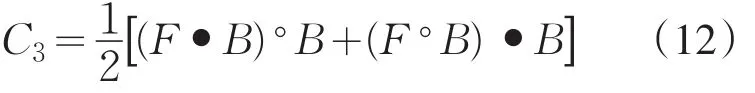
当结构元素B的尺度太小时，开运算可以去除比其更小的明亮细节，能够有效保持图像边缘的细节信息，当B尺度较大时，闭运算可以去除比其更好的暗细节，会模糊掉许多细节信息，但是去噪能力较强，因此使用开、闭交替运算，既可以有效去除噪声，获得很好的平滑效果，也能保持边缘细节信息.

本文构造的多结构元素的复合滤波器如下：

2.2 梯度幅值计算方法

传统的Canny算法使用2×2有限差分计算梯度值［9］，该方法对边缘定位较好，但是对噪声敏感.学者们对此进行了相关研究，文献［5］提出计算3×3的8邻域内x方向、y方向、45°和135°四个方向的一阶导数差分计算梯度值，文献［6］针对8邻域内的45°或135°旋转可变的缺点，对x方向、y方向的差分进行了改进，兼顾了边缘定位和抗噪要求，但是计算复杂.本文在传统Sobel算子的水平、垂直两个方向模板的基础上，加入45°和135°方向模板来计算梯度幅值，Sobel算子四个方向的模板如图1所示.

将图1中的模板分别与滤波后的图像进行卷积，可得到四个方向的梯度分量Px(x,y)、Py(x,y)、P45°(x,y)、P135°(x,y)，梯度幅值由式（14）求出：

图1 Sobel算子四个方向的模板

2.3 阈值求取算法

Canny边缘检测算法的高低阈值的大和小直接决定着检测到的边缘信息的少和多，高阈值越大，保留的边缘信息越少，可有效抑制伪边缘，但是丢失一些边缘信息［2］；相反，若阈值越小，保留的边缘信息越多，但是伪边缘也会相应增加.为检测出图像的更多边缘细节，在选取高阈值时不仅应考虑图像的整体特点，也应该考虑图像的局部特点；图像的平均方差能够反映图像的整体变化情况，局部方差反映的是局部变化情况.因此，在选取阈值时，综合考虑图像的灰度变化（平均方差Eave）和图像本身的灰度信息（平均灰度Fave），这样可以检测到更多的边缘信息，本文获取高阈值的方法如式（15）所示：

引入系数k是为了解决Eave与Fave直接比值所造成的伪边缘信息过多的问题，实验表明，k∈(0.2，0.5)时，检测效果最好.

2.4 算法描述

首先采用复合形态学滤波器平滑图像，去除噪声，采用Sobel算子计算梯度和幅值，进行非极大值抑制，根据图像灰度信息确定高低阈值，检测、连接边缘.

算法描述如下：

①将欲检测的灰度图像F与形态学结构元素进行开闭运算，去除噪声，得到滤波后图像F′；

②根据Sobel算子的四个方向梯度模板计算梯度和幅值；

③对图像F′进行非极大值抑制；

④根据图像灰度平均方差Eave和平均灰度Fave确定阈值；

⑤检测并连接边缘.

3 实验结果与分析

为了验证算法的有效性，分两种情况在软硬件环境为：Intel 2.5GHZ双核CPU，4GB内存，M atlab2012B的条件下进行仿真实验：无噪声情况，加入噪声情况，将本文的算法与传统的Canny算法进行比较.

图2 无噪声情况下Lina图像

图3 加入均值为0、方差为0.1椒盐噪声Lina图像

对比实验结果可以看出，传统算法对边缘表现得笼统，而本文算法可检测出更多的边缘细节；图2和图3的（b）中，左边的长杆出现断裂情况，脸庞有明显断裂；由于对灰度缓慢变化的区域检测到的信息少，连续性差，导致冒顶和头发细节部分也不好；而从图2和图3的（c）中可看出，左边的长杆、脸庞、头发检测的情况明显比传统算法好；对比图2和图3可看出，本文算法受噪声影响较小，定位更准确，比传统算法的边缘清晰，边缘检测效果较好.

4 结论

针对传统Canny边缘检测算法的效果易受噪声、光照等因素的影响，人工选择参数，自适应性差等不足，对传统的Canny算法进行了改进，用复合形态学滤波器代替高斯滤波器，降低噪声影响；采用拓展方向模板的Sobel算子计算梯度，提高边缘定位效果；根据图像的灰度均值和方差选取阈值，避免人为选择阈值的局限.实验结果表明：改进算法比传统Canny算法具有更好的检测效果和抗噪性能.