目标大小对单臂和双臂动作控制特点的影响

王超懿，邹晓峰，朱寒笑，Charles H.Shea

日常生活中的很多动作，如穿针、系鞋带、系扣子需要我们两侧手臂协调配合去完成。这些动作任务往往对动作的准确性有所要求。设计本试验的目的，是为了研究目标的大小对于手臂控制特点的影响。

许多动作技能，如弹钢琴或投篮等，运动者需要同时兼顾速度和准确性。在这些运动技能中，需要在速度和准确性之间做出权衡。运动者要么牺牲速度来提高准确性，要么牺牲准确性以提高运动的速度。Fitts定律在量化速度—准确性现象方面发挥了重要作用[1]。FITTS发现，运动者手臂在2个目标区域来回移动时，目标区域的宽度减少或运动幅度的增加都会导致目标间平均运动时间的增加。FITTS提出了一个对数方程来测量动作难度，称为难度系数（ID-index of difficulty），即ID=log2（2A/W），其中A代表两目标中心间的距离，W代表目标宽度。FITTS发现，目标运动的难度系数（ID）与运动时间（MT）成线性关系：MT=a+b*（ID）。运动时间和难度系数的关系被称为Fitts定律。Fitts定律被在很多互惠目标运动上进行了测试，并被验证有效[2-5]。

许多学者系统地研究了不同难度系数下右臂（单臂）目标运动的控制过程，并指出高ID和低ID动作在运动学特征上的不同[6-11]。对于低难度系数的运动，动作的轨迹平滑并且协调，一个动作加速和减速过程的分配比较平均，在目标处转折的停留时间很短或几乎为零。对于高难度系数的运动，动作的轨迹不那么平滑且不协调，一个动作的大部分运动时间都被分配到减速的阶段，在目标处转折的停留时间会长一些。伴随ID的增加，目标运动的运动学特征可以被描述为一种由非连续性运动到周期性运动的转换。周期性控制具有开环控制的特征，反映在较短的运动和停留时间以及加速百分比和协调指数的增加。非连续性控制具有闭环控制的特征，反映在较长的运动和停留时间以及加速百分比和协调指数的下降[7]。BUCHANAN等[7]指出，周期性控制和非连续性控制特点的转换主要发生在ID为4.0～4.9的区间。

相比于单臂目标运动研究，双臂目标运动研究的文献并不多见。KELSO等[12]研究发现，当双臂同时做不同ID目标运动时，Fitts定律不再适用。在KELSO等[12]的经典双臂目标试验中，受试者被要求将2个食指从中线位置尽可能快和准确地移动到位于左右2侧的2个目标区域。目标区域的大小和到中线的距离，致使2手臂的运动具有相同或不同的ID。当2目标的ID不同时，用于执行低ID动作的手臂运动时间被延长，以匹配执行高ID动作的手臂运动时间。作者得出的结论是，双臂同时做不同ID运动时，内在控制机制限制两侧手臂去做协同运动。也就是说，双臂运动在某些情况下比单臂运动更难完成。

有关双臂协调运动研究，通常是通过让左右两侧肢体做相同或不同模式的周期性屈伸运动来完成[13-18]。双臂协调文献一再表明，同相位（in-phase）协调模式是高度稳定的，而其他相位协调模式运动稳定性相对弱，并更难完成[16，19-20]。同相位的模式，指双臂的协同肌同时运动；反相位的模式，指双臂的拮抗肌同时运动[14]。当运动者在执行同相位或其他相位协调模式运动时，增加运动频率，会导致运动者的运动模式从其他类型模式（如反相位模式、有90°相位差、双臂做不同频率的模式等）不由自主地转换至同相位模式，而不会导致从同相位模式转换至其他类型模式[21]。有90°相位差的协调模式，可以被理解为一侧手臂总是保持晚于另一侧手臂1/4周期做同样的动作（一次屈伸运动代表一个周期）。通过扫描有0°～180°相对相位的试验，YAMANISHI等[20]发现，所有被测试的2侧手臂的相位误差及其变率都比同相位（0°相对相位）模式高，虽然反相位（180°相对相位）动作较其他（非同相位）模式稳定。研究者得出结论，双臂协调运动的内在机理是，同相位和反相位以外的协调模式都相对不稳定，倾向于向同相位和反相位模式转换[15]。

近些年的研究表明，在完成同相位和反相位之外的相对相位模式的困难主要是由注意力和感知觉的限制造成的。然而，这些限制因素可以通过提供给受试者一个整合了双臂关系的反馈信息，使限制因素最小化。如Lissajous视觉反馈[22-25]，被证明能够提供给受试者一些有效的信息。这些有效的信息，能够帮助受试者通过几分钟的练习就可以快速和有效地完成各种各样双臂协调任务。这些双臂协调任务包括了同相位和反相位之外的其他相位的协调模式。Lissajous反馈，将双臂的位置整合到屏幕上的一个点上[22-25]。受试者通过在屏幕上指定的轨迹模版上移动光标，可以完成很多不同模式的双臂协调任务。

从现有的国内外文献来看，尽管很多学者研究了Fitts定律，而从双臂的角度对Fitts定律进行的研究还很有限[12，23-25]。通过改变在Lissajous视觉反馈运动模板呈现方法，以及改变在Lissajous视觉反馈平面上目标的位置和大小，本研究将单、双臂运动和Fitts运动的特点结合起来。通过比较单双臂同相位目标运动的控制特点，从而理解双臂同相位目标运动的控制特点。

1 研究对象与方法

1.1 研究对象

本试验选取Texas A&M大学的16名[6男，10女，年龄（19.88±1.15）岁] 健康成年受试者参与本试验。受试者之前没有做过类似的试验。我们用修改版的Coren偏手性评价量表[26]来评价受试者的偏手性。其中，一名受试者偏手性为左利手，其余受试者偏手性均为右利手。

1.2 研究方法

1.2.1 仪器设备 试验的仪器包括2个水平控制杆，它们分别由2个近乎无摩擦的转轴固定在一个桌子上。一个控制杆固定在桌子的左侧，由受试者的左侧前臂来控制；另一个控制杆在桌子的右侧，由受试者的右侧前臂来控制。旋转轴允许控制杆在桌面以上的水平面转动。杆的前端安装了垂直手柄。受试者需要将肘部置于转轴上方并将前臂与控制杆对齐，然后手握手柄（手柄的位置可根据臂长调整）。控制杆的旋转角度数据，由安置在转轴上的角度传感器测定。角度传感器的采样频率为200 Hz。实时数据将用于控制视觉反馈显示面上的指针（光标）的位置。将指示控制杆位置的指针，通过受试者后上方的投影仪投射到受试者前方2 m的墙上。在视觉反馈显示面上，伸或屈左臂会使光标相应向上或向下移动；而屈或伸右臂使光标相应向左或向右移动。一个木制框架被用来防止受试者在试验中看到自己的手臂，从而使受试者只能通过视觉反馈显示面上的光标来调整自己手臂的移动。

1.2.2 测试方法 受试者坐在桌子前面的一个可调节高度的椅子上。在双臂或单臂的情况下，2个水平、垂直、或成对角位置的目标框被投影在受试者前方的屏幕上（见图1）。受试者需要尽可能快并准确地在2目标框间来回移动光标。准确性，是指要求受试者在目标框内转换光标的运动方向，而不是在超过或没有达到目标框时转换。在每个任务中，2个目标框的大小相同。2个目标框中心之间的距离（A）被设定为40°和目标框宽度（W）被分别设定为14.14°、10°、7.07°、5°、3.54°、2.5°、1.77°和1.25°。根据Fitts定律（ID=log2（2A/W）），会对双侧或一侧手臂形成难度系数（ID）为2.5、3、3.5、4、4.5、5、5.5和6的屈伸任务。一种情况下，试验以ID升序的方式进行；另一种情况下，试验以ID降序的方式进行。代表每一个ID的目标将会出现7.5 s然后立即变换到下一个ID。因此，每次试验尝试的时间为60 s。试验分为2种情况：双臂的情况和单臂的情况。单臂的情况又分为左臂和右臂的情况。试验还分2个难度系数顺序：升难度系数顺序和降难度系数顺序。在升难度系数和降难度系数的情况下每种情况分别做4个试验尝试。每种情况的最后1次试验尝试的数据将会被用于数据分析。

1.2.3 数据分析 手臂的单臂控制特点可以通过以下4个指标进行评估：运动时间（MT，Movement Time）、停留时间（DT，Dwell Time）、加速百分比（PTPV，Percent Time to Peak Velocity）和协调指数（H，Harmonicity）。手臂的双臂控制特点可以通过以下2个指标进行评估：平均相对相位和平均相对相位的变率。

在数据分析进行之前，将每个试验尝试（60 s）的位移序列分割成8段（每个7.5 s）。每段代表一个ID情况。在每个ID位移序列段的基础上，计算以上4个指标。

运动开始时间点、结束时间点和加速百分比，是在每个半周期峰值速度基础上计算的。每个半周期代表一个屈或伸的动作。在每半个周期内，运动开始时间点（Onset）是从峰值速度（PV，Peak Velocity）开始向后追踪到第1个小于5%峰值速度的时间点；运动结束时间点（Offset）是从峰值速度开始向前追踪到第1个小于5%峰值速度的时间点。在目标运动中，增加难度系数将导致用于准备后续周期运动的（在目标区域转折动作的）时间延长[27-28]。这段时间被称为停留时间，停留时间的公式是：DT=Onseti+1-Offseti；运动时间的方程是：MT=Offseti-Onseti；加速百分比的公式是：PTPV=（PVi-Onseti）/（Offseti-Onseti）。

加速百分比，用以指示手臂每个屈或伸运动有多少比例的时间用以加速或减速。一般来讲，难度系数比较低的运动加速和减速的分配较平均，而难度系数比较高的运动大部分时间都用以减速。在减速的这段时间里，受试者利用视觉反馈不断地调节手臂与目标之间的距离。

为了计算协调指数，在位移时间序列中，位移为0的2个相邻点之间的区域被定义为协调指数计算窗[7，9]。每一时间窗包括一个屈-伸（或伸-屈）的转换。在时间窗内，在过滤后的加速度时间序列中可以观测到所有的转向点。当在一个计算窗内所有的转向点为正值或者负值时，协调指数为加速度绝对值最小的转折点与加速度绝对值最大的转折点的比值。当一个计算窗有且只有一个加速度单峰值（转向点）时，协调指数为1，表示肢体做谐波运动（harmonic motion）。如果加速度迹线在该计算窗内由负到正穿越零点（或由正到负穿越零点），协调指数的值为0，表示非谐波运动（inharmonic motion）。最后，对每个时间窗下的协调指数求取平均值，得到一个ID情况下的协调指数的平均值。协调指数的平均值将与经验值0.5进行比较，用以判断是否发生了周期性到非连续性运动的转换（或反之亦然）[7，10-11]。协调指数的平均值越大（＞0.5），单臂的运动模式与周期性运动越接近；协调指数的平均值越小（＜0.5），单臂的运动模式与非连续性运动越接近。

在双臂动作任务的每次尝试中，每侧手臂的相位角（phase angle）θ被测量，计算方法同KELSO等[19]和WANG等[25]研究：在双臂动作任务的每次尝试中，每侧手臂的连续相对相位（a continuous relative phase measure）c被计算，以检验手臂在完成动作任务时的时空协调情况。若要计算连续相对相位，首先要计算在每个采样点上的连续相对相位角。连续相对相位角是根据代表每侧手臂的水平杆的位移（x）和速度时间序列计算得出的。位移（x）和速度时间序列被平均居中，并且重新调整到-1～1的范围。对于每侧手臂，每个采样点的连续相位角的计算方法如下：

然后，用每个采样点对应的左臂的相位角减去右臂的相位角得出相对相位差：RPi=θ左i-θ右i。取一次尝试中采样点相对相位差的平均值，得到平均相对相位（relative phase）。平均相对相位用以指示双臂的耦合（coupling）程度。相对相位值越小，指示双臂的协同运动就越紧密。相对相位的变率（relative phase variability）为一次尝试中每个采样点相对相位差的变率，用以反映双臂协调模式的稳定性[19]。

反应单臂控制特点的4个指标将通过单双臂（单臂，双臂）×ID（2.5、3、3.5、4、4.5、5、5.5、6）×左右臂（左，右）×顺序（升难度系数，降难度系数）的方差分析。其中，所有情况为重复测量因素。丹肯新多重范围测试（Duncan's new multiple range test）和简单主效应分析（simple main effects）被用于进一步分析显著的主效应。所有的测试将使用0.05的显著水平。

反应双臂控制特点的2个指标将通过ID（2.5、3、3.5、4、4.5、5、5.5、6）×顺序（升难度系数，降难度系数）的方差分析。其中，所有情况为重复测量因素。丹肯新多重范围测试和简单主效应分析被用于进一步分析显著的主效应。所有的测试将使用0.05的显著水平。

2 结果

双臂和单臂在不同ID和顺序（升或降ID）下，反应手臂控制特点的指标的描述性数据见表1。

表1 双臂和单臂指标的描述性统计Table 1 Bimanual and Unimanual Descriptive Statistics

2.1 运动时间

运动时间的分析检测到单双臂的主效应[F（1，14）=32.34，P＜0.01] ，ID 的主效应[F（7，98）=163.85，P＜0.01] 和顺序的主效应[F（1，14）=4.94，P＜0.05] 。此外，顺序×ID交互作用[F（7，98）=9.91，P＜0.01] 显著（见图2A）。双臂情况（M=0.904 s）的运动时间比单臂情况（M=0.637 s）长。顺序×ID交互的简单主效应分析的结果表明，随着ID每增加1个单位，2个顺序的运动时间都增加。顺序×ID交互作用的简单主效应分析的结果也表明，在ID从5～6的情况下，升ID顺序的运动时间要比降ID顺序的运动时间短，但是在其他ID情况下，2个不同顺序之间运动时间差异不显著。

2.2 停留时间

停留时间的分析检测到单双臂的主效应[F（1，14）=10.23，P＜0.01] 和 ID 的主效应[F（7，98）=41.13，P＜0.01] 。另外，单双臂×ID交互作用[F（7，98）=5.30，P＜0.01] 显著（见图 2B）。单双臂×ID交互作用的简单主效应的分析结果表明，随着ID从4到6，每增加1个单位，双臂情况的停留时间增加，但是ID从2.5到4.5之间的停留时间差异不显著，随着ID从4.5到6每增加1个单位，单臂情况的停留时间增加，但ID2.5到5之间ID间停留时间的差异不显著。单双臂×ID交互作用的简单主效应的分析结果也表明，双臂情况的停留时间在ID从5.5～6处比单臂情况更长，但单双臂停留时间的差异在ID值2.5～5处不显著。

2.3 加速百分比

加速百分比的分析检测到单双臂的主效应[F（1，14）=26.28，P＜0.01] 和ID的主效应[F（7，98）=71.92，P＜0.01] 。此外，顺序×ID交互作用[F（7，98）=3.77，P＜0.01] 显著（见图2C）。单臂情况的加速百分比（M=41.121%）高于双臂情况（M=34.788%）。顺序×ID交互作用的简单主效应分析结果表明，不论是升ID顺序还是降ID顺序，随着ID增加，加速百分比时间减少。顺序×ID交互作用的简单主效应分析结果还表明，在ID为2.5时降ID顺序的加速百分比大于升ID顺序，但是在ID为6时升ID顺序的加速百分比大于降ID顺序。然而，在ID为3～5.5时没有检测到2个顺序的加速百分比之间的差异。

2.4 协调指数

协调指数的分析检测到单双臂的主效应[F（1，14）=19.45，P＜0.01] 、左右臂的主效应[F（1，14）=8.64，P＜0.05] 和ID的主效应[F（7，98）=113.79，P＜0.01] 。另外，单双臂×ID交互作用[F（7，98）=4.85，P＜0.01] （见图2D）是显著的。左侧手臂的协调指数（M=0.392）高于右侧手臂（M=0.337）。单双臂×ID交互作用的简单主效应分析结果表明，双手情况的协调指数随着ID从2.5～5之间每增加1个单位会显著下降，但ID在4.5～6之间的差异不显著。然而，对于单臂情况下的所有ID，每增加1个单位，协调指数降低。单双臂×ID交互作用的简单主效应分析结果还表明，双臂情况下的协调指数值在ID处于2.5～5的范围内低于单臂的协调指数，但单双臂协调指数的差异在ID值处于5.5～6之间时并不显著。

2.5 相对相位

平均相对相位的分析检测到ID的主效应[F（7，105）=32.34，P＜0.01] （见图3）。丹肯新多重范围测试结果表明，ID处于2.5～3范围内的平均相对相位值显著高于其他ID，然而在ID处于2.5～3区间和3.5～5区间，相邻ID之间的平均相对相位差异并不显著。

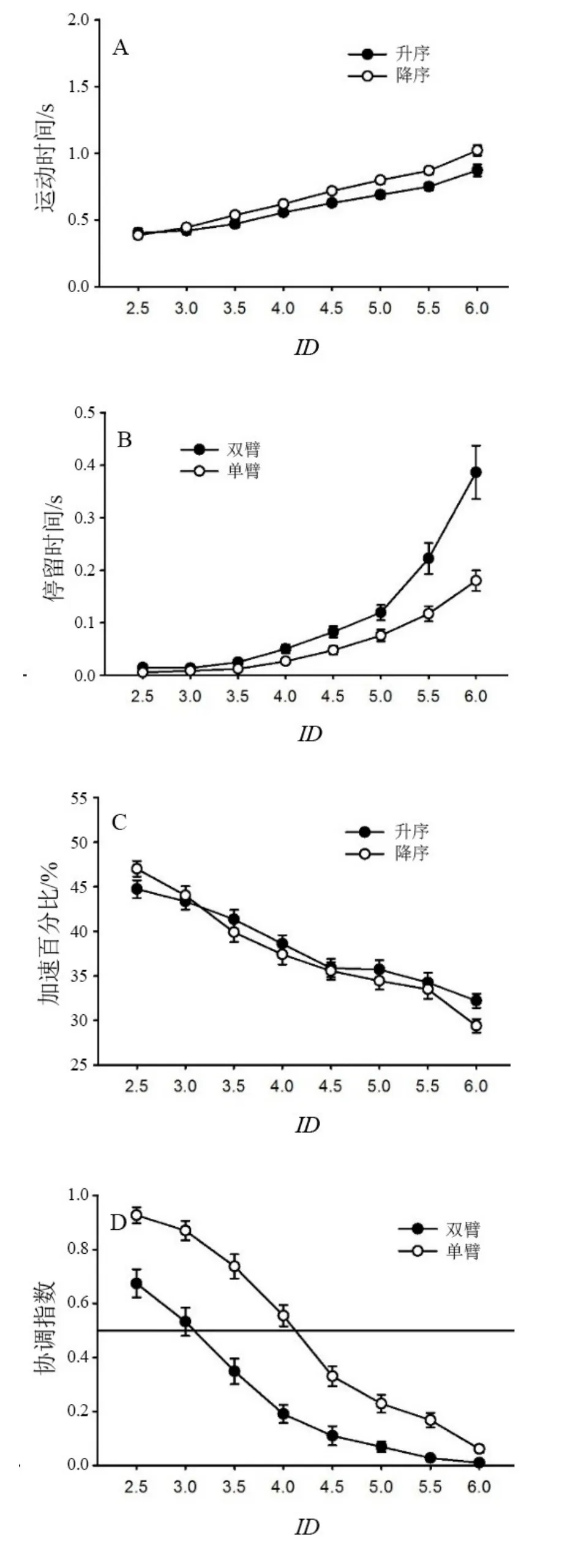
图2 4个单臂指标Figure2 Four Unimanual Results

图3 不同ID下的平均相对相位Figure3 Mean Relative Phase as a Function of ID

2.6 相对相位变率

方差分析结果显示，相对相位变率的任何主效应或交互作用都不显著。

3 讨 论

试验数据表明，无论是升ID还是降ID顺序，还是单臂或双臂情况，随着ID增加，手臂的运动特征逐渐从周期性转变为断续性，并随着ID减少而从断续性运动切换到周期性运动。控制特点中的这种切换，可以通过运动时间和停留时间的增加以及加速百分比和协调指数值的减少来指示（见表1，图1）。本试验中，单臂和双臂的整体控制特点，与BUCHANAN等和GUIARD用右侧手臂测量的研究结果相一致[7，9-10]。但是，在特定的ID情况下，单臂和双臂目标运动之间的运动学控制也存在一些差异。

在运动时间的数据分析中发现显著的单双臂效应。当目标宽度在同一个试验尝试中被放大或缩小时，双臂的目标运动比单臂目标运动在所有的难度系数下的运动时间更长。在停留时间的分析中发现了显著的单双臂×难度系数的交互作用。单双臂×难度系数的简单主成分分析结果说明，两侧手臂在高难度系数下，双臂目标运动都比单臂目标运动的停留时间长。以上运动时间和停留时间的结果表明，双臂的目标运动比单臂目标运动需要更多感知觉信息处理的要求，特别是在高难度系数的情况下。

在协调指数的分析中发现了显著的单双臂×难度系数的交互作用。从协调指数的图中（见图2D）可以看出，协调指数跨越0.5的区域在双臂的情况下发生在ID4和ID5之间，但是在单臂的情况下发生在ID3和ID4之间。BUCHANAN等[7]指出，当系统增加或减少ID时，控制策略由周期性向断续性转换的协调指数的临界值为0.5。协调指数的分析结果说明，在双臂的情况下，手臂周期性和断续性控制策略间的转换更容易出现在高ID区域。这表明，在相同难度系数下，双臂情况比单臂情况更需要非连续性的控制策略。这是由于，双臂共同做目标运动使受试者占用更多的运动资源，导致使用非连续性控制策略的趋势更为显著。

在平均相对相位的分析中发现了显著的ID主效应。从平均相对相位的图中（见图3）可以看出，平均相对相位的耦合程度随着难度系数的增加不断增强（值变小）。在相对相位的变率分析中，任何主效应和交互作用都不显著。这表明，增加难度系数虽然使双臂的耦合变得更紧密，但是并没有使双臂的协调变的更加稳定。

4 结论

（1）无论是升ID还是降ID顺序，还是单臂或双臂情况，随着ID增加，手臂的运动特征逐渐从周期性转变为断续性，并随着ID减少而从非连续性运动切换到周期性运动。（2）双臂的目标运动比单臂目标运动需要更多感知觉信息处理的要求，特别是在高难度系数的情况下。（3）在相同难度系数下，双臂情况比单臂情况更需要非连续性的控制策略。这是由于双臂共同做目标运动，使受试者占用更多的运动资源，导致使非连续性控制策略的趋势更为显著。（4）增加难度系数（目标变小）虽然使双臂的耦合变得更紧密，但是并没有使双臂的协调变的更加稳定。