乘用车冷却风扇流量与噪声研究

龙祖荣,谭明香，万涛，郦志俊

(1.东风柳州汽车有限公司，广西柳州 545005;2.江苏超力电器有限公司，江苏镇江 212300)

0 引言

轴流风扇噪声是车辆冷却系统主要的噪声源之一。亚音速工况下，偶极子脉动力辐射噪声是风扇主要的气动噪声来源，而它又由离散噪声和宽频噪声组成。由于扇叶周期性切割进口区的不均匀气流，产生周期性压力脉动形成离散噪声。宽频噪声来源于风扇旋转时非定常载荷产生的涡流[1]。因此扇叶表面压力波动是气动噪声产生的重要因素。

由于低马赫数流体噪声变化强度比声源涡小很多，工程上普遍采用声源和声传播分离的方法(Segregated Source Propagation Methods，SSPM)计算气动噪声，从而避免直接计算气动声学(Computational Aero Acoustics，CAA)，后者运用高精度湍流模式，消耗大量时间和计算资源[2]。目前国内对风扇外围声辐射研究多集中于扇叶的气动噪声，很少考虑风架对噪声的影响。文中建立完整的风扇总成模型是确保噪声精确性的重要过程。

文中使用流体力学和声学分步耦合方法来计算。采用大涡模型(Large Eddy Simulation，LES)计算瞬时湍流信息，得出扇叶和风架表面非定常压力脉动，通过声学类比FW-H方程得出风扇声源理论定义等价声源，同时运用声学边界元(BEM)方法求解监测点频率特性。

1 求解理论及方法

声源信息的准确性对声传播有决定性影响，而针对旋转机械的风扇声源理论可准确地将压力脉动数据转换为声场计算所需声源模型。

风扇声源坐标系如图1所示。

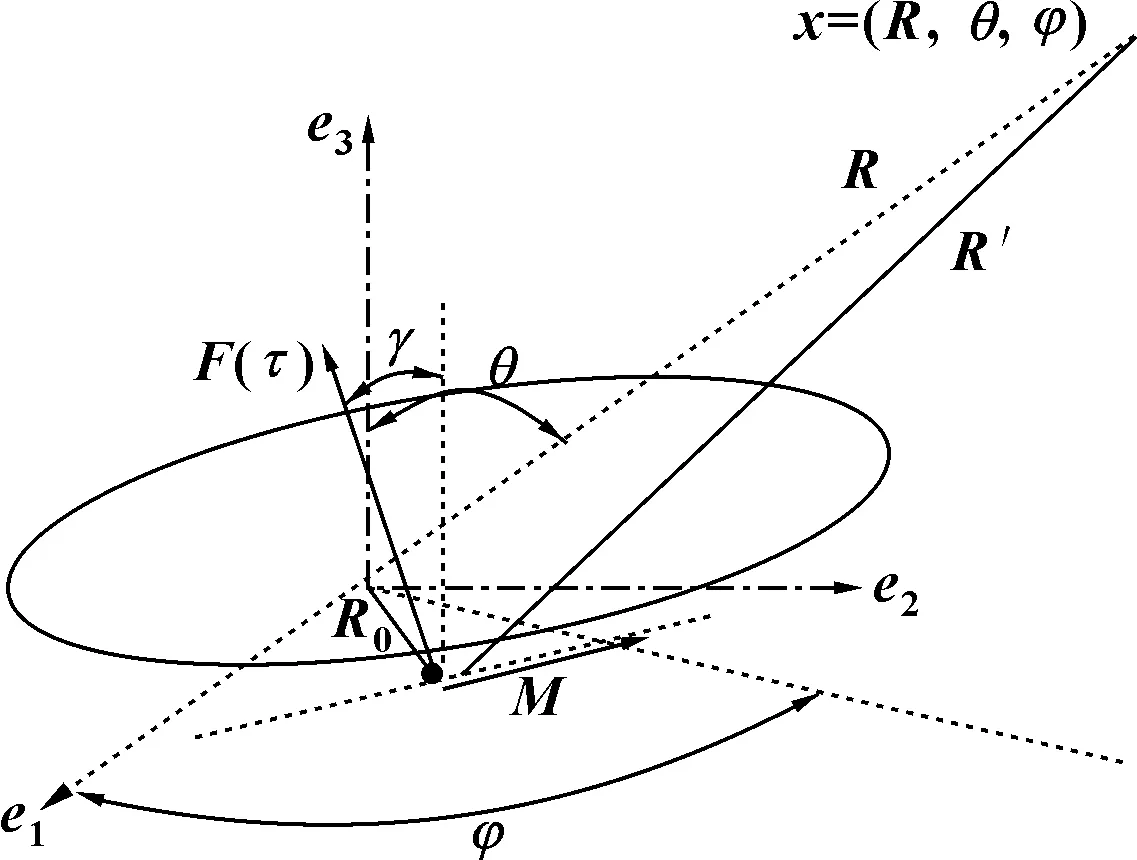
图1 风扇声源坐标系

对于定子-转子的模型(定子在入口),扇叶基频及其谐波时的辐射压力在轴向和切向的贡献量：

(1)

式中：m为谐波数；B为转子扇叶的数量；Ω为转速；R为监测点距离；c0为声速；Fs为扇叶边缘总压力的傅里叶变换；M为转动马赫数；θ、φ、γ的角度定义如图1所示；V为定子扇叶的数目。

扇叶在径向产生噪声贡献量：

(2)

定子在出口处具有类似的声学类比算法。低马赫数下扇叶(转子)表面非定常载荷通过CFD时域瞬态计算得出，进而根据扇叶表面载荷分布对扇叶进行切分，每份等效为一个风扇声源。风架(定子)具有类似等效方法。

声学边界元模型(BEM)是以定义在边界上的边界积分方程为控制方程，通过对边界分元的插值离散，转化为代数方程组求解。它是以微分算子解析的基本解作为边界条件的积分方程的核函数，而它将数值与解析相结合，具有比较高的精度。所以利用这种直接边界元法可精确求解风扇周围封闭网格外声场辐射噪声。

2 有限元模型

根据7扇叶等节距风扇实体总成，建立完整模型，扇叶采用三维坐标点蒙皮的方法绘制。并对模型进行相应的修正与简化，为了不影响有限元模型的精确性，缝合扇叶的表面碎片并清理轮毂中的加强筋与沟槽。简化后风扇总成如图2所示。

图2 风扇总成简化模型

利用CFD软件进行前处理，建立风扇旋转流域、管道区、进口区和出口区4个区域。参数根据试验设备设置，进口区与大气相通，管道长度1.2 m，出口区管道长度3 m，试验设备与CFD流域图如3所示。

图3 流量试验设备与CFD模型

扇叶表面旋转流域是影响流场与噪声的重要区域，扇叶表面区域的网格大小设置3～5 mm。考虑计算资源，流体域使用自适应更强的非结构化网格，对应内外交界面节点，总网格数为350多万，扇叶表面网格如图4所示。

用CFD软件模拟风扇的流场时，进口条件设置为压力入口，静压为0，出口条件的静压根据实际设置为150 Pa。其余壁面条件设置为无滑移壁面。因流体的马赫数小于0.1，故将流体介质定义为不可压缩的气体。采用多重参考系法(Multi-Reference Frame，MRF)，求解风扇在12、12.5、13.5 V工作电压下的流量，对应转速分别为1 900、2 000、2 100 r/min。使用二阶迎风格式计算湍流耗散率、动量和压力等信息，选同时能更好处理流线弯曲程度较大的RNGκ-湍流模型[3]。

图4 扇叶表面网格

3 求解结果与分析

流量试验数据与仿真结果如表1所示。

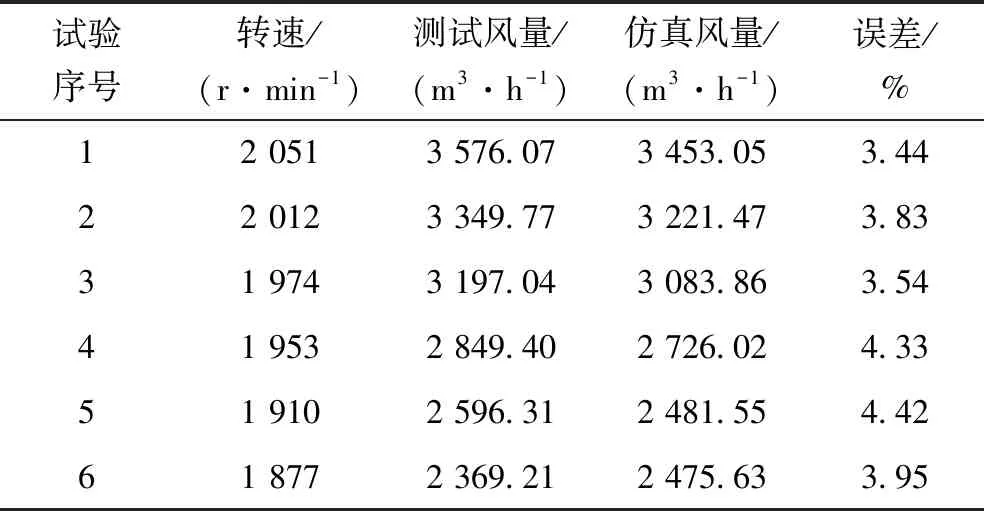
表1 风扇气动性能试验数据

可知，仿真数据和试验数据相比误差在4.5%以内,模型具有较高可靠性。图5为扇叶表面静压图，可知风扇吸风面处呈现较大的负值，吸风面和压风面接触区风压变化剧烈，边缘出现压力集中。

瞬态模拟时，大涡模型使得扇叶尾缘处较大脱落涡分布更为明显。叶尖与叶圈处非定常载荷直接引起的压力面叶顶区域与吸力面上半扇叶区域的压力脉动较大。将扇叶表面瞬时脉动数据通过CGNS格式导入Virtual.lab声学软件中，使用Trap方法对每片扇叶进行4等分切分，最终等效为28个风扇声源。由表面声压分布可得叶尖和叶圈引起的压力脉动大的区域即为噪声主要声源处。

图5 扇叶表面静压

为得出风架对声传播过程影响，导入风扇表面偶极子声源，在其基础上导入风架模型，并定义成声学硬边界条件，认为声波在壁面发生全反射。采用声学边界元模型(BEM)方法在风扇的周围以1 m为半径建立球状的声场，在中轴线上前后1 m处的位置建立场点，模拟试验中麦克风接受位置。在时域条件下,同步求解扇叶离散与宽频噪声，然后利用傅里叶变换将其转化为场点声压级的频谱图。总声压级依据公式(3)所示：

(3)

式中：SPL(i)为第i个1/3倍频中心频率点声压级。

噪声测试使用PULSE多普分析B&K仪器，如图6所示。在半消音室进行测试，环境噪声A计权后约为20 dB(A)。

图6 噪声试验设备

风扇出风口前1 m处噪声大于入风口，试验数据与仿真结果声压级对比如图7所示。

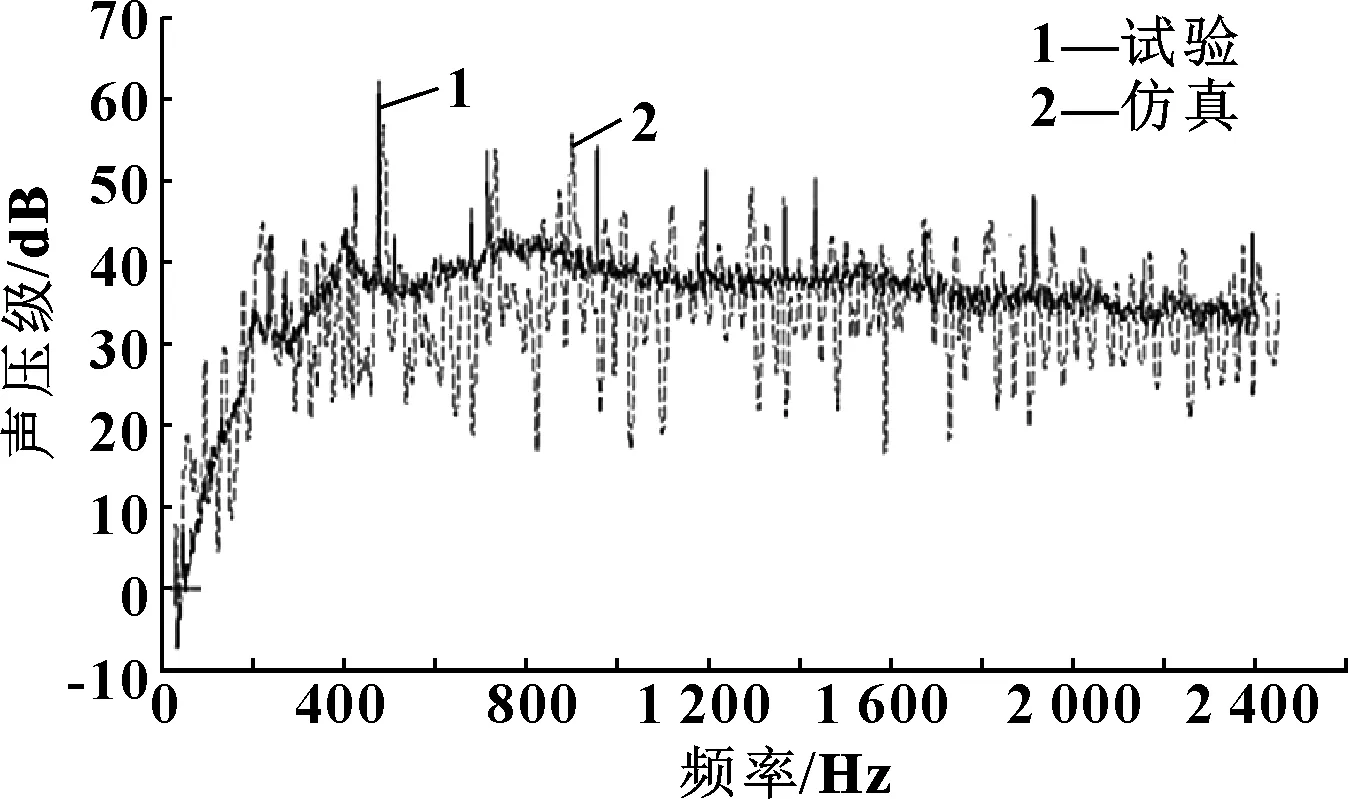
图7 试验与仿真声压级对比

首先可得离散噪声是气动噪声主要组成部分，大小主要取决于叶圈和叶尖的形状及与护风罩的分布关系，宽频噪声较小可忽略。其次风扇气动噪声多集中于低频段，在低频处仿真与试验的基频及一阶谐波吻合很好，高频段差距较大，但影响不大。试验1/3倍频程总噪声在B&K界面直接显示，为71.5 dB(A)，仿真值总声压级依据公式(3)求得为67.1 dB(A)，比试验结果小5.3%。产生误差主要是因为CFD仿真的结果与实际的情形存在一定的偏差，其次是在等效声源的过程中，扇叶按载荷分布规则切分越多，仿真结果越精确，考虑计算资源，等效存在一定误差，同时没有考虑扇叶振动噪声。

4 结论

(1)采用声源和声传播分离的方法，对完整的风扇总成(包括风架)运用 LES(大涡)及风扇声源模型，可较高精度计算轴流风扇的流量及噪声。

(2)风扇旋转时，叶圈与护风罩间隙产生较大回流，对流量产生重要影响。同时此处湍动能较强，叶圈与叶尖表面脉动压力大，是主要噪声源之一。

(3)噪声传播过程中，风架对其具有一定影响，集中在叶圈与护风罩间隙距离与加强筋的阻碍作用，不可忽略。

(4)扇叶高转速时，离散噪声占主导地位，宽频噪声相对较小。合理的不等节距优化可调制风扇的基频及其谐波，有效降低噪声。