基于代价极速学习机的软件缺陷报告分类方法∗

张天伦,陈 荣,杨 溪,祝宏玉

1(大连海事大学 信息科学技术学院,辽宁 大连 116026)

2(深圳大学 计算机与软件学院,广东 深圳 518060)

在软件系统开发领域里,Bug修复[1]是一个十分关键的环节.近几年,随着软件工程项目的规模与复杂度的提升,在软件开发过程中,不可避免地会出现大量的 Bug,为了系统可以正常运行,修复这些 Bug是十分必要的;同时,修复这些Bug的任务量也是非常艰巨的.对于软件系统的开发人员而言,在修复Bug时,最常用的辅助工具就是Bug报告[2].Bug报告是以文本的形式来描述Bug细节的数据,并且根据任务的不同,这些数据被标上不同的标签.但是Bug报告的质量良莠不齐,如果人工地辨别这些Bug报告的质量,无疑又为软件开发带来了沉重的工作量.所以近几年,很多研究者研究如何将Bug报告进行自动分类,其中,Antoniol等人[3]利用文本挖掘技术来对Bug报告进行分类,将Bug报告数据分成需即时处理的Bug和非即时处理的Bug,他们所使用的技术是决策树、对率回归以及朴素贝叶斯等方法.Menzies等人[4]利用规则学习技术将Bug报告分成严重Bug和非严重Bug.Tian等人[5]通过构建一个基于机器学习的预测框架来预测Bug报告的优先级,在这个框架中,他们主要考虑到6个因素:时序、内容、作者、严重程度、产生原因以及相关的Bug.除此之外,还有学者对Bug报告的质量进行分类.Feng等人[6]通过提取Bug报告的特征,来对Bug报告进行高质量和低质量的区分,并且将预测得到的信息提交给软件开发者.为了降低Bug的冗余度,Runeson等人[7]基于信息检索技术提出一种计算Bug报告相似性的方法.类似的,Sun等人[8]提出一种多特征的信息检索模型,其目的也是为了计算Bug报告之间的相似度.近些年,更多的学者关注于 Bug报告数据集的类别不平衡问题,其中,Lamkanfi等人[9]通过人工选择的方法来补充数据集,解决数据集的类别不平衡问题,但是人工选择的方法局限性很大,同时也不适合于实际的工作;Yang等人[10]利用解决不平衡问题的策略来处理Bug报告分类问题,即随机欠采样(random under-sampling,简称RUS)、随机过采样(random over-sampling,简称ROS)和合成少数类过采样(synthetic minority over-sampling,简称SMOTE)方法,这些方法在解决不平衡问题时,其效率明显优于人工选择的方法.

本文的关注点也是自动分类Bug报告,但是我们更加关注于Bug报告分类中存在的一些问题.

首先,在Bug报告数据集里,不同类别的样本的数量不同,而且通常情况下,样本数量之间的差异会造成较大的不平衡度.如果一个数据集的不平衡度较大,那么通过这个数据集训练得到的分类模型的性能就会受到不良的影响.这主要是因为在训练过程中,不平衡的数据集会引导分类器更加侧重于对多数类样例的识别,在更严重的情况下,少数类的样例会被当做噪音点处理.

为了解决 Bug报告中数据不平衡的问题,我们引入了基于代价的分类器训练策略.传统上的分类器的优化求解目标主要是最大化分类结果的精确度,而基于代价的分类器训练策略则是最小化分类器因错误分类而产生的代价.具体地,不同类别的样例被错误分类的代价应该不同,一些较易被分类的样例应该有较小的错误代价,而那些较难被分类的样例应该有比较大的错误分类代价.在最小化整体的错误分类代价时,就会使得分类器更加关注代价大的样例的分类情况.因为传统的分类器模型默认所有样例的分类代价是一样的,所以基于代价的分类器训练方法是对传统方法的一个扩展.

我们选用的分类器模型是极速学习机(extreme learning machine,简称ELM).该方法由Huang等人[11]提出,因为其训练方法的高效性,目前被普遍用于模式识别领域[12].同时,为了解决上面提到的数据不平衡问题,我们用基于代价的分类器训练方法来训练ELM模型,训练得到的模型被称为代价敏感的ELM模型.

Bug报告分类中存在的第 2个问题是:在数据集里,被标记的样本量不充足.传统的分类器大都是通过有监督算法进行训练的,这就要求数据集里的样本既有条件属性也要有与之对应的标签属性.可是,给样本指定正确的标签需要大量的精细的人工标注工作.通常情况下,人工给数据标注类别属性是繁重且耗时的,所以为了解决这个问题,本文提出一种可以自动标注标签的半监督学习方法.该方法主要利用弱分类器对未知标签的数据进行类别标定,然后结合模糊度[13]这一指标选择不确定性小的数据来扩充原有的有标签的数据集.

在 Bug报告分类中,第 3个问题是:数据集的样本总量不充足.在训练分类器时,往往需要充足的训练数据.当训练数据不充分时,会导致训练得到的分类器出现严重的过拟合现象.过拟合现象主要表现为:分类器在训练集上的分类效果良好,可是在测试时或者在实际工作中,其分类效果很不理想.这主要是因为训练样本容量少导致分类器对数据的统计规律学习得不充分,最终使其泛化能力弱,不能对训练集以外的数据做出正确的判别.

为了解决这个问题,我们提出一种样本迁移[14]的方法,即用其他 Bug数据集里的样本来补充数据量不充足的数据集的样本容量.自然地,如何选取样本来补充数据集,这是一个十分关键的问题.在我们的工作中,我们仍旧利用第二个问题里的方法.即先在原数据集上训练得到一个弱分类器,然后用弱分类器对被迁移的样本进行分类,得到分类结果后,结合模糊度,选择模糊度小的样本来补充原始的数据集.在这个过程中,需要注意,不同的数据集的样本维度可能不同.为了统一维度,我们提出使用受限玻尔兹曼机(restricted Boltzmann machines,简称RBM)[15]来对不同数据集的样本进行编码,即将不同数据集里的样本编码成统一维度的数据.这样做使得我们的方法具有更加广泛的适用性.注意到,用来自不同分布的样例来补充训练集合,这个方法的可行性已经在文献[16]得到证明,并且在我们的实验中会进一步被验证.

综上所述,本文的贡献点主要有 3个方面:(1) 针对Bug报告中的类别不平衡问题,我们将基于代价的分类器训练方法引入到Bug报告分类问题里,并且使用ELM作为基本的分类模型;(2) 针对Bug报告中被标记的样本数量不充足的问题,我们将基于模糊度的半监督方法引入到 Bug报告分类问题里,通过扩充有标签的样本容量来增强分类效果;(3) 针对Bug报告中数据集样本总量不充足的问题,我们将基于RBM和模糊度的样本迁移方法引入到Bug报告分类问题里,通过扩充训练集总样本容量来避免分类器出现过拟合的现象.

本文第1节介绍本文涉及到的相关背景知识.第2节详细介绍本文提出来的方法.第3节展示本文的相关实验.第4节对本文的工作进行总结与展望.

1 背景知识

在这一节中,我们将详细介绍本文主体方法所涉及到的背景知识.这些背景知识主要分为两个部分:第 1个是ELM的训练策略;第2个是RBM的学习方法.

本文主要关注的是对 Bug报告数据集的分类问题.我们选用的是基于神经网络的分类器.神经网络是一种非线性的函数模型,该模型通过调节网络参数,可以拟合输入到输出的映射关系.近几年,神经网络在模式识别领域里取得了很多令人瞩目的成果[17-19],尤其在自然语言处理的工作里,基于神经网络的方法要明显优于其他方法的效果[20].自动识别Bug报告的类别,是一种关于自然语言的类别识别工作,所以我们选用神经网络作为分类模型.

按照训练方式划分,神经网络可以被分为两种类型:第1种是基于迭代优化的方法[21]来调整网络的参数;第2种是基于随机赋权的方法[22,23]来学习网络的参数.其中,ELM作为一种随机赋权网络模型,在近几年广泛受到关注.ELM主要的优点是训练方式高效快捷,并且在大多数领域里,其性能要优于或者等于迭代寻优算法训练出来的网络.接下来,我们详细介绍ELM的参数学习过程.

ELM模型是一个单隐层的前馈神经网络,如图1所示.其中,I是网络的输入层(由nus个节点组成),H是网络的隐层(由ncc个节点组成),O是网络的输出层(由ns个节点组成).输入层和隐层之间的权重α∈ℝnus×ncc是网络输入层权重,隐层和输出层之间的权重β∈ℝncc×ns是网络的输出层权重,为了增加网络模型的线性表达能力,在隐层加入了偏置矩阵B=[b1,b2,…,bn]T,其中,bi=(b1,…,bncc)T.为了提高网络的非线性表达能力,隐层的每一个单元节点需要被非线性函数作用,这里称这个函数为激活函数,一般地,该函数选择的是sigmoid函数,即

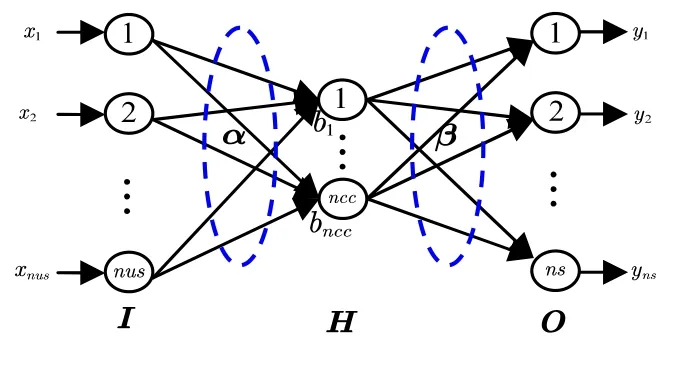
Fig.1 Feedforward neural network model with single hidden layer图1 单隐层前馈神经网络模型

ELM的训练方法是有监督的方法,因而在训练过程中需要有标签的数据集S.在S中,条件属性矩阵用X表示,决策属性矩阵用T表示,这两个矩阵的形式如下所示.

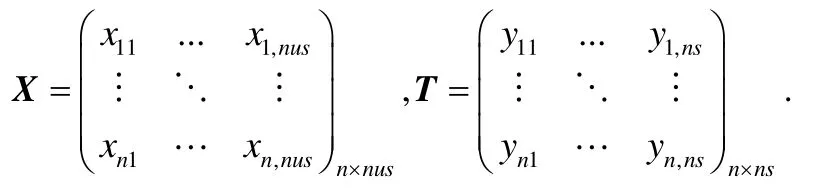
其中,n代表数据集S中的样本总个数;X中每一行是一个nus维的样本向量;T中每一行是一个ns维的标签向量,该向量用one-hot形式表示,且ns等于数据集里的类别个数.

在实际的分类工作中,I接收输入矩阵X,经前向传播依次得到H的输出H∈ℝn×ncc和O的输出Y∈ℝn×ns.

其中,X是已知的,α和B是被随机赋值的,只有β一个是未知量,也就是需要优化求解的网络参数.优化的目标是最小化网络输出Y和期望输出T之间的距离:

β可以用下面的等式求解.

很明显,通过上式求解β是一个最小二乘问题.其中,为了更一般化地定义上式的求解过程,可以求H的广义逆,即Moore-Penrose逆.

接下来将介绍本文所涉及到的另一个数学模型,即RBM.RBM是一个概率图模型[24],其结构如图2所示.可以看出,RBM是一个无向二分图模型.其中,v=(v1,v2,...,vnv)是可见层(由nv个节点构成),h=(h1,h2,...,hnh)是隐藏层(由nh个节点构成).RBM在本文里的主要作用是将可见层的数据编码成隐藏层的表达形式.由于RBM的训练机制采用的是无监督的方法,所以训练数据集S={v1,v2,…,vN}里的样本vi不需要标签属性,N是样本个数.

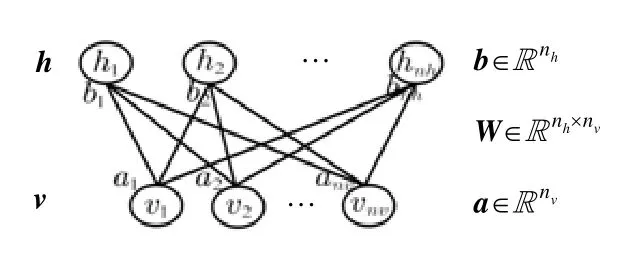
Fig.2 Network structure of RBM图2 RBM网络结构

可见层和隐藏层的条件概率公式可由下面的公式来表达.

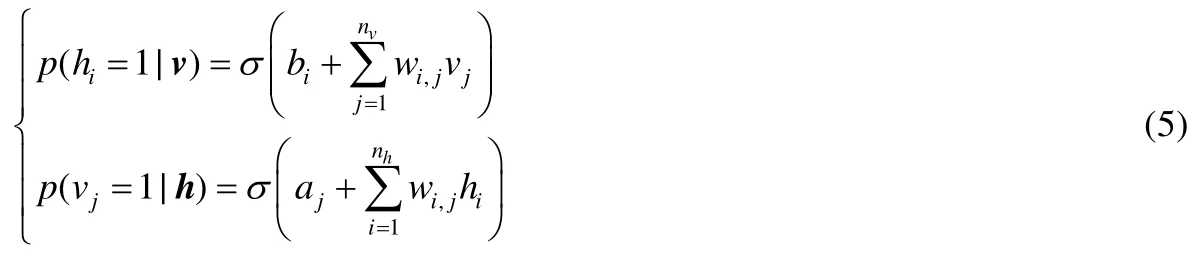
其中,σ的函数形式是 sigmoid函数.在上面的式子中,a=(a1,a2,...,anv)是可见层偏置,b=(b1,b2,...,bnh)是隐藏层偏置,W=[wi,j]nh×nv是RBM的网络权重.a,b和W是需要学习的参数θ.给定训练集合S,优化目标是求解下式的极大似然.

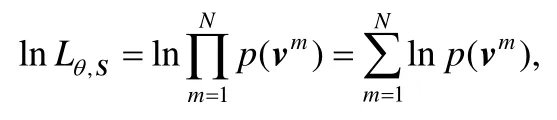
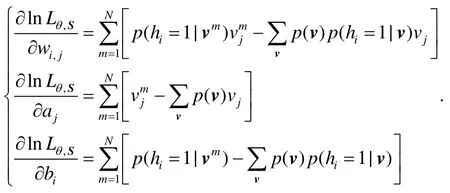
可以看出,因为∑v的存在,上式的计算复杂度为O(2nv+nh).为了简化计算复杂度,可以采用 Gibbs采样[24]的方法,经过t次采样后,上式可以通过下面的式子近似求解.

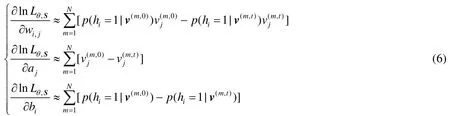
具体地,在本文里,我们采用Hinton等人[25]提出来的对比散度(contrastive divergence,简称 CD)算法来优化RBM模型的参数,优化过程如算法1所示.

算法1.RBM的训练算法.

2 方法设计

在这一节中,我们将详细介绍我们提出来的方法,并且将这个新的方法用于解决 Bug报告分类中普遍存在的3个问题:第1个问题是数据类别不平衡问题,第2个是训练集里被标记的数据不充足的问题,第3个是数据集之间的样本迁移问题.

2.1 基于代价ELM解决数据不平衡问题

ELM 是一种随机赋权网络模型,和其他神经网络一样,是一种非线性函数.在分类问题里,ELM 将条件属性域里的样本映射为决策属性域里的类别标签.在这一点上,ELM和其他分类器一样,都是通过学习样例到标签之间的映射关系来进行分类工作.ELM的具体学习过程在第1节里已经详细介绍,这个学习过程的优化目标就是最小化实际输出和期望输出之间的距离,这个距离通常是二者之间的欧氏距离.在分类问题中,网络的期望输出是样例的类别标签(一般将其表达成 one-hot形式的向量),通过最小化网络的实际输出向量与期望输出向量之间的欧氏距离,来学习得到网络的参数.

可是,有一个问题需要注意:在分类问题里,每一类的样例被错误分类的代价应该是不同的,比如在不平衡数据集里,多数类样例因为样本个数多,所以更容易被正确分类,而少数类样例则更容易被错误分类,所以一个多数类样例被错误分类的代价应该小于一个少数类样例被错误分类的代价.但是在ELM以及大多数分类器的前提假设里,都默认每个类别的样例被错误分类的代价是一样的.

本文主要是解决Bug报告的严重性分类问题.在实际工作中,严重的Bug需要被即时处理,不严重的Bug可以被延时处理.在自动分类Bug时,就需要准确预测Bug报告的严重程度,将严重的Bug识别出来,即时地提交开发人员处理.但是在大多数Bug报告数据集里,严重的Bug样例个数要明显多于不严重的Bug样例个数,因此Bug报告数据集通常都是类别不平衡的数据集.这样导致分类器易将不严重Bug误报成严重Bug,降低了分类器对严重 Bug的识别准确率.为此,我们对 ELM 模型在分类问题上进行扩展,得到一种考虑到错误代价的分类模型.因此,我们引入代价敏感的ELM分类模型[26].

为了构建代价敏感的ELM分类模型,首先需要构造一个错误分类的代价矩阵D,即

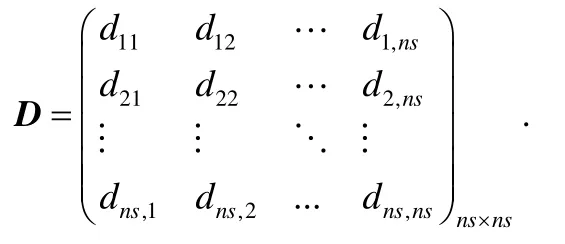
在这个矩阵里,di,j代表第i类样例被错误分到第j类的代价大小,很明显地,di,j等于零,也就是第i类样例被正确分类时所产生的代价是零.我们用ci代表第i类样例被错误分类的代价,ci可以用下面的公式求得.

假设数据集里的类别个数一共是ns,那么通过等式(7),所有类别的样例被错误分类的代价可以被集合Cost表示:Cost=(c1,c2,…,cns).

通过引入代价矩阵,代价敏感的ELM将原始的ELM扩展成了一个考虑到错误分类代价的分类模型.在优化过程中,代价敏感的 ELM 将优化目标扩展成为一个带有代价权重的欧氏距离之和.为了表示这个优化目标,首先将训练集里的样例按照类别分组,同上,这里假设类别个数为ns,每一组样例同属于一个类别,这个组可以被表示为Xi,被分组后的数据集可以被表示为可以由下面的公式求出.,其对应的标签矩阵为T,对应的隐层矩阵H

代价敏感的ELM的优化目标是最小化分类错误代价,通过上面给出的一些符号化定义,这个优化目标可以被表示为

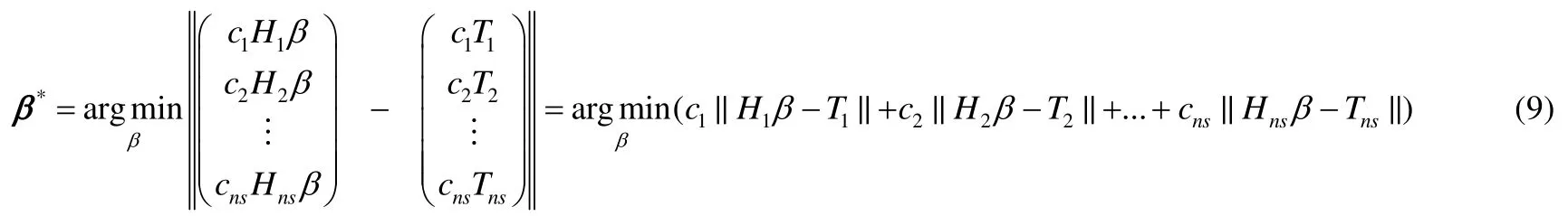
和第1节介绍的ELM参数优化求解方法一样,这里的矩阵求逆可通过Moore-Penrose广义逆来求解得到.

在本文所要解决的Bug报告分类问题中,数据集都是二分类问题,其中多数类是严重的Bug报告,少数类是不严重的Bug报告.通常,这两类之间会存在很大的不平衡度[9,10],因此,我们在这里提出来用代价敏感的ELM来分类 Bug报告数据集里的样例,通过给少数类样例比较大的错误分类代价,给多数类样例比较小的错误分类代价,并且最小化错误分类的总代价,来自动地解决Bug报告数据集在分类过程里存在的类别不平衡问题.

其中,所有数据集上的代价矩阵是一个 2×2的方阵,对角线上元素全为 0,代表着样例被正确分类的代价是0,其他元素则分别代表着少数类样例被错分类到多数类的错误代价ca和多数类样例被错分到少数类的错误代价cb.在设置代价矩阵时,ca要大于cb.之后,通过最小化错误分类的总代价,可以使ELM模型对少数类的错误分类更加敏感,从而达到解决分类中的类别不平衡问题.用代价敏感的ELM来解决Bug报告分类中不平衡问题的过程可以用算法2来表示.

算法2.代价敏感的ELM的训练算法.

(1) 输入:条件属性矩阵X,标签属性矩阵T//输入的矩阵已按类别分组

(2) 初始化:隐层节点数ncc,代价矩阵D;随机初始化:输入权重α,隐层偏置B

(3) 用公式(8)计算隐层输出值矩阵H

(4) 通过公式(10)求解β*

(5) 返回β*

2.2 基于半监督方法处理训练数据不充分问题

本文之前介绍的ELM方法和代价敏感的ELM方法都是有监督学习的方法,监督学习的方法需要训练数据既有条件属性也要有与之相对应的标签属性.但是在软件测试的过程中,条件属性容易获得,与之对应的标签属性则需要精密的人工标注才可以获得.面对这种情况,我们在本节提出一种基于模糊度的半监督学习方法[26],并且用这种方法来解决软件 Bug报告的分类问题.在文献[26]里已经证明,高模糊性的样例的分类代价要明显大于低模糊性的样例的分类代价,所以这里使用低模糊性的样例来填充原数据集可以避免整体的分类代价过高,而且 Wang等人[13]提出,模糊性与不确定性存在着正相关的关系,低模糊性的样例具有低的不确定性,也就是被正确分类的可能性较大,这也是我们选择低模糊性样例来填充数据集的原因.

如上所述,在软件测试过程中会产生很多无标签的数据,而软件 Bug报告分类问题主要就是通过学习条件属性到标签数据之间的映射关系,使得分类器可以自动分类这些数据.目前,在机器学习领域都是使用数据驱动的分类方法,这就需要在训练这些分类器时,可以提供大量的有标签的训练数据.本文里,这些数据的标签只有严重和非严重两类.但是要想获取这些标签,就需要大量的人工标注.人工标注的工作往往耗时而且代价昂贵,这就很自然地使人们想到用未标注的数据来解决软件测试Bug报告的分类问题.

在利用未标注的软件测试 Bug报告数据时,我们提出了一个方法,即通过在有限的有标注的数据集上训练出一个弱分类器,然后用这个弱分类器对未标注的数据进行分类,得到分类结果后,我们通过模糊度来衡量这些分类结果的可信程度,选择可信程度高的数据来补充原始的训练数据集,而这些数据的标签属性则是通过弱分类器给出.

理论上,上述过程可以重复多次,每一次都从未标注的数据集里挑选出可信程度大的数据来补充训练数据集.因为训练数据集的样本容量在不断地扩充,所以训练出来的分类器的分类性能也会逐渐提高.最终的理想结果是,未标注的样例全部被自动地加上标签并且被扩充到训练集里.通过这个完备的数据集,可以训练得到一个泛化能力很强的分类器.但是需要注意:当分类器的分类精度不是很高时,错误分类的情况很可能会发生,也就是未标注的样例在这种情况下很可能被标上错误的标签,这样就会干扰分类器性能的提升.因而,要想达到之前所述的理想的情况,每次选择多少未标注的样本来扩充训练集,这是一个很关键的问题.

在实现这个方法的过程中,最关键的指标是未标注数据的模糊度的测量.模糊度的计算有多种方法,Zadeh等人[27]总结出了一些计算模糊度的方法,其中包括基于Hamming距离或者欧式距离的模糊性的计算方法、针对大型多类问题的模糊性计算方法.在本文中,我们利用下面的方法来计算模糊度的大小.

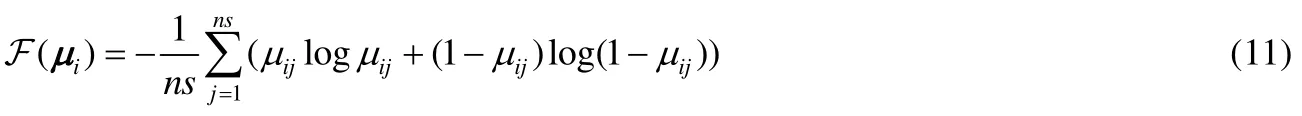
其中,向量μi=(μi1,μi2,…,μi,ns),μij是第i个样本属于第j类的隶属度大小.

因为考虑到了数据集里类别不平衡的因素,所以在实现本节的方法时,分类器采用的是代价敏感的ELM模型.但是注意到,在计算模糊度时,需要知道样例属于每一个类别的后验概率.可是在ELM的原始设计中,网络输出的值Y=[yij]n×ns不能表达这个信息.基于此,我们引入了softmax,将该函数作为激活函数作用到网络的输出层,计算公式如下所示.

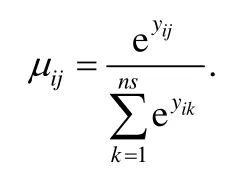
算法3详细表达了上述的基于模糊度的半监督方法.

算法3.半监督训练算法.

(1) 输入:有标签的条件属性矩阵X,标签属性矩阵T;无标签的条件属性矩阵Z

(2) 初始化:隐层节点个数ncc,代价矩阵D;随机初始化ELM的输入层权重和隐层偏置

(3) 根据算法2,利用数据X和T训练一个代价敏感的ELM:CELM

(4) 利用CELM对样本矩阵Z进行分类

(5) 得到Z上的分类结果后,通过公式11计算每个样本的模糊度

(6) 对模糊度进行升序排列,选择前k个样例zx补充数据集X,

用zx被CELM分类得到的标签zy补充T

(7) 在补充后的数据集上重新根据算法2训练代价敏感的分类器

(8) 返回新得到的分类器的参数矩阵β

2.3 Bug报告数据集间的样例迁移方法

第 2.2节介绍了一种基于模糊度的半监督方法,这个方法主要为了解决训练数据中标注样本少的问题.这个方法的提出是基于一个假设,即未标注的样本和少量的有标注的样本来自同一个数据集.但是在软件测试Bug报告的数据集里,不仅被标注的样本量少,而且整体的样本总量也很少.在训练分类器时,训练数据集的样本量不充足会带来的问题是使得训练得到的分类器容易过拟合,也就是该分类器在训练集上表现良好,可是其泛化能力很弱.在实际工作中,泛化能力弱的分类器在处理新的待分类样本时,往往会给出错误的决策.

为了解决 Bug报告中有些数据集的样本总量过少的问题,我们在本节提出一种基于模糊度的样例迁移方法.该方法不需要被迁移的样例与已有样例来自同一数据集,即为了扩充训练集的样本容量,可以使用该方法将别的数据集里的样例迁移到训练集里来扩充样本容量.

该方法的好处就是可以解决因为样本容量少而导致的过拟合问题,但是在选择样例上,该方法存在着和上一节一样的问题:如果样本选择不好,则同样会导致过拟合的问题出现.为了更加客观地选择样本,我们先在已有的数据集上训练得到一个弱分类器,然后用该分类器对被迁移数据集进行分类,得到分类结果后,可以计算每个样例的模糊度,模糊度越大,不确定性越大,所以选择模糊度小的样例来补充原有的数据集,这些样例的标签通过弱分类器得到.然后,在扩展后的数据集上再次训练分类器.这个过程可以一直重复,直到得到合适的训练样本容量.

需要注意的是,为了避免数据集里类别不平衡问题的干扰,在这个方法里,我们选择的分类器同样是代价敏感的 ELM 模型.在实际工作中,另一个需要解决的问题是不同数据集的样本维度通常不一样,这个问题限制了这个方法的应用范围.为了解决这个问题,使得我们的方法更具一般性,我们将RBM引入到该方法中.

在第1节里已经介绍了RBM.RBM可以被视为一种样本编码工具,即可以通过非线性变换,将样本从一个维度空间映射到另一个维度空间.在编码的过程中,RBM 保证编码前和编码后的样本是等价的.在本节的工作里,我们采用RBM将不同数据集里的样本编码成统一的维度,这样就为分类器在不同数据集上进行迁移训练提供了可能性.我们用S={X,T}表示原数据集;同时,用St表示被迁移数据集St={Xt}.基于这些符号化的定义,该节提出来的方法可以用算法4来详细表述.

算法4.样本迁移算法.

(1)输入:数据集S,其中,条件属性矩阵X,标签属性矩阵T,被迁移的数据集St={Xt}

(2)初始化:ELM的隐层节点个数ncc,代价矩阵D,RBM的隐层节点个数nh.

随机初始化:ELM的输入层权重和隐层偏置

(3)通过算法1,利用数据X和Xt分别训练得到两个RBM模型

(4)通过训练得到的RBM对X和Xt进行编码,得到新的数据表达形式Xp和Xtp

(5)根据算法2,利用数据Xp和T,训练得到一个代价敏感的ELM:CELM

(6)利用CELM对数据集Xtp里的样本进行分类

(7)得到Xtp上的分类结果后,通过公式(11)计算每个样本的模糊度

(8)对模糊度进行升序排列,选择前k个样例trx补充数据集Xp,

用trx被CELM分类得到的标签try补充T

(9)在补充后的数据集上重新根据算法2训练代价敏感的分类器

(10) 返回新得到的分类器的参数矩阵β

3 本文实验

本文针对软件测试Bug报告数据集里存在的3个问题提出了3个解决方法,即针对训练数据集类别不平衡问题,提出了代价敏感的 ELM 分类方法;针对数据集被标记的样本较少的问题,提出了基于模糊度的半监督方法;针对训练数据集总体样本量较少的问题,提出了基于模糊度和 RBM 的样本迁移方法.为了验证我们提出的方法的有效性,我们开展了3组验证性的实验.

在本节中,实验所采用的数据集是真实的软件测试Bug数据集.数据集来自3个开源项目.本节实验里用到的数据集一共21个,其中,7个Eclipse[28]、7个Moizlla[29]、7个GNOME[30].数据集的名称以及数据集的不平衡度都在表1～表3中被列出.其中,不平衡度Imbalance Ratio(IR)的计算如下所示.

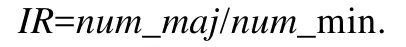
其中,num_min是少数类的样本个数,num_maj是多数类的样本个数.

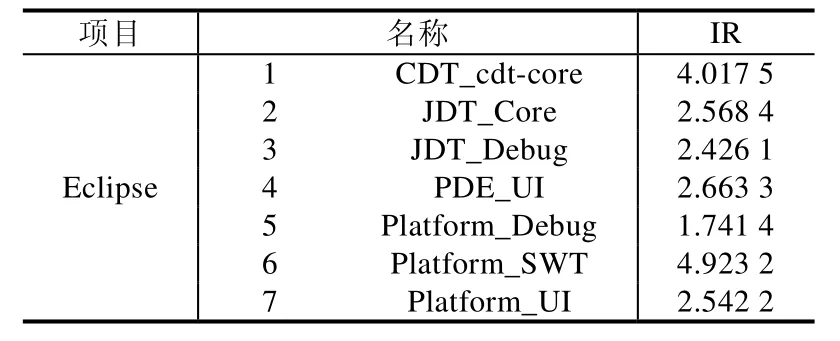
Table 1 Datasets of Eclipse Bug reports表1 Eclipse Bug报告数据集

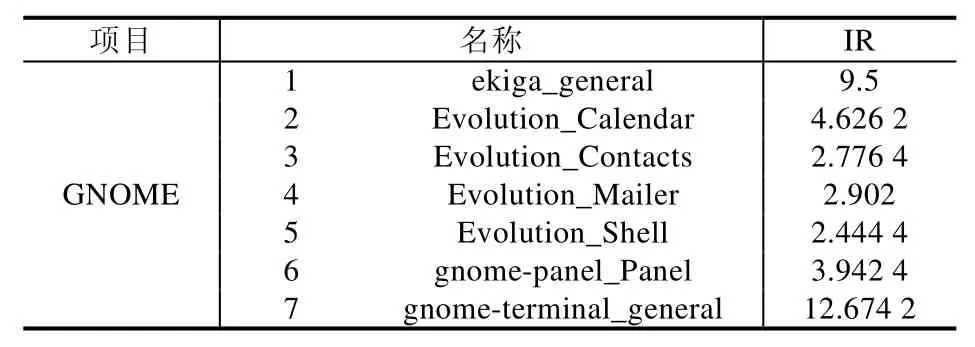
Table 2 Datasets of GNOME Bug reports表2 GNOME Bug报告数据集

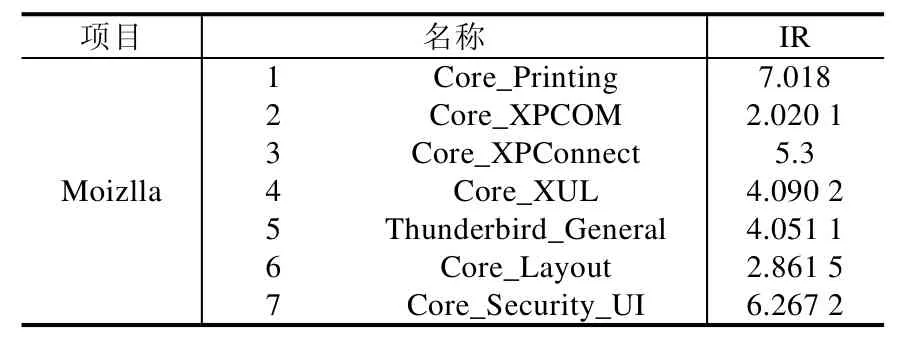
Table 3 Datasets of Moizlla Bug reports表3 Moizlla Bug报告数据集

在接下来的实验里,我们采用的评价指标分别是准确率和加权的F-measure[31].其中,准确率是样本被正确分类的比率;加权的F-measure是两类样例在查全率和查准率上的一个综合性的指标,在本文实验里,该指标更能反映出分类器对严重Bug的误报程度.准确率的计算如下所示:

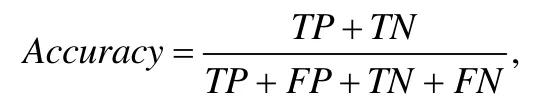
其中,Accuracy是准确率,TP、FP、TN和FN的关系可以用表4表示.

Table 4 Confusion matrix表4 混淆矩阵

F-measure的计算如下:

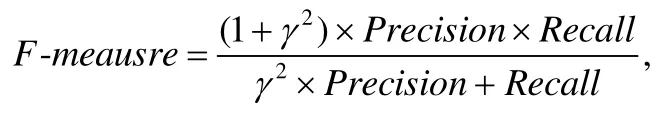
其中,在本文实验里,γ等于1,Precision代表查准率,Recall代表查全率,这两个指标的计算可由下面的公式表达.

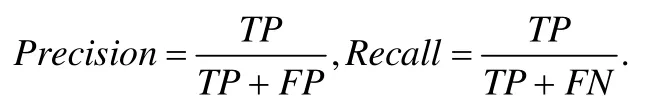
本文所用到的加权F-measure计算如下:

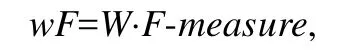
其中,wF是加权的F-measure;W=(w1,w2),w1是第1类样例占的比例,w2是第2类样例占的比例.

本节的第 1个实验是验证代价敏感的 ELM在不平衡数据集上的分类效果.作为对比,我们用传统的 ELM在相同的数据集上进行实验.除此之外,我们还比较了基本的分类器,即朴素贝叶斯模型(NB)、BP神经网络模型(BPNN)和支持向量机(SVM)[32].数据集的划分是:把数据集平均分成5份,每次随机取3份作为训练集,剩下的2份作为测试集.为了保证客观性,我们对两个方法都进行了100次实验,最后的结果是取这100次实验的平均值.在每次实验里,为了保证公平性,代价敏感的ELM和传统的ELM的隐层节点数以及BPNN的隐层节点数都被设置成一样的个数,并且两个模型的输入层权重和隐层偏置也都被相同的随机数赋值.我们在实验里给权重和偏置随机赋权的方法是在区间[0,1]里随机取值.表5～表10给出了这组实验的对比结果.

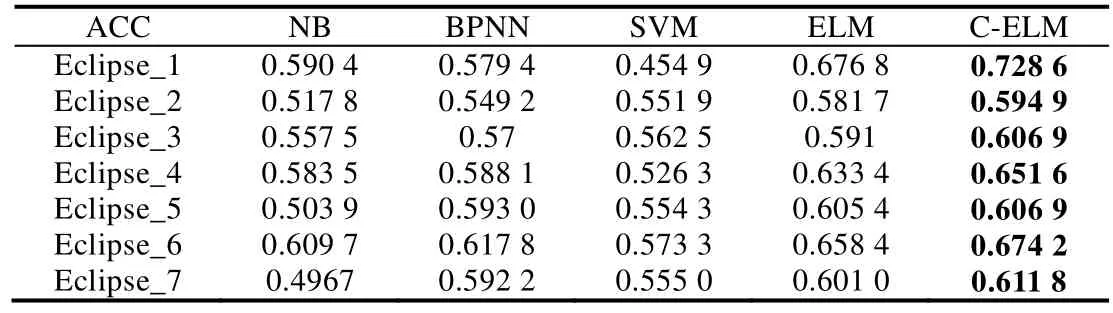
Table 5 Testing accuracies on Eclipse datasets表5 Eclipse数据集上的测试准确率

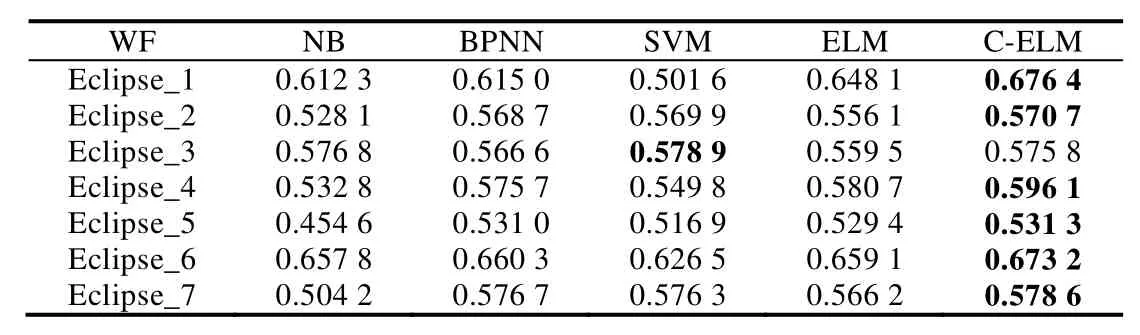
Table 6 WeightedF-measures on Eclipse datasets表6 Eclipse数据集上的加权F-measures

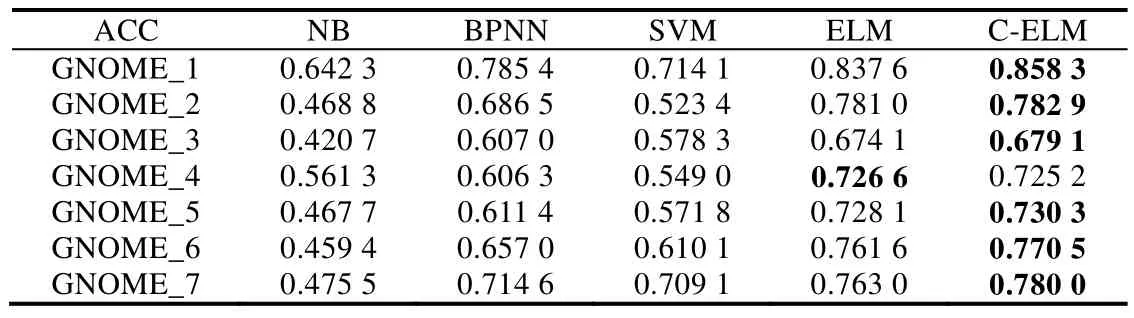
Table 7 Testing accuracies on GNOME datasets表7 GNOME数据集上的测试准确率

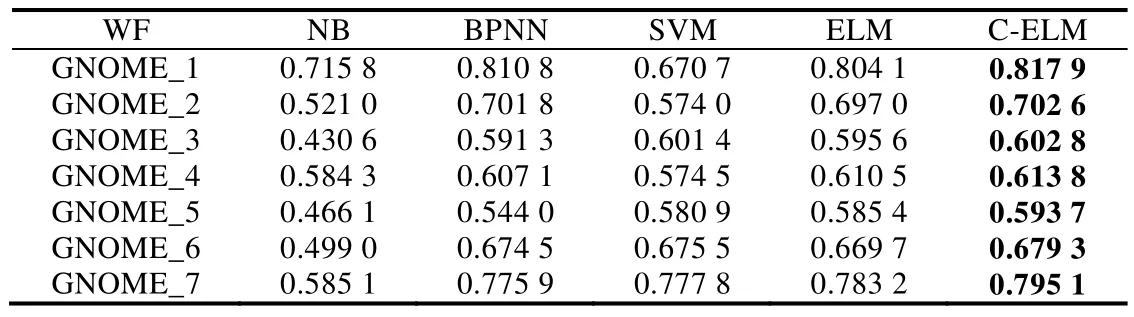
Table 8 WeightedF-measures on GNOME datasets表8 GNOME数据集上的加权F-measures

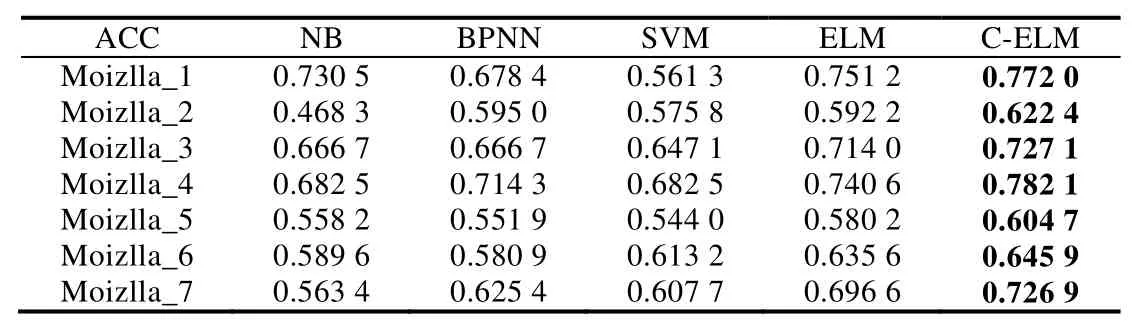
Table 9 Testing accuracies on Moizlla datasets表9 Moizlla数据集上的测试准确率

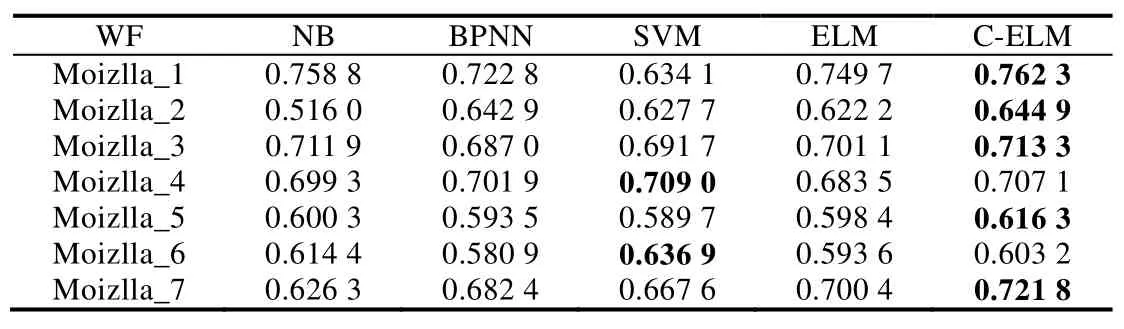
Table 10 WeightedF-measures on Moizlla datasets表10 Moizlla数据集上的加权F-measures

通过表1～表3的最后一列可以看出,Bug报告数据集都是有着不平衡度的数据集,而且有些数据集的不平衡度较大.在处理数据类别不平衡这个问题时,通过给少数类样例更大的错误分类代价,得到的分类准确率在绝大多数 Bug报告数据集上有了很明显的提升.虽然在表7中,GNOME_Evolution_Mailer的准确率结果要偏低,但是通过加权的F-measure值的比较可以看出,代价敏感的分类器在重要数据样本的分类上面表现仍旧良好,也就是对严重Bug的误报率较低.而且通过在所有数据集上比较加权的F-measure值可以看到,基于代价的分类模型都能取得很好的效果.与其他传统的分类器相比,ELM 方法需要设定的参数更少,尤其与 BPNN的比较中,ELM的训练时间要远远低于BP迭代调参所需要的时间,并且在绝大多数数据集上,ELM方法可以取得较好的效果.在图3中,我们比较了欠采样方法(RUS-ELM)、过采样方法(ROS-ELM)、合成过采样方法(SMOTE)与代价敏感方法.欠采样方法是对多数类样例进行随机删减,可以看出,因为减少了训练样本的容量,并且在删减样本的过程中容易丢失重要数据,所以该方法效果不是很好;过采样的方法则是对少数类样例进行扩充,该方法可能会受到冗余数据的影响,造成分类器过拟合,对分类器泛化能力造成不好的影响;SMOTE方法相对表现较好,但是该方法容易造成类间的 overlapping现象,且在类别临界面生成样例时,容易将合成的多数类样例标记成少数类类别,从而不利于分类器对数据分布特点的学习.通过比较,基于代价敏感的平衡方法在绝大部分数据集上都有较好的结果,而且基于代价的方法表现得更加稳定,更适合被用于实际的工作中.从效率上来看,基于代价的方法不需要事先对数据集进行平衡化的预处理,而是可以进行端到端的训练,从而更加满足本文研究领域的需求.

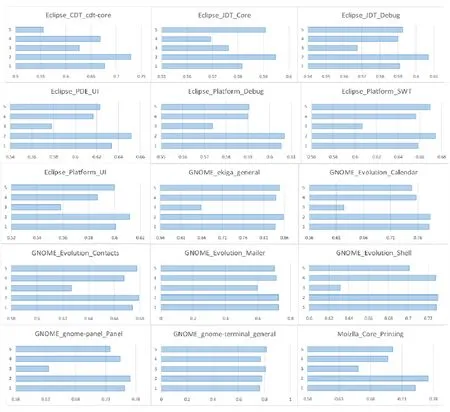
Fig.3 Comparison among RUS,ROS,SMOTE and cost-based method图3 欠采样、过采样、合成过采样和代价敏感方法的比较

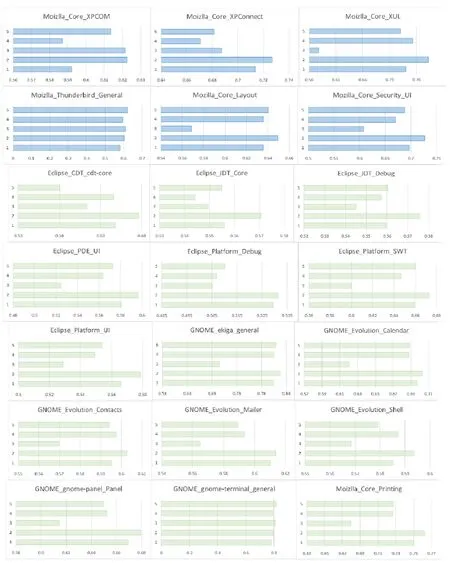
Fig.3 Comparison among RUS,ROS,SMOTE and cost based method (Continued 1)图3 欠采样、过采样、合成过采样和代价敏感方法的比较(续1)

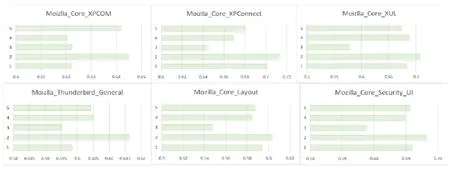
Fig.3 Comparison among RUS,ROS,SMOTE and cost based method (Continued 2)图3 欠采样、过采样、合成过采样和代价敏感方法的比较(续2)

图3中的结果都是实验重复100次得到的平均值,蓝色图是准确度的结果,绿色图是加权F-measure值的结果.1～5分别代表ELM、CELM、RUS-ELM、ROS-ELM和SMOTE-ELM.

本节的第 2个实验是验证基于模糊度的半监督方法在扩充训练集样本容量上的有效性.在这个实验里,我们采用的分类器是代价敏感的 ELM 模型,目的是为了避免数据集里不平衡问题的干扰.在该实验里,对原始数据集的划分是:将数据集划分成6份,每次随机选择其中的3份作为训练集,在剩下的数据中,随机选择2份作为测试集,最后留下的数据作为验证集.其中,验证集则是本文第2.2节里提到的未标注数据集.在实验过程中,我们先在原始的训练集上训练得到一个弱分类器,然后在验证集上对样例进行分类,之后通过模糊度的大小选择一定数量的验证集样例来扩充原始的训练集,然后用扩充得到的数据集再次训练一个分类器.为了保证客观性,前后两个分类器的各项参数的设置完全一样,具体操作方法如第 1个实验所述.为了通过对比显示我们方法的有效性,我们用两次训练得到的分类器对测试集的样本进行分类,最后通过上述两个指标来评价分类结果,该结果同样是对100次的实验结果求平均值得到的最终结果.我们用First表示在原始数据集上训练得到的分类器的测试结果,用Second表示用扩充后的数据集训练的分类器的测试结果.这部分的实验见表11.

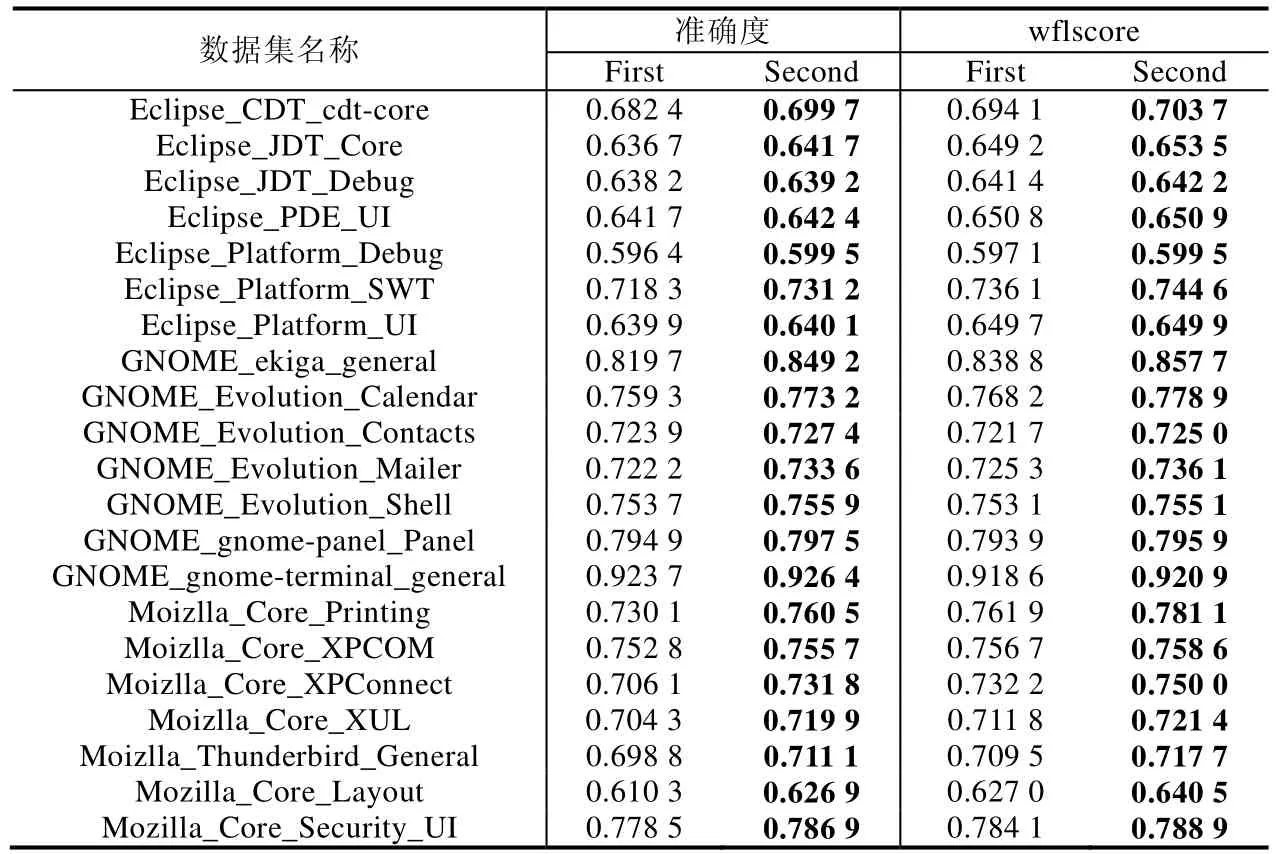
Table 11 Experimental results of semi-supervised approach表11 半监督方法的实验结果

从表11可以看出,通过基于模糊度的半监督方法来扩充数据集,并且用新的数据集再次训练分类器,所得到的分类器的分类效果在每个数据集上都有了提升.这证明了我们提出来的这个方法对于改善分类器的泛化能力是有效的.

本节的第3个实验是验证基于模糊度和RBM的样本迁移方法的有效性.在这个实验里,我们采用的分类器同样是代价敏感的ELM模型.我们对原始数据集的划分方法和第1个实验里数据集划分方法一样.对于被迁移的数据集,我们没有采用任何的划分方法.在进行分类之前,我们首先对原始数据集的整体进行 RBM 编码,同时对被迁移的数据集的整体进行RBM编码.在这两次编码中,我们采用3个级联的RBM对输入数据进行维度空间的变换.在编码过程中,我们只需要保证两次编码的输出维度一样即可,中间隐层的维度则可以自主调节.分类实验的具体操作过程是,先在原始的训练集上训练得到一个分类器,然后对被迁移的样本进行分类,用分类结果计算每个样本的模糊度大小,根据模糊度大小来选择样本来扩充原始的训练集.之后,再利用扩充后的训练集重新训练一个分类器.在实验过程中,前后两个分类器的参数设置完全一样.为了体现实验的客观性,我们重复本实验的全部过程(编码过程和分类过程)100次,最后取这100次的平均值作为实验结果.我们用Before表示在原始数据集上训练得到的分类器的测试结果,用After表示在被扩充后的数据集上训练得到的分类器的测试结果.这些结果展示在表12中.

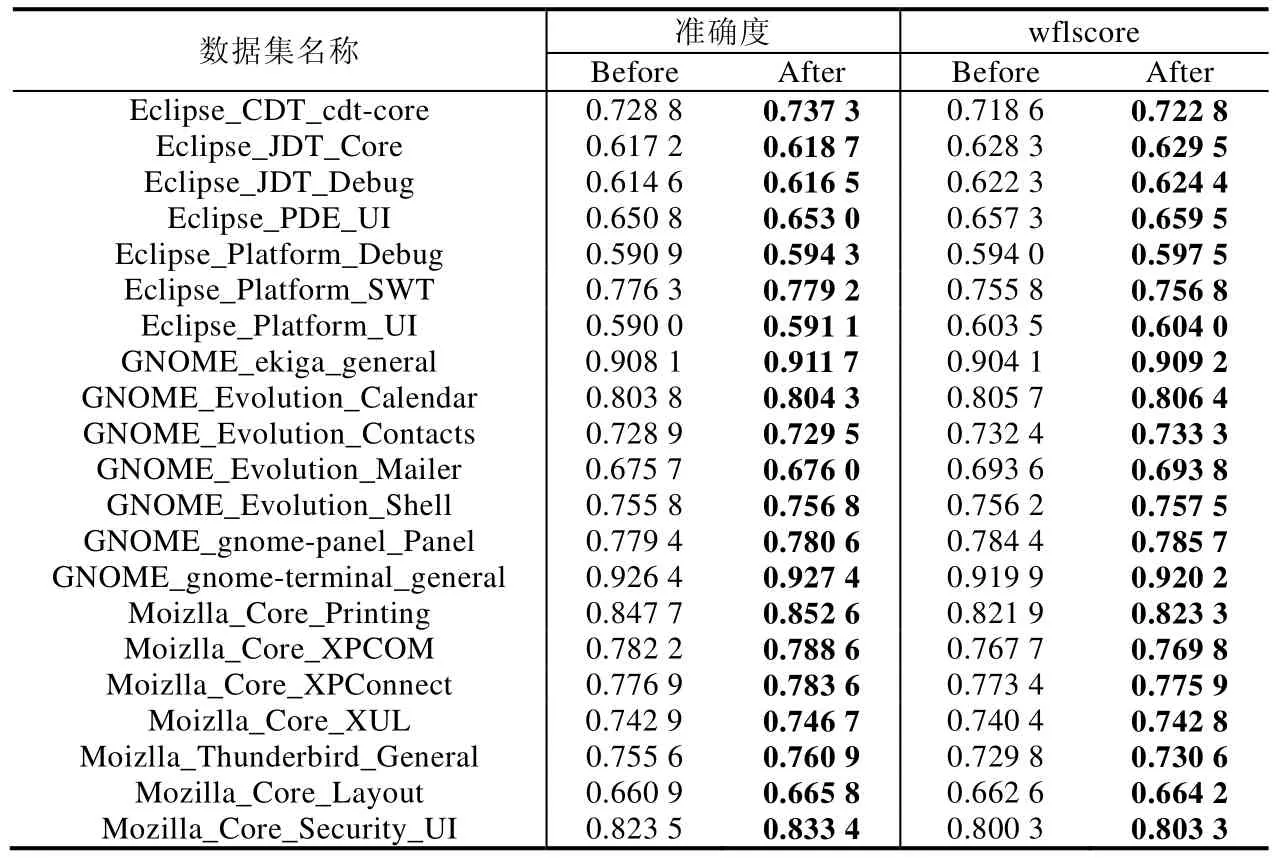
Table 12 Experimental results of transferring approach表12 迁移方法的实验结果

从表12中我们可以看出,无论是准确率还是加权的F-measure值,再次训练的分类器都取得了较好的效果.这个结果显示,基于RBM和模糊度的样本迁移方法在扩充样本容量并且提升分类器的泛化能力这些方面是有效的.

本节的实验基本验证了我们提出方法的可行性和有效性.其中,如第 3节所述,在利用半监督方法扩充训练集时,理论上可以进行多次迭代,逐渐扩充训练集的样本容量.在之前的实验里,我们设置的迭代次数为两次,即对分类器进行再训练的优化策略.再训练的结果已经表明,我们的方法是有效的.为了进一步验证我们的方法在数据集样本量继续扩充的条件下仍旧是有效的,我们将迭代次数增加,图4显示了随着迭代次数增加,我们的方法在每个数据集上的表现.

在上面的实验中,为了保证客观性,我们将实验重复了 100次,然后取平均值.在每一次的实验中,我们提前将数据集按照3:2:1的比例分别分成训练集、测试集和验证集.其中，验证集是用来扩充训练集样本容量的数据集合.然后,我们利用半监督方法逐步地对训练数据集扩充了5次,每一次扩充后都在测试集上进行测试,并给出上图所示的测试结果.值得注意的是,为了克服随机赋权的影响,5次迭代中,分类器的随机参数都是相同的值,实验结果就只会受到数据集样本容量变化的影响.从图4可以看出,在利用本文的半监督方法的前提下,随着数据集样本容量的增加,分类器的性能也在逐步提升,这一现象在 21个数据集上都有体现.通过这组实验,验证了我们提出来的方法的有效性,即在人工标记的数据不充足的条件下,可以利用有效的半监督机制[33,34]来逐步扩充训练样本集,最终可以达到提升分类性能的目的.

Fig.4 Results of five tests on 21 datasets图4 21个数据集5次测试的结果

本节实验里,网络结构参数、代价矩阵的设置以及其他参数的具体情况,都详细地列在了本文的附录里.

4 总 结

本文主要解决软件测试Bug报告中的样例分类问题.在实际工作中,我们发现Bug报告数据集普遍存在着3个问题:第1个是样本类别不平衡问题,第2个是数据集里被标注的样本个数不充足的问题,第3个是数据集的样本总容量不充足的问题.这3个问题都会对分类工作产生不良的影响.为了解决这3个问题,我们提出了3种方法:第1种是基于代价敏感的ELM模型来增加少数类样例被错误分类的代价,从而解决类别不平衡问题带来的影响;第2种是基于模糊度的半监督方法来自动标注没有标签的数据,从而扩充有标签的数据集;第3种是基于RBM和模糊度的样本迁移方法来扩增原有数据集的方法.本文通过几个实验验证了我们提出的方法是有效的、可行的.最后,可以注意到,本文提出来的方法具有很好的扩展性,可以与不同的模型[35-38]相结合.本文未来的研究工作将与集成学习[39,40]的方法相结合,以进一步提升目前的方法在 Bug报告分类问题上的效果,同时将结合后的方法应用于更多的相关领域[41-43].

附录

证明:用softmax的输出来表示后验概率的合理性.

定义x(1),…,x(m)为m个输入向量,且x(i)∈ℝ1×ncc,ncc为输入向量的维度,x(i)j是向量x(i)第j维属性值,i=1,2,…,m,j=1,2,…,ncc.对ELM的输出层来讲,其输入向量x(i)是隐层的输出向量,因此在ELM中,ncc为隐层节点数.为了简化表达,下文出现的x表示x(i),∀i=1,2,…,m,y(1),…,y(m)为输入向量对应的真实类别标签,其中,y(i)∈{1,2,…,ns},i=1,2,…,m.ns为类别个数,在ELM中,ns表示输出节点数.

定义一个概率函数π():ℝ1×ncc→[0,1]ns,该函数将输入向量x映射为一个ns维向量,其中,第u维π(x)u代表输入向量属于第u类的概率大小.基于以上定义,下面证明π()具有softmax函数形式.

根据π()的定义,可知π()应满足以下性质:

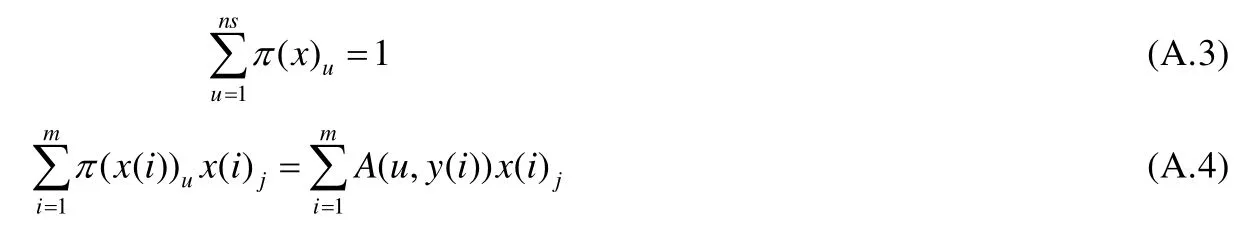
根据信息论,π()的熵可以定义为

根据信息论最大熵原理,即通常选取熵值最大的概率分布作为随机变量的分布,所以在公式(A.2)～公式(A.4)的约束下,最大化公式(A.5),该过程是一个求条件极值的问题,通常使用拉格朗日乘数法求解该问题.这里,拉格朗日方程可以写成:

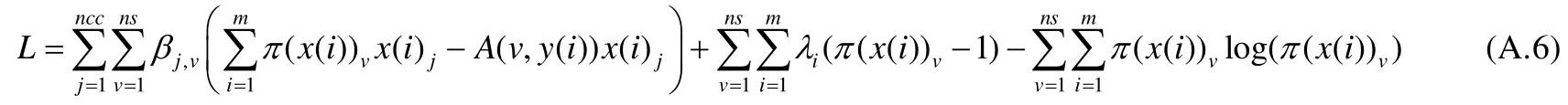
其中,βj,v与λi为拉格朗日乘数,且βj,v为矩阵β∈ℝncc×ns中的元素.注意到条件(A.2)为不等式,所以无法被包含进方程(A.6),但是可以在方程(A.6)的解中,选择满足条件(A.2)的值为最终解.在求解过程中,L对π(x(i))v求偏导,且极值在偏导数等于0处取得,即

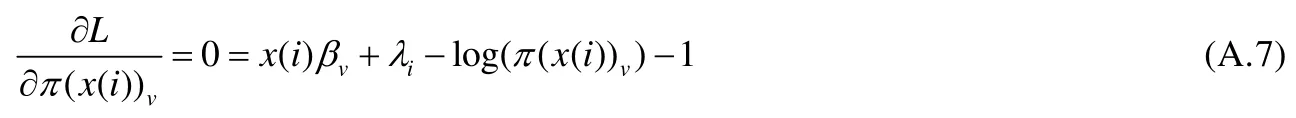
其中,βv∈ℝncc×1为β中第v列列向量.对公式(A.7)等价变形有:

根据公式(A.3),有:

即

公式(A.11)右侧分式上下同乘e,有:

公式(A.12)可以简化成:

在 ELM 中,βv可被看作是连接隐层与输出层第v个节点的权重向量,β是输出层权重,则x(i)βv是网络输出yiv;同理,x(i)βu=yiu.综上,证明满足概率性质的概率函数π()具有softmax的函数形式,从而证明用softmax函数作用在ELM的输出层输出后验概率的合理性. □

实验1的参数设置.

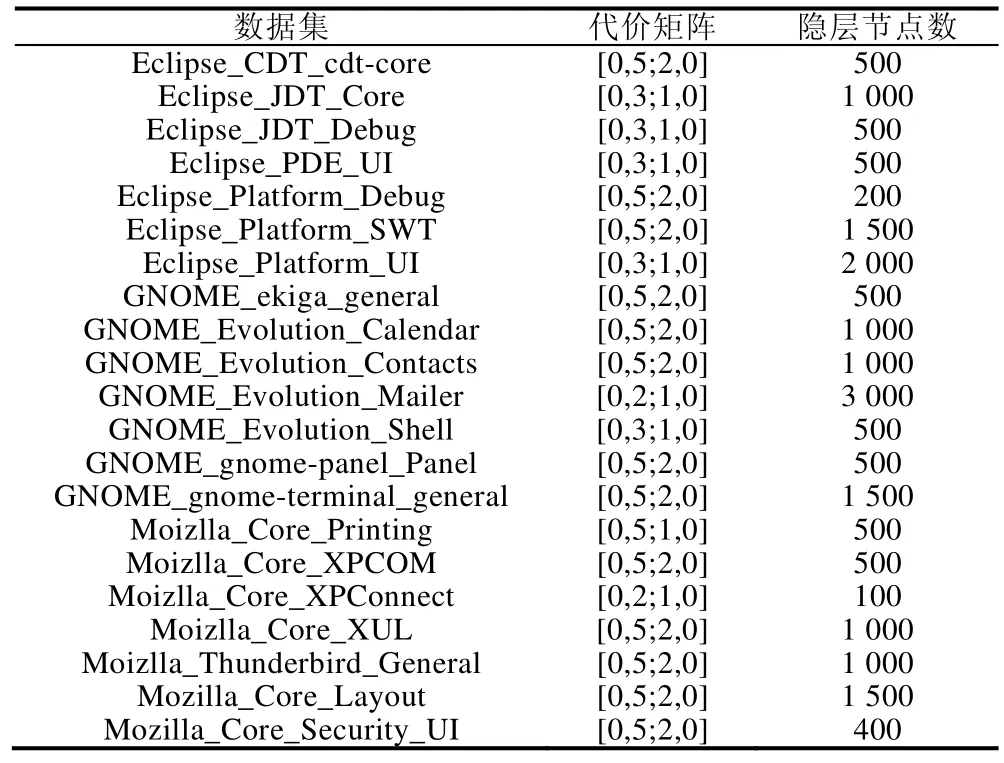
数据集 代价矩阵 隐层节点数Eclipse_CDT_cdt-core [0,5;2,0] 500 Eclipse_JDT_Core [0,3;1,0] 1 000 Eclipse_JDT_Debug [0,3,1,0] 500 Eclipse_PDE_UI [0,3;1,0] 500 Eclipse_Platform_Debug [0,5;2,0] 200 Eclipse_Platform_SWT [0,5;2,0] 1 500 Eclipse_Platform_UI [0,3;1,0] 2 000 GNOME_ekiga_general [0,5,2,0] 500 GNOME_Evolution_Calendar [0,5;2,0] 1 000 GNOME_Evolution_Contacts [0,5;2,0] 1 000 GNOME_Evolution_Mailer [0,2;1,0] 3 000 GNOME_Evolution_Shell [0,3;1,0] 500 GNOME_gnome-panel_Panel [0,5;2,0] 500 GNOME_gnome-terminal_general [0,5;2,0] 1 500 Moizlla_Core_Printing [0,5;1,0] 500 Moizlla_Core_XPCOM [0,5;2,0] 500 Moizlla_Core_XPConnect [0,2;1,0] 100 Moizlla_Core_XUL [0,5;2,0] 1 000 Moizlla_Thunderbird_General [0,5;2,0] 1 000 Mozilla_Core_Layout [0,5;2,0] 1 500 Mozilla_Core_Security_UI [0,5;2,0] 400

实验2的参数设置.

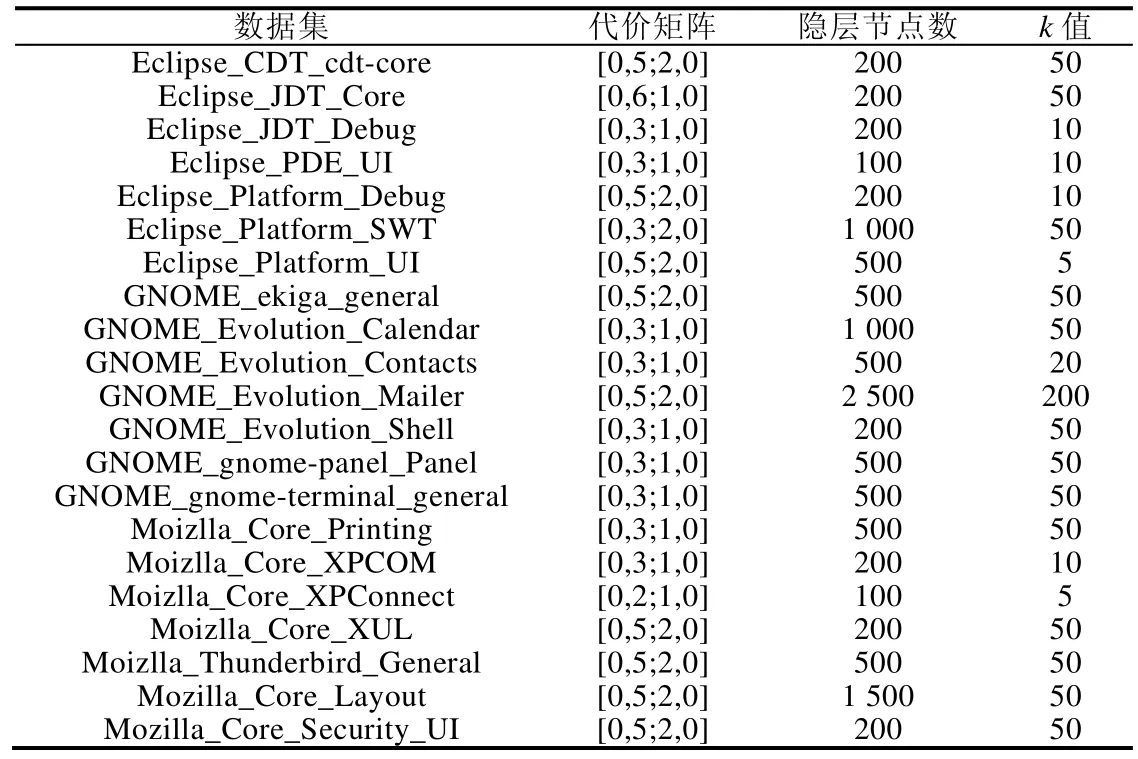
数据集 代价矩阵 隐层节点数 k值Eclipse_CDT_cdt-core [0,5;2,0] 200 50 Eclipse_JDT_Core [0,6;1,0] 200 50 Eclipse_JDT_Debug [0,3;1,0] 200 10 Eclipse_PDE_UI [0,3;1,0] 100 10 Eclipse_Platform_Debug [0,5;2,0] 200 10 Eclipse_Platform_SWT [0,3;2,0] 1 000 50 Eclipse_Platform_UI [0,5;2,0] 500 5 GNOME_ekiga_general [0,5;2,0] 500 50 GNOME_Evolution_Calendar [0,3;1,0] 1 000 50 GNOME_Evolution_Contacts [0,3;1,0] 500 20 GNOME_Evolution_Mailer [0,5;2,0] 2 500 200 GNOME_Evolution_Shell [0,3;1,0] 200 50 GNOME_gnome-panel_Panel [0,3;1,0] 500 50 GNOME_gnome-terminal_general [0,3;1,0] 500 50 Moizlla_Core_Printing [0,3;1,0] 500 50 Moizlla_Core_XPCOM [0,3;1,0] 200 10 Moizlla_Core_XPConnect [0,2;1,0] 100 5 Moizlla_Core_XUL [0,5;2,0] 200 50 Moizlla_Thunderbird_General [0,5;2,0] 500 50 Mozilla_Core_Layout [0,5;2,0] 1 500 50 Mozilla_Core_Security_UI [0,5;2,0] 200 50

实验3的参数设置.

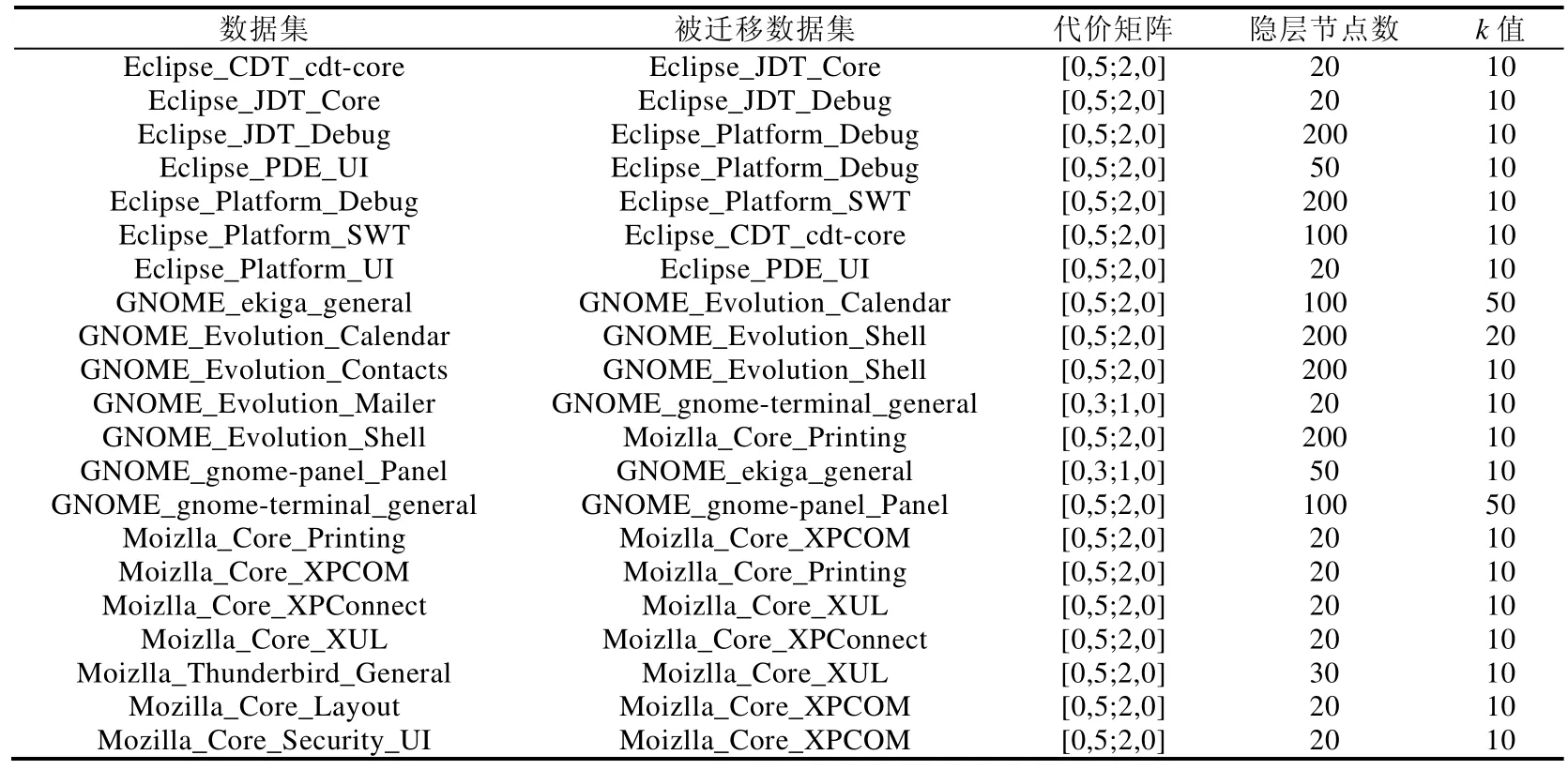
数据集 被迁移数据集 代价矩阵 隐层节点数 k值Eclipse_CDT_cdt-core Eclipse_JDT_Core [0,5;2,0] 20 10 Eclipse_JDT_Core Eclipse_JDT_Debug [0,5;2,0] 20 10 Eclipse_JDT_Debug Eclipse_Platform_Debug [0,5;2,0] 200 10 Eclipse_PDE_UI Eclipse_Platform_Debug [0,5;2,0] 50 10 Eclipse_Platform_Debug Eclipse_Platform_SWT [0,5;2,0] 200 10 Eclipse_Platform_SWT Eclipse_CDT_cdt-core [0,5;2,0] 100 10 Eclipse_Platform_UI Eclipse_PDE_UI [0,5;2,0] 20 10 GNOME_ekiga_general GNOME_Evolution_Calendar [0,5;2,0] 100 50 GNOME_Evolution_Calendar GNOME_Evolution_Shell [0,5;2,0] 200 20 GNOME_Evolution_Contacts GNOME_Evolution_Shell [0,5;2,0] 200 10 GNOME_Evolution_Mailer GNOME_gnome-terminal_general [0,3;1,0] 20 10 GNOME_Evolution_Shell Moizlla_Core_Printing [0,5;2,0] 200 10 GNOME_gnome-panel_Panel GNOME_ekiga_general [0,3;1,0] 50 10 GNOME_gnome-terminal_general GNOME_gnome-panel_Panel [0,5;2,0] 100 50 Moizlla_Core_Printing Moizlla_Core_XPCOM [0,5;2,0] 20 10 Moizlla_Core_XPCOM Moizlla_Core_Printing [0,5;2,0] 20 10 Moizlla_Core_XPConnect Moizlla_Core_XUL [0,5;2,0] 20 10 Moizlla_Core_XUL Moizlla_Core_XPConnect [0,5;2,0] 20 10 Moizlla_Thunderbird_General Moizlla_Core_XUL [0,5;2,0] 30 10 Mozilla_Core_Layout Moizlla_Core_XPCOM [0,5;2,0] 20 10 Mozilla_Core_Security_UI Moizlla_Core_XPCOM [0,5;2,0] 20 10

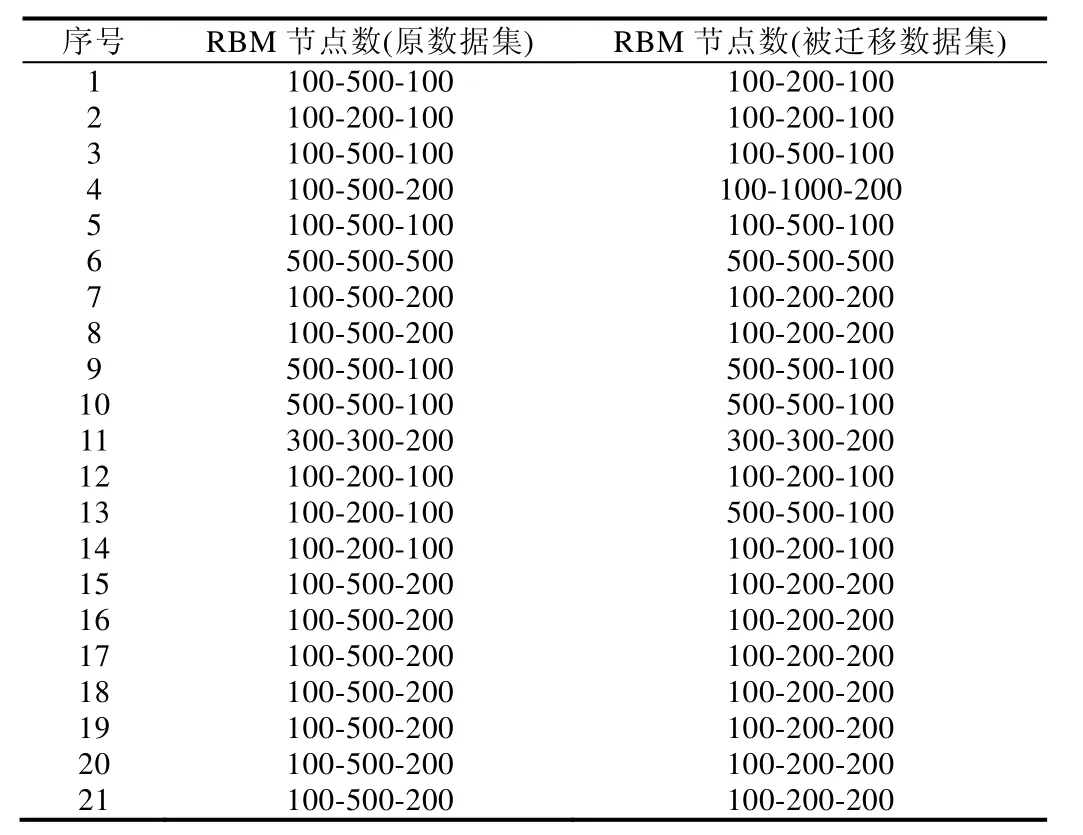
序号 RBM节点数(原数据集)RBM节点数(被迁移数据集)1 100-500-100 100-200-100 2 100-200-100 100-200-100 3 100-500-100 100-500-100 4 100-500-200 100-1000-200 5 100-500-100 100-500-100 6 500-500-500 500-500-500 7 100-500-200 100-200-200 8 100-500-200 100-200-200 9 500-500-100 500-500-100 10 500-500-100 500-500-100 11 300-300-200 300-300-200 12 100-200-100 100-200-100 13 100-200-100 500-500-100 14 100-200-100 100-200-100 15 100-500-200 100-200-200 16 100-500-200 100-200-200 17 100-500-200 100-200-200 18 100-500-200 100-200-200 19 100-500-200 100-200-200 20 100-500-200 100-200-200 21 100-500-200 100-200-200

实验4的参数设置.

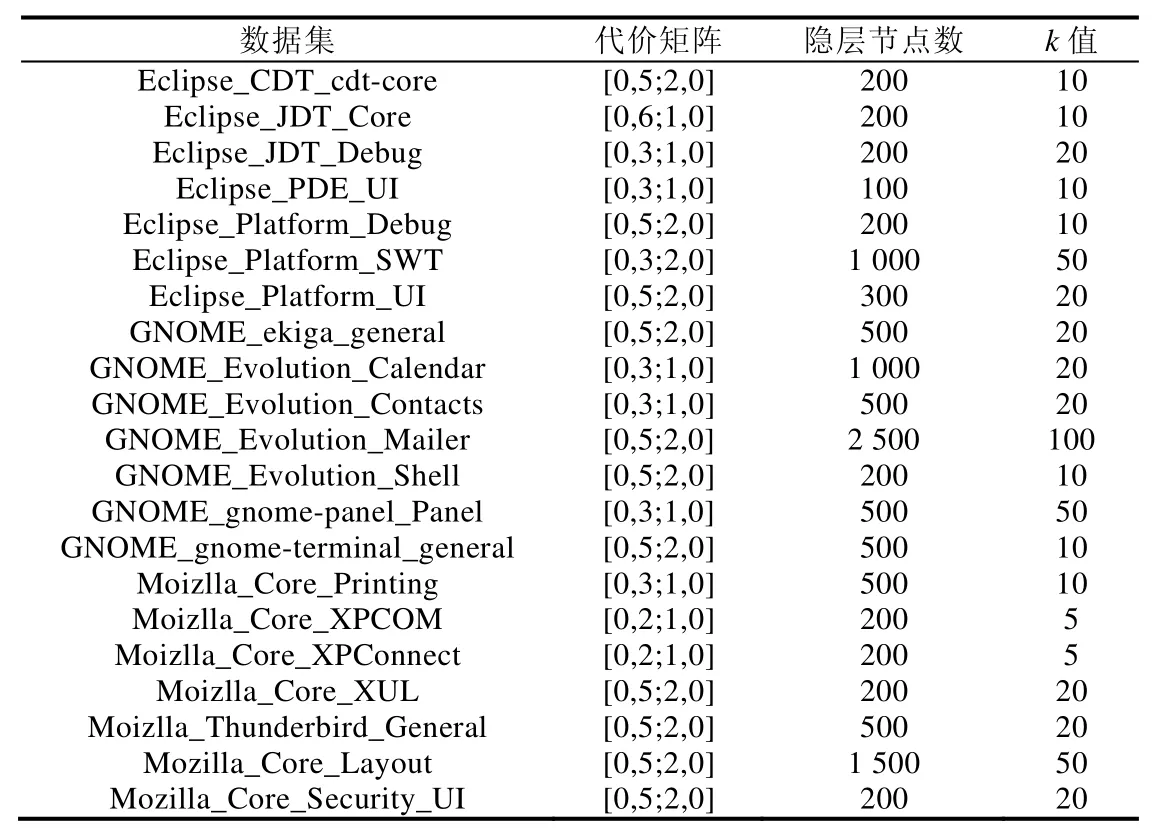
数据集 代价矩阵 隐层节点数 k值Eclipse_CDT_cdt-core [0,5;2,0] 200 10 Eclipse_JDT_Core [0,6;1,0] 200 10 Eclipse_JDT_Debug [0,3;1,0] 200 20 Eclipse_PDE_UI [0,3;1,0] 100 10 Eclipse_Platform_Debug [0,5;2,0] 200 10 Eclipse_Platform_SWT [0,3;2,0] 1 000 50 Eclipse_Platform_UI [0,5;2,0] 300 20 GNOME_ekiga_general [0,5;2,0] 500 20 GNOME_Evolution_Calendar [0,3;1,0] 1 000 20 GNOME_Evolution_Contacts [0,3;1,0] 500 20 GNOME_Evolution_Mailer [0,5;2,0] 2 500 100 GNOME_Evolution_Shell [0,5;2,0] 200 10 GNOME_gnome-panel_Panel [0,3;1,0] 500 50 GNOME_gnome-terminal_general [0,5;2,0] 500 10 Moizlla_Core_Printing [0,3;1,0] 500 10 Moizlla_Core_XPCOM [0,2;1,0] 200 5 Moizlla_Core_XPConnect [0,2;1,0] 200 5 Moizlla_Core_XUL [0,5;2,0] 200 20 Moizlla_Thunderbird_General [0,5;2,0] 500 20 Mozilla_Core_Layout [0,5;2,0] 1 500 50 Mozilla_Core_Security_UI [0,5;2,0] 200 20