基于频繁模式挖掘的GCC编译时能耗演化优化算法∗

倪友聪,吴 瑞,杜 欣,叶 鹏,李汪彪,肖如良

1(福建师范大学 数学与信息学院,福建 福州 350117)

2(武汉纺织大学 数学与计算机学院,湖北 武汉 430200)

3(福建师范大学 光电与信息工程学院,福建 福州 350117)

4(福建省公共服务大数据挖掘与应用工程技术研究中心(福建师范大学),福建 福州 350117)

能耗是嵌入式软件的关键质量属性,特别是在电量受限的执行环境中,降低嵌入式软件的能耗具有更为重要的价值和意义[1].与嵌入式软件源代码级的能耗优化相比,编译时能耗优化具有无需改动源代码,并且可保证功能语义一致性的优点.作为一款开源编译器,GCC[2]已广泛应用于嵌入式软件源代码的编译.GCC提供常用的几种优化等级,利用每种优化等级所预设的一组编译选项对软件源代码进行编译,能实现可执行代码的质量优化.然而,对于特定的软件源代码、特定的执行平台和特定的优化目标,GCC的优化等级往往难以获得最佳的优化效果.此外,GCC编译选项数目众多,选择空间十分庞大.例如GCC4.9.2提供了188个编译选项,其选择空间高达2188.依靠程序员人工选择编译选项不仅十分困难,而且也难以保证优化质量.更为重要的是,GCC提供的优化等级多集中于执行时间和目标代码大小的优化,而未针对能耗优化的场景.Pallister的研究成果[3]已表明,使用GCC的某些优化等级对嵌入式软件进行编译时,甚至出现能耗增加的情况.近年来,用于能耗优化的 GCC编译选项的选择问题已经成为了一个研究热点[4].基于Hoste等人[5]提出的58个常用于能耗优化的编译选项,已涌现出基于统计的方法、机器学习方法和演化算法这3类主要的优化方法[6].

基于统计的方法[7]运用 Mann-Whitney测试为特定的领域嵌入式软件确定一组有改进效果的编译选项.具体地,首先,将一组预设的编译选项应用于多个同类型嵌入式软件,考察在这组选项中去掉某一编译选项后的能耗变化情况;再根据Mann-Whitney测试的结果判断去掉该编译选项前后是否存在显著的差异,从而确定该编译选项是否对能耗有显著影响;最后,经过多组统计实验,可找出一组对某一类型嵌入式软件有能耗改进效果的编译选项.由于GCC编译选项众多且它们之间还存在复杂的影响关系,而基于统计的方法一次仅考查1个选项的模式难以最终获取对能耗改进效果最佳的编译选项集合.

机器学习方法[8-10]先通过对训练样本集使用机器学习算法训练得到模型,再利用模型预测与训练样本集同属一类的嵌入式软件的最优编译选项集合.训练样本集中的每个样本以某一嵌入式软件作为输入,并使用迭代编译的方法找到的最优编译选项集合作为输出.同类型的多个嵌入式软件及它们的最优编译选项集合组成了机器学习方法的训练样本集.然而,一些研究工作[10,11]已经实证了迭代编译方法不能在庞大的空间中找到最优编译选项集合.受制于训练样本自身的质量,使得机器学习方法得到的模型难以准确预测出真正的最优编译选项集合.

基于演化算法的方法[5,11-14]将编译时能耗优化问题抽象成一个编译选项选择优化问题,并针对特定的嵌入式软件和特定的执行平台搜索更大的编译选项选择空间,为进一步降低能耗提供了有力支持.Hoste等人运用传统遗传算法(genetic algorithm,简称 GA)[5,11]获取了比迭代编译和编译器预设的最高优化等级更好的编译选项集合.为了进一步提高解的质量和加快算法的收敛速度,Lin,Nagiub和 Garciarena又提出了一些新的演化算法.Lin等人[12]设计了一种基因加权的遗传算法,通过对上一代种群中适应度值高的个体所选择的编译选项加权,以影响变异概率,从而加快了收敛速度.Nagiub等人[13]通过设计新的 pass-over算子,将上一代种群中适应度优的个体直接加入到下一代种群,利用保留优势解的策略进一步加快了算法的收敛速度.但Lin等人和Nagiub等人的算法不仅存在过早收敛、易陷入局部最优的问题,而且也未考虑编译选项之间存在相互影响的情况.为了解决这些不足,Garciarena等人[14]提出了双变量相关分布评估算法(tree estimation of distribution algorithm,简称Tree-EDA).Tree-EDA算法考虑了任意两个编译选项之间可能存在的相互影响,并在多个案例下与 GA和单变量分布评估算法(univariate marginal distribution algorithm,简称 UMDA)[15]进行了对比实验,实验结果表明,Tree-EDA算法能获取比GA和UMDA更好的解质量和收敛速度.然而Tree-EDA仅考虑了任意两个编译选项之间的相互影响,而未涉及多个选项之间可能存在的相互作用.

为了探究多个编译选项之间的相互作用对解质量和收敛速度的影响,本文提出了一种基于频繁模式挖掘的遗传算法,并将其命名为GA-FP.GA-FP算法记录演化过程中有能耗改进效果的个体,并建立带能耗标注的事务表.GA-FP算法利用带能耗标注的事务表,并通过扩展传统的频繁模式树挖掘算法,挖掘出现频度高且能耗改进大的一组编译选项,并将其作为启发式信息,引入了“增添”和“删减”两种新的变异算子帮助提高解质量和加快收敛速度.通过与Tree-EDA在5个不同领域的8个典型案例下实验对比的结果表明,本文的GA-FP算法不仅能更有效降低软件能耗(平均降低2.5%,最高降低21.1%),而且还能在获得不劣于Tree-EDA能耗优化效果的前提下更快地收敛(平均加快34.5%,最高加快83.3%);最优解中编译选项的相关性分析,进一步验证了所设计变异算子的有效性.

本文第1节给出问题描述.第2节阐述GA-FP算法的总体流程.第3节详细介绍挖掘带能耗改进标注的频繁编译模式集.第 4节提出“增添”和“删减”两个变异算子.第 5节给出案例研究及实验结果.第 6节总结全文并给出未来工作.

1 问题描述

下面给出用于嵌入式软件能耗优化的GCC编译选项选择问题的形式化描述.

定义1(优化空间Ω).若对GCC编译器支持的编译选项从1至l进行编号,则优化空间Ω可定义为公式(1)所示的l元序偶集.

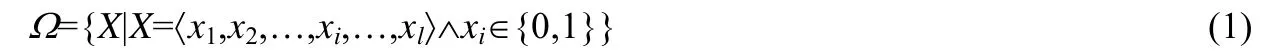
其中,xi=0或1分别表示选用或不选用编译选项i.

定义2(选用和未选用的编译选项集).对于优化空间Ω中一个元素X,其所定义的选用和未选用的编译选项集分别用SS(X)和SU(X)表示.它们分别由公式(2)和公式(3)定义.

定义3(能耗评估).能耗评估函数EvE(Sftexe)用于计算一个嵌入式软件可执行代码Sftexe在某一特定输入下,从开始运行至结束所消耗的电能(如图1所示).

Fig.1 Schematic diagram of energy consumption calculation图1 能耗计算示意图

EvE(Sftexe)的定义如公式(4)所示.

其中,Tj和Tj+1分别表示Sftexe在特定输入下,执行过程中的第j和j+1功率测量的采样点;T0和Tn分别为Sftexe执行的开始时刻和结束时刻;Pj和Pj+1分别表示第j和j+1采样点测得的瞬时功率.通过累加相邻两个采样时刻点和对应功率所形成的梯形的面积,可计算Sftexe执行过程中实际能耗的近似值.基于STM32F4开发板,我们研发了一套能耗评估系统,实现了EvE(Sftexe)函数的功能.

定义4(编译和链接).定义函数cmpLnk0(Sftsrc)和函数cmpLnk(Sftsrc,X)分别表示运用GCC编译器缺省的-O0等级(不选用任何编译选项)、SS(X)选用的编译选项集,对一个嵌入式软件源代码Sftsrc进行编译和链接后所得到的可执行代码.

定义5(目标函数).定义函数f(Sftsrc,X)用于计算相对于-O0等级,使用SS(X)编译选项集获得Sftsrc对应的可执行代码在运行时能耗所降低的百分比.f(Sftsrc,X)的定义如公式(5)所示.

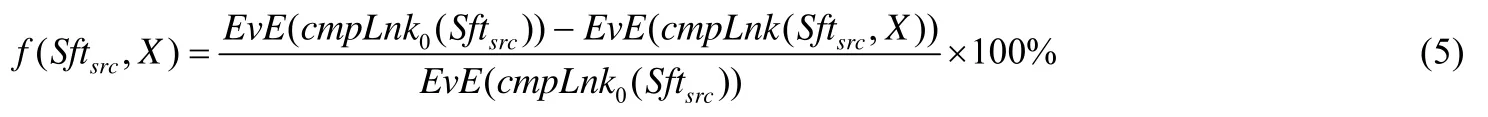
定义6(优化问题).用于嵌入式软件能耗优化的编译选项选择问题可描述为搜索满足公式(6)的最优解X*.

2 GA-FP算法流程

GA-FP算法用于求解公式(6)定义的优化问题,它在传统遗传算法[16]中融入了频繁模式挖掘和启发式变异的方法,其流程见表1.

Table 1 Flow of GA-FP algorithm表1 GA-FP算法的流程

GA-FP算法主要包括初始化随机种群、计算种群中个体的适应度值、更新带能耗改进标注的编译选项事务表、挖掘带能耗改进标注的频繁编译选项模式集、种群中个体做交叉操作、种群中个体做启发式变异操作、按轮盘赌选择出下一代种群等主要步骤.下面仅对与频繁模式挖掘和启发式变异相关的步骤作简要介绍.

· 更新带能耗改进标注的编译选项事务表发生在每个个体的适应度值计算后.具体地,通过表1中的第7步～第 13步,将有能耗改进效果的个体Xk的信息作为一条事务收集到形如表2的事务表TTE(the transaction table with energe annotations of compilation options)中.每条事务TE(a transaction with energe annotations)是三元组(编译选项编号、出现次数和能耗改进标注)的有序列表,它用于依次保存Xk选用的一组编译选项及能耗改进效果的信息.为了便于挖掘,在TE的每个三元组中,出现次数固定为 1、能耗改进标注值为Xk相对于GCC的-O0等级降低能耗的百分比(对应于f(Sftsrc,Xk)).能耗改进标注表达了一个编译选项参与了多大能耗改进幅度的事务.

· 挖掘带能耗改进标注的频繁编译选项模式集(表1中的第15步)以及“增添”和“删减”两种启发式变异操作(表1中的第19步～第23步)将分别在下面的第3节和第4节给予详细的阐述.

Table 2 An example for transaction tableTTEwith energy consumption annotations of compilation options表2 带能耗改进标注的编译选项事务表TTE的例子

3 挖掘带能耗改进标注的频繁编译选项模式集

与一般的事务不同,表2中每个事务TE中的每个编译选项被标注了所参与事务的能耗改进信息,因而在挖掘过程中不仅需要考虑各个编译选项在事务表中出现的频度,而且还要体现各个编译选项所参与事务的能耗改进情况.文中通过扩展经典的频繁模式树挖掘算法[17],挖掘出带能耗改进标注的频繁编译选项模式集.下面先给出与频繁编译选项模式相关的定义,然后介绍与带能耗改进标注的频繁模式树(简记为FPE树)的数据结构,再阐述基于FPE树的挖掘算法,最后给出一个例子来解释整个频繁编译选项模式集的挖掘过程.

3.1 与频繁编译选项模式相关的定义

定义7(编译选项的支持计数).i号编译选项的支持计数cnt(i)由公式(7)和公式(8)定义.

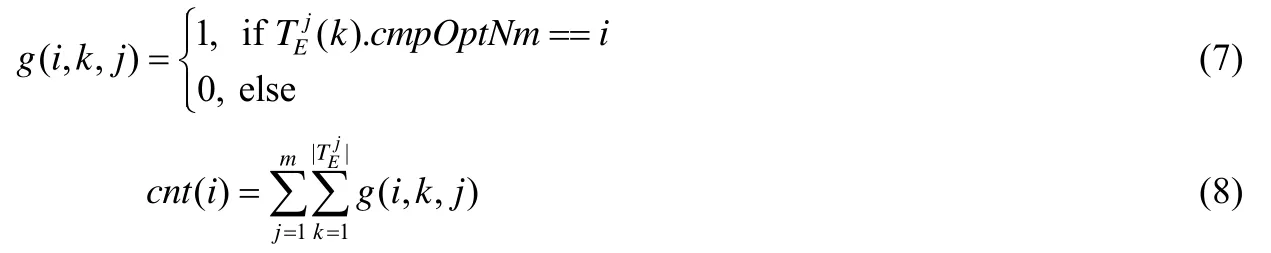
从定义7和定义8不难看出,cnt(i)是i号编译选项在整个事务表TTE中出现的次数.例如在表2的例子事务表TTE中,cnt(1)=3.

定义8(频繁编译选项).称i号编译选项是一个频繁编译选项,当且仅当cnt(i)大于或等于预设的最小支持计数Cmin.

定义9(编译选项集的支持计数).若ScmpOptNm是编译选项编号的集合,则ScmpOptNm对应的编译选项集的支持计数用cntS(ScmpOptNm)进行表示.cntS(ScmpOptNm)由公式(9)和公式(10)定义.

从公式(9)和公式(10)不难看出,cntS(ScmpOptNm)是ScmpOptNm的各个编译选项在事务表TTE各条事务中同时出现的次数.例如在表2的例子事务表TTE中,6号和3号组成的编译选项集{6,3}的支持计数cntS({6,3})=3.

定义 10(频繁编译选项模式).若ScmpOptNm和Cmin分别是编译选项编号的集合和预设的最小支持计数,则ScmpOptNm对应的编译选项集是频繁编译选项模式,当且仅当cntS(ScmpOptNm)≥Cmin.

定义11(带能耗改进标注的频繁编译选项模式).设fpcmpOpt是带能耗改进标注的编译选项集合:

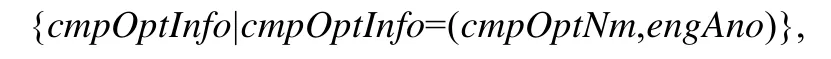
其中,cmpOptNm和engAno分别表示编译选项编号和能耗改进标注.若投影fpcmpOpt中每个元素的cmpOptNm而获得的编译选项集是满足定义10的频繁编译选项模式,则称fpcmpOpt是一个带能耗改进标注的频繁编译选项模式.当|fpcmpOpt|=k,称fpcmpOpt为带能耗标注的k频繁编译选项模式,并简记为.

3.2 FPE树的数据结构

与传统FP树[17]的数据结构类似,FPE树也是由前缀项树PT和项头表HL所构成,但FPE树融入了能耗标注,如图2所示.前缀项树 PT包含一个根结点root和若干棵前缀项子树,PT树的每个结点用cmpOptNm,count,engAno,parNode和nextNode这5个属性描述,它们分别表示编译选项编号、编译选项出现次数、能耗改进标注、指向父结点的指针和指向下一个具有相同编译选项编号的结点的指针.在图2椭圆形表示的结点中,逗号分隔的3个数值分别是cmpOptNm,count和engAno的值,而根结点root中的这3个数值为空null.图2中,实线和虚线弧间接定义了每个结点的parNode和nextNode的值.没有虚线弧的结点,其nextNode值为空null.与传统FP树不同之处在于,FPE树的结点引入了能耗改进标注的描述.

Fig.2 FPE tree derived from the example transaction tableTTEshown in table 2图2 基于表2例子事务表TTE生成的FPE树

项头表HL的每个表项用cmpOptNm和hdLnk两个属性进行描述,这两个属性分别表示编译选项编号和结点链(虚线弧构成的链)的头指针.通过结点链,可将同一个编译选项链接起来.例如,图2中项头表HL最后一行的头指针hdLnk将前缀树PT中所有出现16号编译选项的结点(灰色背景指示)链接起来.

3.3 基于FPE树的挖掘算法

表3给出了带能耗改进标注的频繁编译选项模式的挖掘算法FPE-growth.当以带能耗改进标注的编译选项事务表TTE和最小支持计数Cmin作为参数调用 FPE-growth,可输出频繁编译选项模式集表,其包含了所有的k频繁编译选项模式集.对图2的FPE树运用FPE-growth算法可输出表4所示的频繁编译选项模式集表.

Table 3 FPE-growth algorithm表3 FPE-growth算法

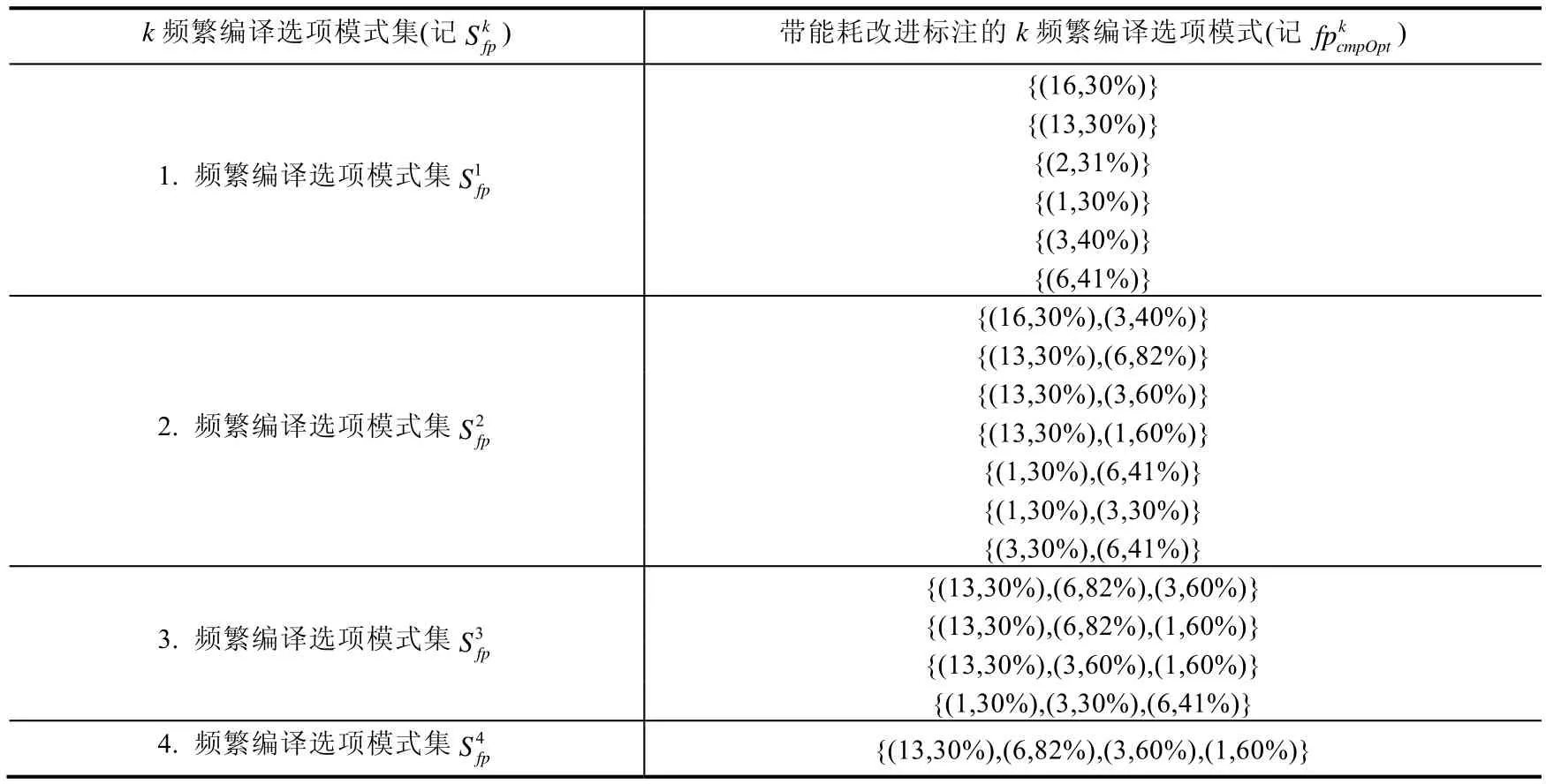
Table 4 Table for the set of frequent pattern of compilation options with energy annotations in the example表4 例子的带能耗改进标注的频繁编译选项模式集表

3.4 算法执行的实例

本节将FPE-growth算法的一个输入参数事务表TTE设为表2所示的事务表,另一个输入参数最小支持计数Cmin设为3,阐述FPE-growth算法执行过程.下面通过该算法中构建初始FPE树、在FPE树中插入频繁编译选项和挖掘带能耗改进标注的频繁编译选项模式集表等关键步骤进行说明.

· 步骤1.基于表2所示的带能耗改进效果的事务表TTE,生成一棵如图3所示的初始FPE树,包括前缀项树PT和项头表HL.

· 步骤2.通过扫描事务表TTE按最小支持计数3筛选出频繁编译选项,并按照支持计数降序排列,生成一张如表5所示排序后的频繁编译选项事务表TTFE.

· 步骤3.将频繁编译选项事务表TTFE各事务中的频繁编译选项按行依次插入到FPE树,最终获得如图2所示的FPE树.具体细节如下.

➢ 插入表5事务表TTFE第1行事务中的各频繁编译选项.由于每次递归插入时,根结点root没有匹配的孩子结点,故依次生成5个新结点,建立FPE树的第1个分支,如图4所示.

➢ 插入表4事务表TTFE第2行事务中各频繁编译选项.在图4的FPE树基础上,将表5事务表TTFE第2行事务的各频繁编译选项依次插入到FPE树时,由于插入第1个频繁编译选项(其编号、支持计数和能耗改进标注分别为6、1和10%)时,root结点有一个匹配的孩子结点(如图4灰色背景的结点,其支持计数和能耗改进标注分别为 1和 12%),需要将这个孩子结点的计数和能耗改进标注分别与表5第2行事务中6号编译选项的支持计数和能耗改进标注进行累加并更新为count=2和engAno=22%.类似地,插入表5第2行的第2和第 3个频繁编译选项.而当插入第 4个频繁编译选项(其编号、支持计数和能耗改进标注分别为 2、1和 10%)时,此时的根结点(1,2,22%)下没有匹配的孩子结点,在根结点(1,2,22%)下新建一个孩子结点,并将表3第2行事务中2号编译选项的支持计数和能耗改进标注赋值给该孩子结点的对应属性,从而得到 FPE树的第2个分支.同理,将第5个频繁编译选项插入到FPE树得到图5所示的FPE树.

➢ 依次插入表5第3行～第5行事务中的各编译选项,可输出表2事务表TTE对应的FPE树,如图2所示.

· 步骤4.基于步骤3得到的FPE树,使用挖掘算法获取如表4所示的带能耗改进标注的频繁编译选项模式集.

Fig.3 Initial FPE tree in the example图3 例子初始的FPE树

Table 5 Transaction tableTTFEof frequent compilation options obtained by selecting and sorting the transaction tableTTE表5 对事务表TTE进行筛选和排序后获取的频繁编译选项事务表TTFE

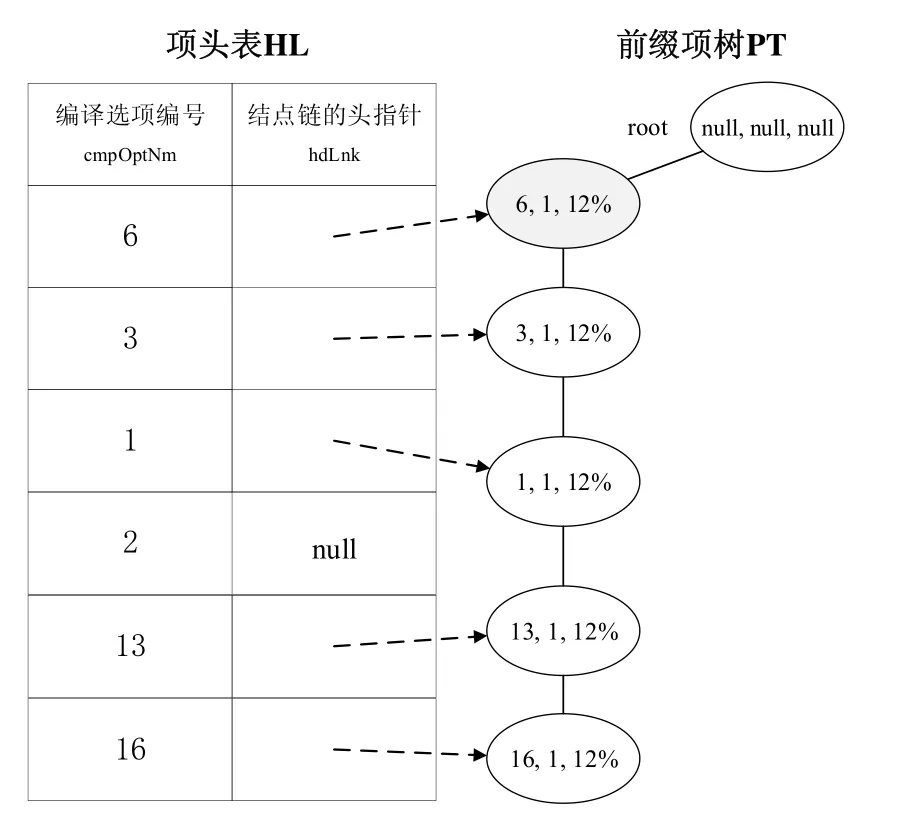
Fig.4 FPE tree obtained by inserting frequent compilation options of 1st row in Table 5 TTFE图4 将表5事务表TTFE第1行事务中各频繁编译选项插入后得到的FPE树

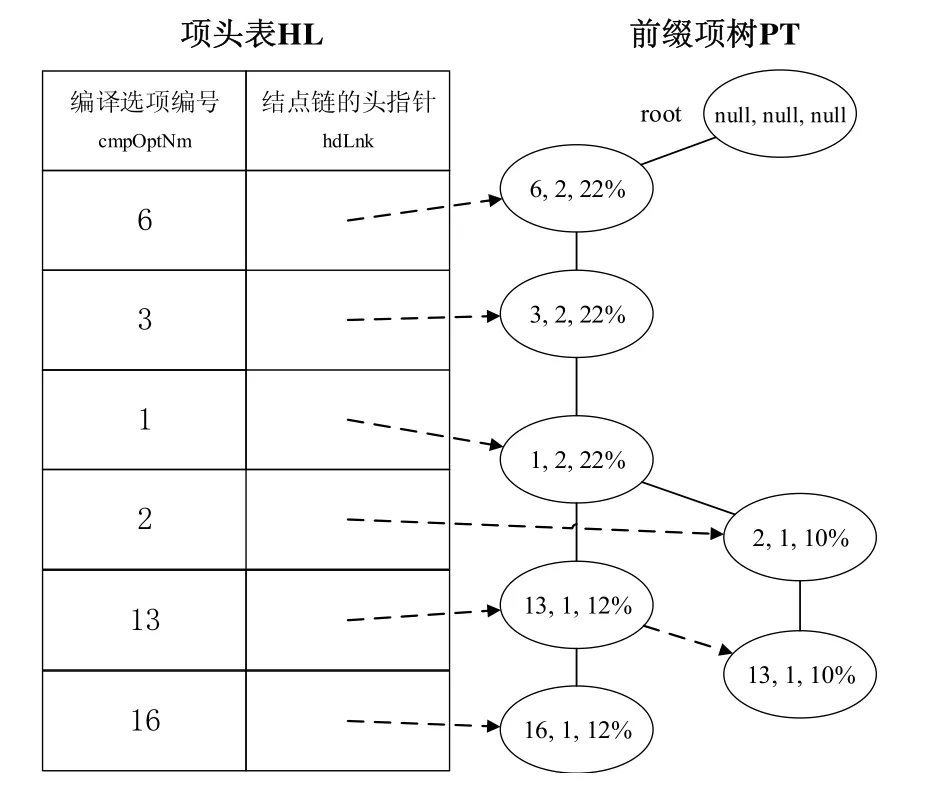
Fig.5 FPE tree obtained by inserting frequent compilation options of 1st and 2nd rows in Table 5TTFE图5 将表5事务表TTFE第1行和第2行事务中各频繁编译选项插入后得到的FPE树

4 变异操作

GA-FP算法引入了“增添”和“删减”作为两种启发式变异操作,这两种操作以带能耗改进标注的频繁编译选项模式集为启发式信息,下面给出相关定义后,再给出它们的具体操作步骤.

4.1 变异操作相关定义

定义12(频繁编译选项模式的加1匹配).若SS(X)和SU(X)分别是个体X指示的已选用和未选用的编译选项编号集,并且从SS(X)中随机选取k个元素(1≤k≤|SS(X)|)构成编译选项编号集合为ScmpOptNm,则ScmpOptNm的频繁编译选项模式的加1匹配由公式(11)定义.

例如,个体X={0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1},则SS(X)={3,5,9,10,11,13,14,16},SU(X)={1,2,4,6,7,8,12,15}.挖掘获得的带能耗改进标注的频繁编译选项模式集如表4所示.设从SS(X)中随机选取2个元素构成的编译选项编号集合为ScmpOptNm={3,13},从表4的频繁编译选项模式集中对应的4行可分别投影出4个编译选项编号集:{13,6,3},{13,6,1},{13,3,1},{1,3,6}.仅第1个和第3个集合包含ScmpOptNm={3,13},并且这两个集合与ScmpOptNm的差集都被SU(X)包含,故fpMatch+({3,13})={{(13,30%),(6,82%),(3,60%)},{(13,30%),(3,60%),(1,60%)}}.

定义13(频繁编译选项的加1匹配).若ScmpOptNm是从个体X的已选用编译选项编号集中随机抽取大小为k的子集,ScmpOptNm的频繁编译选项模式加1匹配为fpMatch+(ScmpOptNm),并且fpMatch+(ScmpOptNm)不空,则ScmpOptNm的频繁编译选项加1匹配fCOptMatch+(ScmpOptNm)由公式(12)定义.

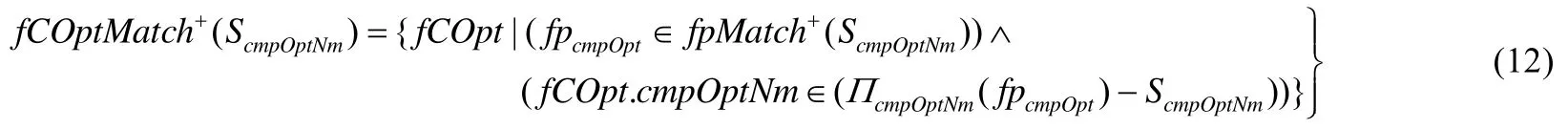
其中,fCOpt.cmpOptNm表示频繁编译选项fCOpt的编译选项编号.

例如,在上例的fpMatch+({3,13})中,两个频繁编译选项模式可分别投影出 2个编译选项编号集{13,6,3},{13,3,1}.这两个集合与ScmpOptNm={3,13}的差集分别为{6},{1}.根据差集,可从fpMatch+({3,13})中获取.

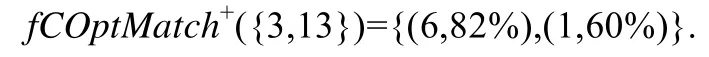
定义 14(频繁编译选项模式的减 1匹配).若个体X的已选用和未选用的编译选项编号集分别为SS(X)和SU(X),并且从SS(X)中随机选取k个元素(1≤k≤|SS(X)|)构成编译选项编号集为ScmpOptNm,则ScmpOptNm的频繁编译选项模式减1匹配fpMatch-(ScmpOptNm)由公式(13)定义.

例如,个体X={0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1},则SS(X)={3,5,9,10,11,13,14,16},SU(X)={1,2,4,6,7,8,12,15}.

挖掘获得的带能耗改进标注的频繁编译选项模式集如表4所示.设从SS(X)中随机选取2个元素构成的编译选项编号集合为ScmpOptNm={3,16},从表4的频繁编译选项模式集包含 6个元素:{(16,30%)},{(13,30%)},{(2,31%)},{(1,30%)},{(3,40%)}和{(6,41%)}.仅第1和第5个元素的编译选项编号被包含于ScmpOptNm={3,16},故

4.2 增添操作

表6给出了按增添操作的具体流程.当个体X没有选用任何编译选项,则采取随机单点变异方式将X的一位由0变1;否则,实施启发式增添编译选项.下面沿用定义12和定义13中使用的例子解释增添操作过程中的启发式变异.

设个体X={0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1},则SS(X)={3,5,9,10,11,13,14,16},SU(X)={1,2,4,6,7,8,12,15}.挖掘获得的带能耗改进标注的频繁编译选项模式集见表4.假定表6第5步从SS(X)中随机选取k=2个元素组成待变异的编译选项编号集合为ScmpOptNm={3,13},根据定义13可得fCOptMatch+({3,13})={(6,82%),(1,60%)},其过程分析见定义13的例子说明.故表6第6步得到频繁编译选项集SfCOpt={(6,82%),(1,60%)}.由表6第10步知:

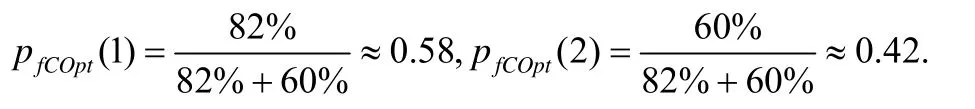
因而,分别以0.58和0.42概率选择6号和1号编译选项.假设选中6号编译选项,则通过表6第13步将X下标为6的码值替换成1,得到了新个体X′={0,0,1,0,1,1,0,0,1,1,1,0,1,1,0,1}.

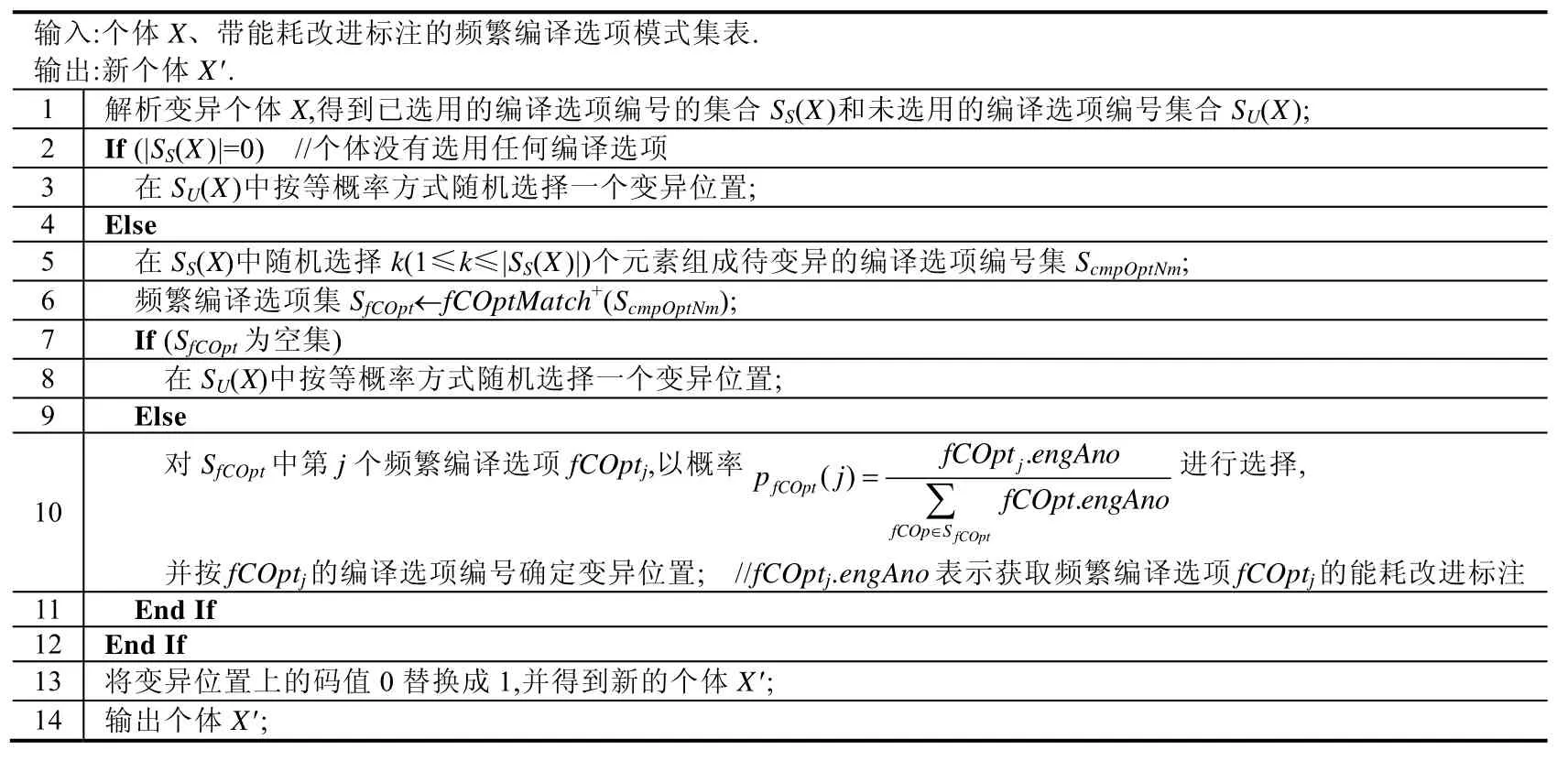
Table 6 Flow of “Add” operation表6 “增添”操作的流程

4.3 删减操作

表7给出了按删减操作的具体过程.

若个体X没有选用任何编译选项,则不做删减操作.当个体X仅选用 1个编译选项,则删减这个编译选项.除此两种情况外,实施启发式删减编译选项.沿用定义14所举的例子说明删减操作过程的启发式变异.

假定个体X={0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1},则SS(X)={3,5,9,10,11,13,14,16},SU(X)={1,2,4,6,7,8,12,15}.挖掘获得的带能耗改进标注的频繁编译选项模式集如表4所示.设表7第6步从SS(X)中随机选取k=2个元素构成的编译选项编号集合为ScmpOptNm={3,16},根据定义14可得fpMatch-({3,16})={{(16,30%)},{(3,40%)}},其过程分析见定义14下的例子说明.因而,表7第7步得到SfCOpt={{(16,30%)},{(3,40%)}}.由表7第11步可知,

故分别以0.57和0.43概率选择16号和3号编译选项.假设选中16号编译选项进行移除,而保留潜在能耗效果改进更好的3号编译选项.通过表7第15步,将X下标为16的码值替换成0,得到了新个体:

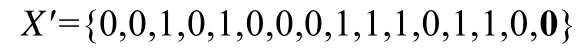
5 案例研究

本节给出了案例研究.第5.1节简介了实验案例.第5.2节提出了要验证的问题及度量标准.第5.3节说明了实验中使用的统计方法.第5.4节介绍了实验安装.第5.5节展示了实验结果并进行了分析.

5.1 案例简介

本文从BEEBS平台[18]中选用涵盖安全、网络、通信、汽车和消费这5个领域的8个案例,表8给出了这些案例的应用领域和代码量.

Table 8 Application domains and code size in the experimental cases表8 实验案例的应用领域和代码量

5.2 研究问题及其度量指标

问题1(解质量).本文GA-FP算法较之Tree-EDA算法能否得到更优的编译选项组合,使得案例的运行能耗更低?Tree-EDA是目前以能耗为优化目标并可获取较优编译选项组合的一种算法.通过回答这一问题,可以验证GA-FP算法的有效性.

度量指标.将 GA-FP和 Tree-EDA最优解对应的能耗相对改进百分比IΔeng%作为度量指标.在案例源代码Sftsrc下,IΔeng%的定义如公式(14)所示,其值越大越好.

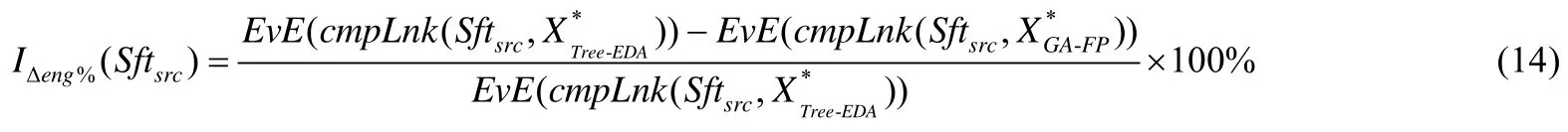
其中,

问题2(收敛速度).与Tree-EDA算法相比,GA-FP算法能否加快收敛速度?通过回答这一问题进一步验证GA-FP算法的有效性.

度量指标.为了公平比较两种算法的收敛速度,将 GA-FP达到不劣于 Tree-EDA最优解对应最小迭代次数的相对减少百分比IΔi%作为度量指标.在案例源代码Sftsrc下,IΔi%的定义如公式(15)所示,其值越大越好.

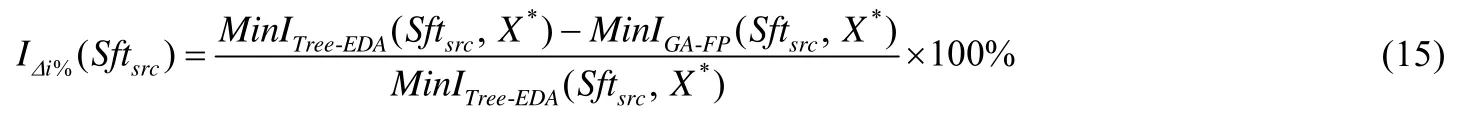
其中,MinTree-EDA(Sftsrc,X*)和MinGA-FP(Sftsrc,X*)分别表示在案例源代码Sftsrc下,Tree-EDA和GA-FP获取最优解X*所需要的最小迭代次数.

问题3(最优解中编译选项的正相关性).与Tree-EDA算法相比,本文GA-FP算法所获得的最优解中编译选项之间是否存在更强的正相关性?依赖于具体的软件源代码和执行平台中与能耗相关的特征,GCC多个编译选项之间呈现不相关、负相关和正相关等不同的影响关系.通过回答这一问题,可揭示 GA-FP比 Tree-EDA获得更好的解质量和更快的收敛速度的原因.亦即 GA-FP在出现频度高且对能耗有显著改进效果的一组编译选项基础上,引入的启发式变异应使得获取的最优解中包括更多正相关的编译选项.

度量指标.一组正相关编译选项是指:若从中移除任何一个选项,将使能耗的优化效果显著变差.考虑到GA-FP和Tree-EDA最优解中包含的编译选项在数目上的差异,将正相关选项在最优解中所占的比例作为度量指标IPC%(X*),以公正地比较最优解中各选项间的正相关性.IPC%(X*)的定义如公式(16)所示,其值越大越好.

其中,X+表示从最优解X*选用的编译选项开始.运用文献[7]提出的正交数组和曼-惠特尼秩和检验相结合的方法,得到的正相关的编译选项集.

问题4(编译选项的使用频度).在GA-FP算法对8个案例能耗优化结果中,各个编译选项的使用频度如何?通过对每个编译选项使用频度的分析,可以帮助人们在选用GCC编译选项时给出一些有用的借鉴和参考.

度量指标.在 GA-FP算法m次运行各个案例的结果中,每个编译选项xi的使用频度Ifq%(xi)作为度量指标,其定义如公式(17)所示.

其中,useNum(xi,k,j)表示GA-FP算法在第k次运行第j个案例所得最优解中编译选项xi的使用次数.Ifq%(xi)的值越大,说明编译选项xi在8个案例中的使用频度越高.

5.3 使用的统计方法

考虑到演化算法的随机性,GA-FP算法和Tree-EDA算法被分别独立运行20次,并进行统计检验.本文采用Wilcoxom秩和检验[19]方法对实验数据进行统计分析,并将置信水平α的值设置为 0.05.为了进一步观测对比数据的差异程度(effect size),本文还使用Vargha-Delaney[19]的作为effect size的直观度量.的值域为[0,1],其值越大,说明差异程度越大.

5.4 实验安装

(1) 实验环境

上位机的运行环境为Intel(R) Core(TM)i5-4590,3.30GHz处理器,8G内存及ubuntu-16.04.1操作系统.能耗评估系统是基于STM32F4板自主研发.被优化案例软件的运行环境采用STM32F103板.编译器和编译选项使用GCC4.9.2,并选用与Tree-EDA[14]相同的58个编译选项.

(2) 算法参数的设定

为了公平起见,GA-FP尽可能采用与Tree-EDA 相同的参数设定.表9给出了GA-FP和Tree-EDA的参数设定.表9中的符号NA表示GA-FP或Tree-EDA不包含对应的参数.

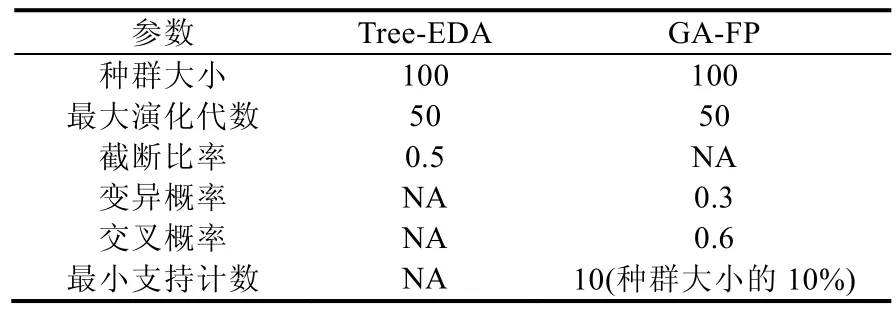
Table 9 Parameter settings of Tree-EDA and GA-FP表9 Tree-EDA和GA-FP的参数设定

5.5 实验结果及分析

下面具体给出问题1和问题2的实验结果及分析.

(1) 问题1(解质量)的实验结果及分析

表10给出了8个案例下-O0等级和-O3最优等级以及GA-FP和Tree-EDA算法20次运行最优解对应的能耗情况.从表10可以看出,对于每个案例,GA-FP和Tree-EDA在平均情况和最好情况下都能获取比-O3等级更优的编译选项集;GA-FP在最坏情况下对于全部案例也能得到优于-O3等级的编译选项集,而Tree-EDA在2D FIR和Float_Matrix两个案例却得到劣于-O3等级的结果;并且对于所有8个案例,GA-FP算法在平均情况、最坏情况和最好情况下都获得了比Tree_EDA和-O3等级更优的编译选项集.

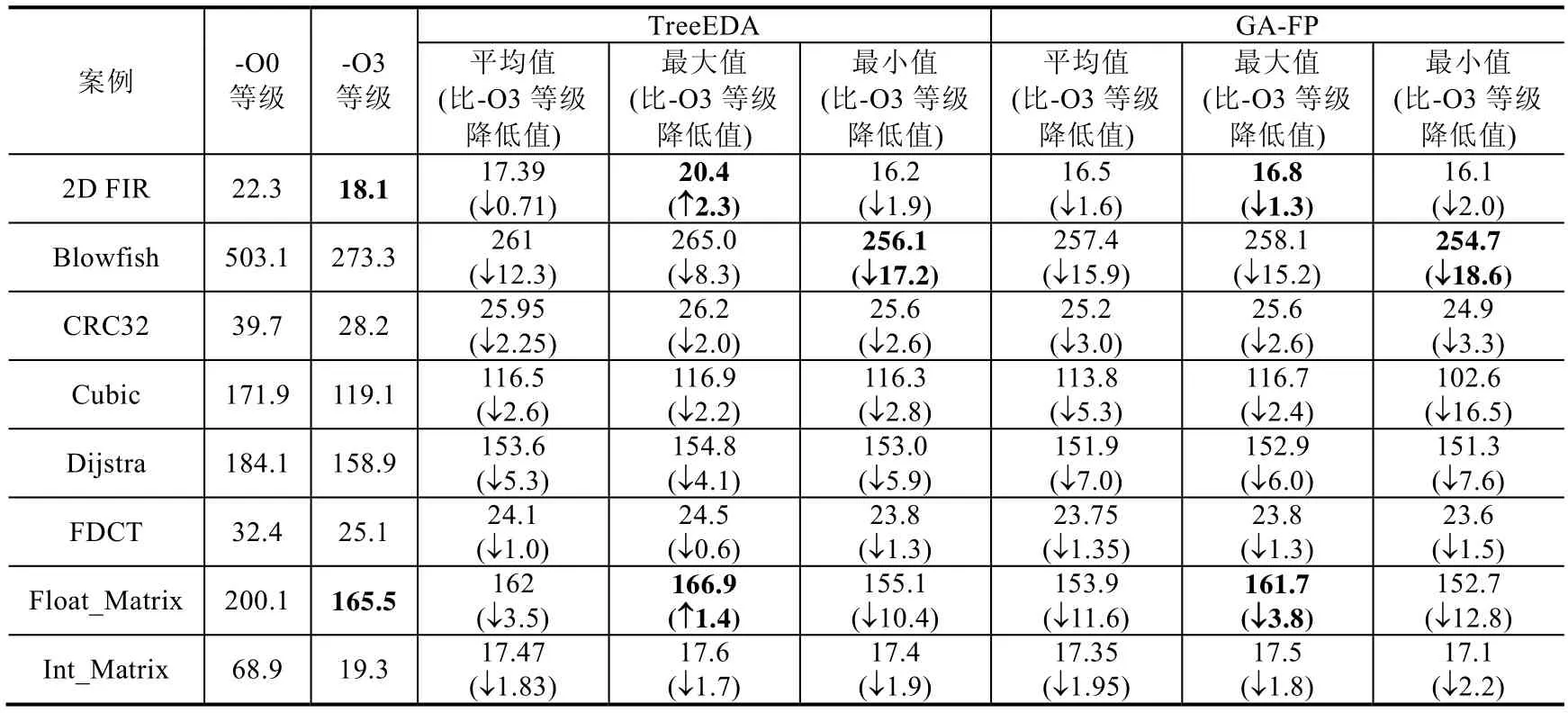
Table 10 Energy consumption of the optimal solutions obtained by -O0 level,-O3 level,Tree-EDA and GA-FP by 20 runs in 8 cases (J)表10 8个案例下-O0和-O3最优等级以及GA-FP和Tree-EDA算法20次运行最优解对应的能耗 (J)

表11进一步给出了GA-FP和Tree-EDA在8个案例下能耗改进百分比(IΔeng%)的秩和检验结果.

表11中第2列p-value值均小于置信水平0.05.这表明在8个案例下GA-FP的IΔeng%指标在统计意义上显著优于Tree-EDA.从表11中第3列的effect size值可以看出,GA-FP算法在Crc32和Dijstra两个案例下,以概率1优于Tree-EDA;在2D FIR、Blowfish、Cubic、FDCT、Float_Matrix和Int_Matrix这6个案例下,以较大概率在解质量上优于Tree-EDA.

图6所给出的统计盒图也从直观上得到一致结论.

从表12的统计量结果可知,8个案例下的IΔeng%指标平均值为2.5%,最大IΔeng%指标值可达21.1%.

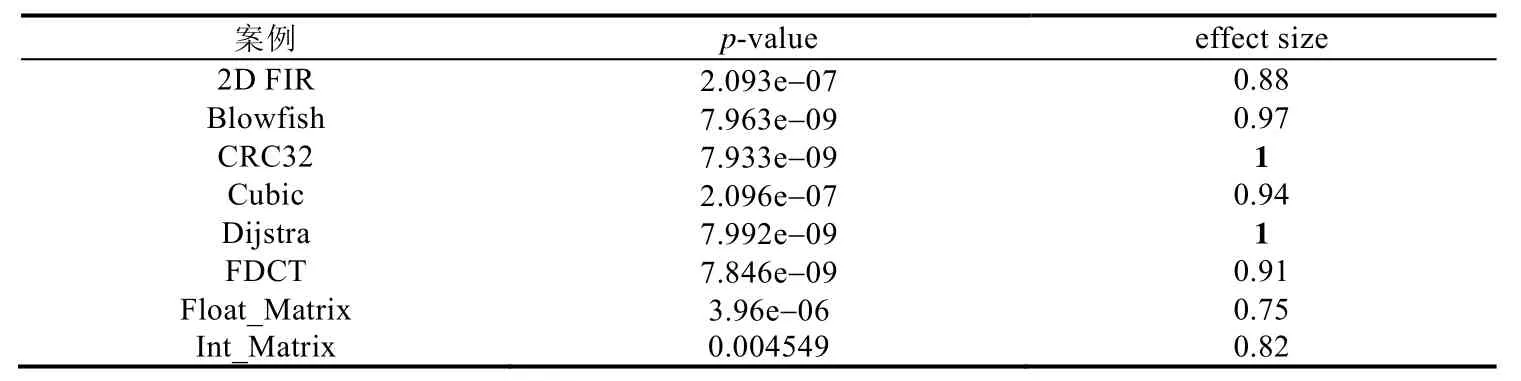
Table 11 Rank sum test results of energy consumption improvement percentageIΔeng% of GA-FP compared with Tree-EDA under 8 cases表11 GA-FP较之Tree-EDA在8个案例下能耗改进百分比(IΔeng%)的秩和检验结果

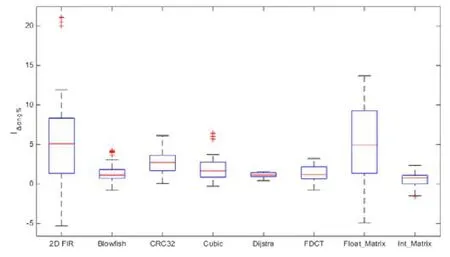
Fig.6 Boxplot using energy consumption improvement percentageIΔeng% of GA-FP compared with Tree-EDA图6 GA-FP较之Tree-EDA在8个案例下能耗改进百分比(IΔeng%)的统计盒图

Table 12 Statistical results of energy consumption improvement percentageIΔeng% of GA-FP compared with Tree-EDA under 8 cases表12 GA-FP较之Tree-EDA在8个案例下能耗改进百分比(IΔeng%)的统计量结果

(2) 问题2(收敛速度)的结果及分析

表13给出了在8个案例下收敛速度指标IΔi%(GA-FP达到不劣于Tree-EDA最优解对应最小迭代次数的相对减少百分比)的秩和检验结果.表13中第2列p-value值均小于置信水平0.05,表明在8个案例下,GA-FP的IΔi%指标在统计意义上显著优于Tree-EDA.表13中第3列的effect size值均大于等于0.8,说明GA-FP算法比Tree-EDA算法在大概率上具有更快的收敛速度.

从表14可看出,8个案例下的IΔi%指标平均值(GA-FP达到不劣于Tree-EDA最优解对应最小迭代次数的相对减少百分比)为34.5%,最大达到了83.3%.

图7所给出的统计盒图(GA-FP达到不劣于Tree-EDA最优解对应最小迭代次数的相对减少百分比)也直观地得到一致结论.

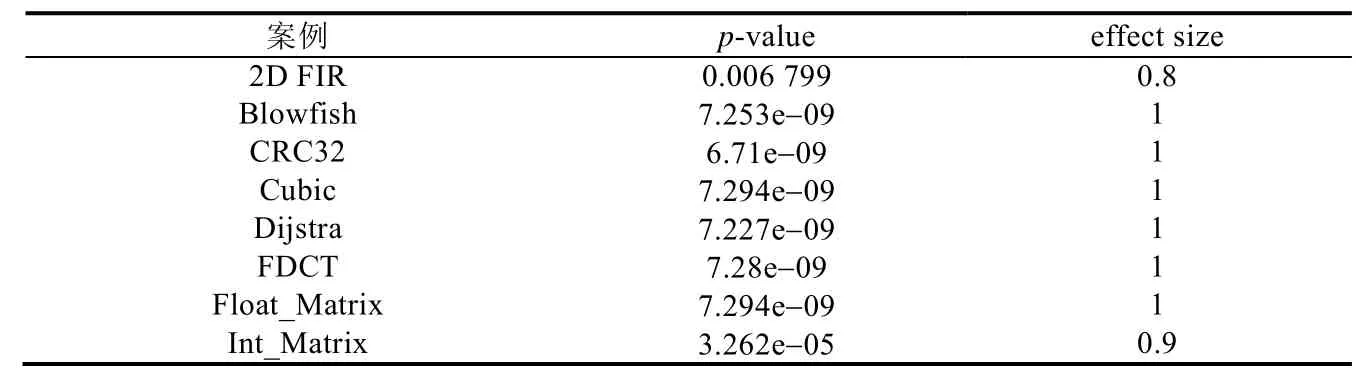
Table 13 Rank sum test results of the convergence speed metricIΔi% in 8 cases表13 在8个案例下收敛速度指标IΔi%的秩和检验结果

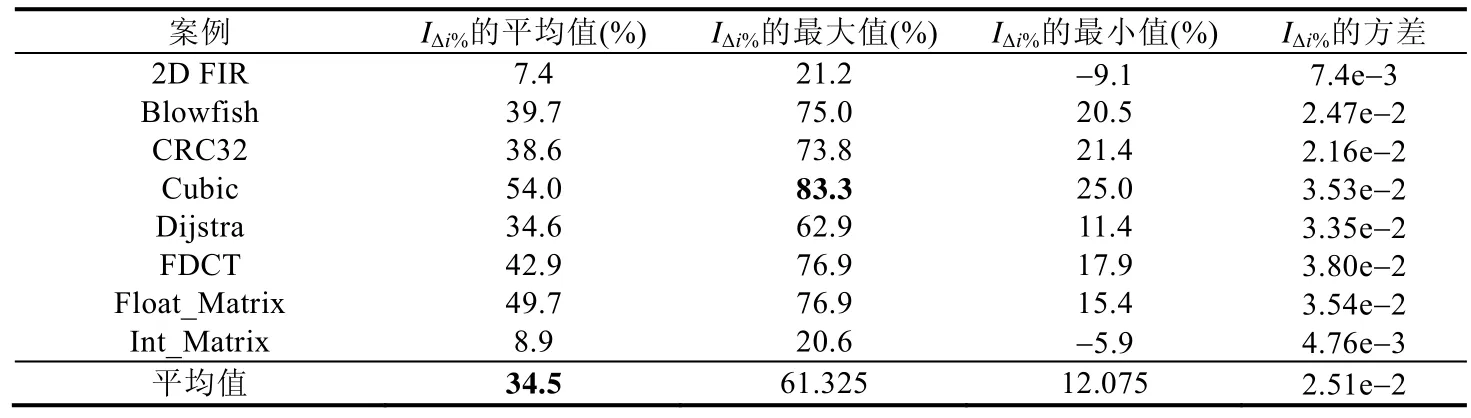
Table 14 Statistical results of convergence speed metricIΔi% in 8 cases表14 在8个案例下收敛速度指标IΔi%的统计量结果

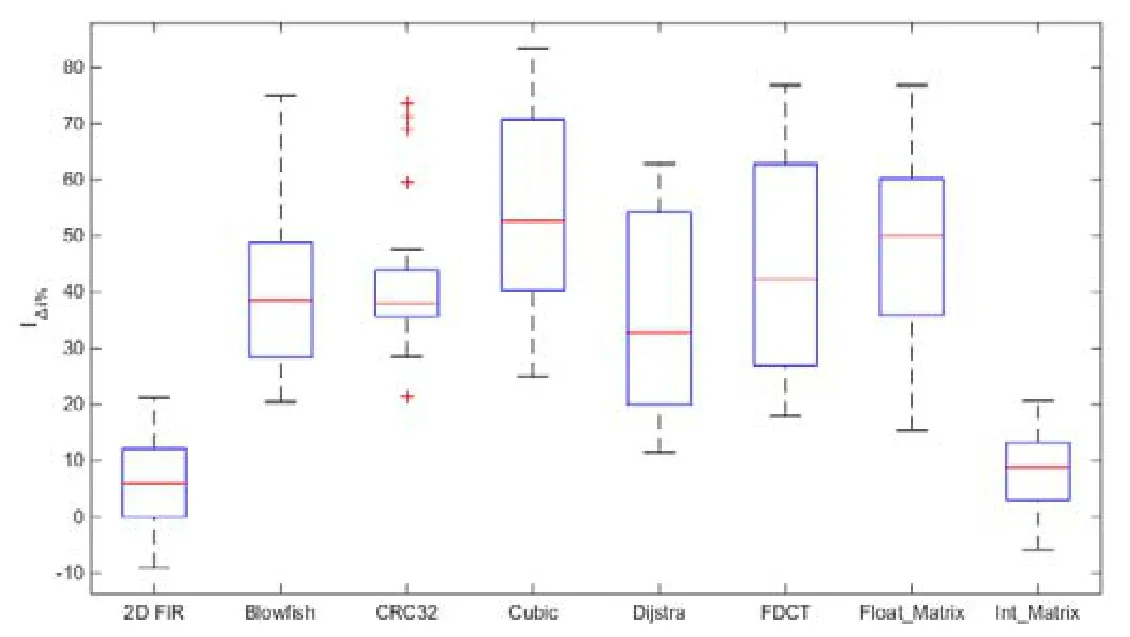
Fig.7 Boxplot using convergence speed metricIΔi% under 8 cases图7 收敛速度指标IΔi%的统计盒图

(3) 问题3(最优解中编译选项的正相关性)的结果及分析

表15给出了在8个案例下,Tree-EDA和GA-FP算法获得的最优解中编译选项正相关性指标IPC%(正相关编译选项在最优解中所占的比例)的秩和检验结果,表15中第2列p-value值均小于置信水平0.05,表明在8个案例下,GA-FP的IPC%指标在统计意义上显著优于 Tree-EDA.除了 Blowfish、Cubic和 Dijstra这 3个案例外,表15中第3列的effect size值均大于0.8,这表明与Tree-EDA算法相比,GA-FP算法获得最优解中的各编译选项之间在大概率上具有更强的正相关性.

表16给出了在8个案例下,Tree-EDA和GA-FP算法获得的最优解中编译选项正相关性指标IPC%(正相关编译选项在最优解中所占的比例)的统计结果.从表16可以看出,GA-FP算法的IPC%指标在8个案例下的平均值和最小值均优于Tree-EDA算法;仅在Cubic和Blowfish案例下,IPC%指标在最大值上GA-FP算法分别劣于和等于 TreeEDA算法.图8所给出的统计盒图也直观地得到一致结论.该实验结果说明:相比于 Tree-EDA算法,在GA-FP算法获得最优解中,各编译选项之间存在更强的正相关性.进而实证了文中在频繁模式集基础上引入“增添”和“删减”两种变异算子的有效性.

Table 15 Rank sum test results of positive correlation metricIPC% in the optimal solutions under 8 cases表15 在8个案例下最优解中编译选项正相关性指标IPC%的秩和检验结果

Table 16 Statistical results of positive correlation metricIPC% in the optimal solutions under 8 cases表16 在8个案例下最优解中编译选项正相关性指标IPC%的统计量结果

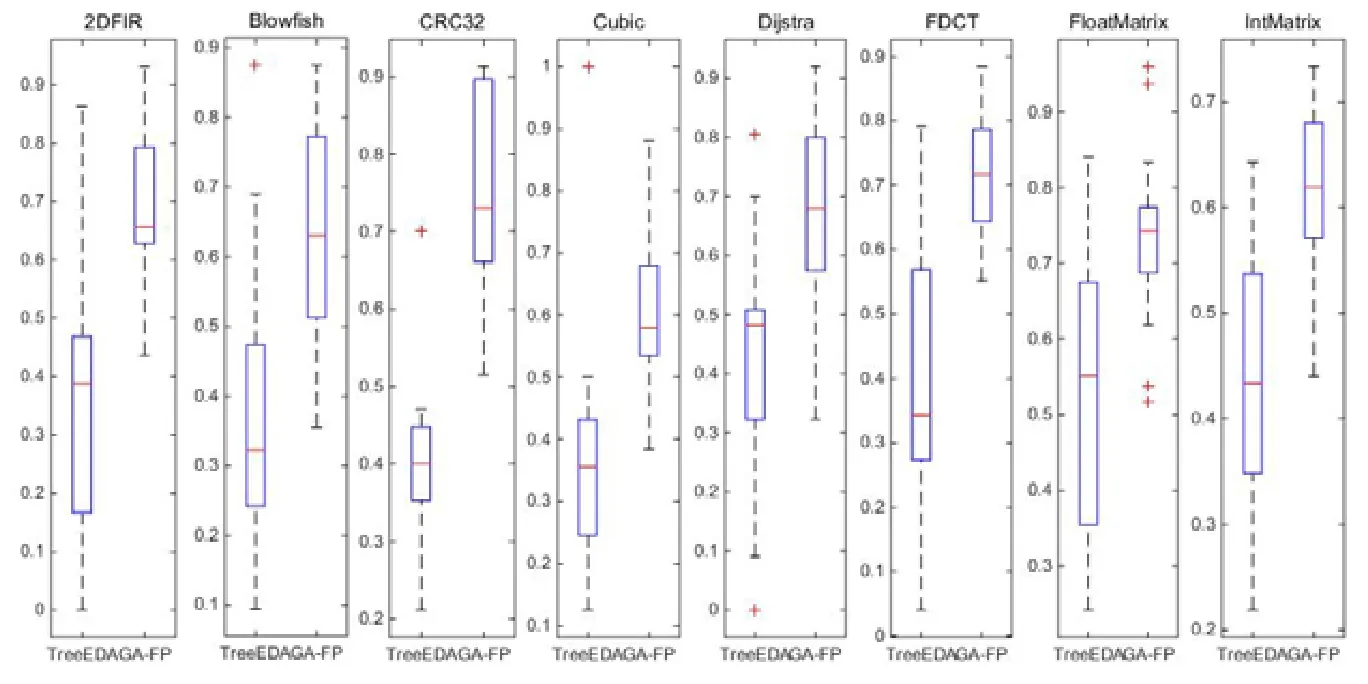
Fig.8 Boxplot using positive correlation metricIPC% in the optimal solutions under 8 cases图8 在8个案例下最优解中编译选项正相关性指标IPC%的统计盒图

(4) 问题4(编译选项的使用频度)的结果及分析

图9给出了8个案例在以能耗为优化目标下,每个GCC编译选项的使用频度情况.图9横轴中的数字表示编译选项的编号;而纵轴则通过不同颜色标识出不同案例下各编译选项的使用频度,并通过累加各案例中每个编译选项的使用频度得出度量指标Ifq%(xi)的值.横轴中所有编译选项编号按照Ifq%(xi)的值从左向右降序排列.从图9可以看出,在8个案例中,-freorder-blocks(43号)、-fschedule-insns2(47号)以及-fgcse(39号)依次为使用频度最高的 3个编译选项;而-falign-functions=0(29号)、-fno-reorder-blocks-and-partition(34号)和-fexpensiveoptimizations(38号)依次为使用频度最低的3个编译选项.

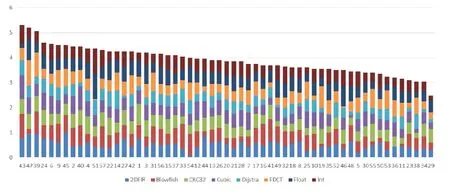
Fig.9 Histogram using the frequency metricIfq%(xi) of each compilation option under 8 cases图9 在8个案例下各编译选项使用频度指标Ifq%(xi)的柱状图

6 总结和未来工作

本文将频繁模式挖掘和启发式变异引入到传统遗传算法,提出一种用于GCC编译时能耗优化的算法GAFP.该算法通过考虑多个编译选项之间可能存在的相互影响,并在演化过程中使用频繁模式挖掘方法找出一组出现频度高且能耗改进幅度大的编译选项.在此基础上,进一步设计了“增添”和“删减”两种新的变异算子.通过案例研究,实证了 GA-FP的解质量和收敛速度在统计意义上显著优于 Tree-EDA;最优解中编译选的相关性分析,进一步验证了所设计变异算子的有效性.

本文在利用频繁模式挖掘时仅考虑对能耗有改进效果的编译选项组合,未涉及那些对能耗改进有负影响的编译选项集合,未来工作将综合考虑这些编译选项集合进一步优化现有的算法.另外,当前的优化算法在进行能耗评估时仍存在耗时长的问题,未来拟引入代理模型帮助解决这一问题.