时间周期线性扰动系统零解的稳定性分析

李 卓， 李 霞

（苏州科技大学 数理学院，江苏 苏州 215009）

稳定性理论是研究时间趋于无穷时微分方程解的性态，它在自然科学、工程技术、环境生态、社会经济等方面有着广泛的应用[1]。线性系统的稳定性问题较容易讨论，也是研究一般非线性系统稳定性的基础。常系数线性系统具有两个基本特征：系统是定常的、线性的。由于这两个特点，常系数线性系统的稳定性几乎可用线性代数的工具进行处理。关于常系数线性扰动系统零解稳定性的相关结论如下：

令

其中ai，j是实数（i，j＝1，2，…，n），x＝（x1，x2，…，xn）T∈Rn。

定理1[2]设f（t，x）在I×U 上连续，关于x 满足Lipschitz 条件，且对t 一致地有

非自治线性系统零解的稳定性比较复杂。在这方面的主要研究方法是根据系统的特征构造相应的Liapunov 函数（v 函数）：如用“类比方法”给出了一类非线性自治系统的Liapunov 函数，得到方程解渐近稳定的充要条件[3]；利用一般分离变量型v 函数，证明了一般高维非线性自治微分方程组解的全局稳定性和不稳定性定理[4]。对于非线性自治系统的扰动系统，借助于K 类函数的相关结论，提出了控制函数对的概念，在此基础上，讨论其零解的稳定性问题[5]；或是研究未扰系统或特殊扰动系统，如研讨若干扰动微分系统的Lipschitz稳定性和指数渐近稳定性[6]。用矩阵的Lozinskii 测度的方法，得到线性常微分方程系统的某些稳定性准则，导出了关于线性系统=A（t）x 稳定性的充要条件[7]；对于周期变系数常微分方程组描述的动力系统，建立了稳定性分析的Liapunov 指数的判别准则[8]。对微分方程零解稳定性的研究极其广泛，也有着重要的应用[9-11]。

笔者对周期线性扰动系统的零解稳定性进行研究， 是对常系数线性扰动系统零解稳定性研究的推广。文中主要结论是：在一定条件下，当周期线性扰动系统的扰动项是关于||x||的高阶无穷小时，周期线性扰动系统与未扰动系统的零解具有相同的稳定性，而且将这个结论应用于某一类具体的周期线性扰动系统中，取得了较好的结论。

1 主要结论

先考虑周期线性系统

其中A（t）＝（aij（t））n×n，满足A（t+T）＝A（t），是以T 为周期的连续周期函数。记系统（2）的基本解矩阵为Φ（t）。

引理1[12]存在非奇异可微周期矩阵P（t），以及一个常数矩阵Q，使Φ（t）＝P（t）eQt。

证明容易验证Φ（t+T）也是系统（2）的一个基本解矩阵，所以有非奇异的常数矩阵C，使Φ（t+T）＝Φ（t）C。令Q 是满足eQT＝C 的常数矩阵，再取P（t）＝Φ（t）e-Qt。由于P（t）是基本解矩阵Φ（t）和指数矩阵e-Qt的乘积，所以P（t）是可微的非奇异矩阵，且P（t）满足

作变量替换，x＝P（t）y=Φ（t）e-Qty，由于

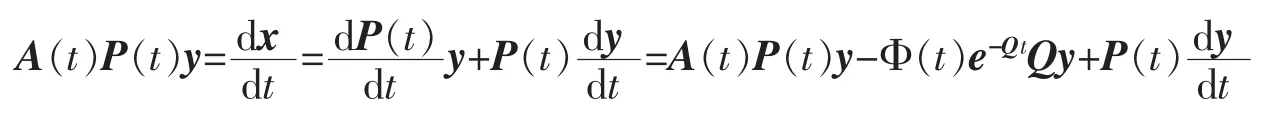
故新变量满足的方程组为

即将系统（2）零解的稳定性问题转化为线性常系数系统（3）零解的稳定性问题。

定义1非奇异的常值矩阵C＝eQT的特征值λ1，…，λn称为系统（2）的特征乘数，而把矩阵Q 的特征值ρ1，…，ρn称为系统（2）的特征指数。

引理2[2]若矩阵Q 的所有特征值均具有负实部，则系统（3）的零解渐近稳定；若Q 的所有特征指数均具有非正实部，且其具有零实部的特征值仅对应单重初等因子，则系统（3）的零解是稳定的；若矩阵Q 有正实部的特征指数，或有对应多重初等因子的零实部，则系统（3）的零解是不稳定的。

引理3[2]若矩阵A 的特征值λi均满足λi+λj≠0（i，j＝1，2，…，n），则对任意的实对称矩阵H，存在唯一的实对称阵B 满足ATB+BA=H，其中AT表示A 的转置。

对于周期线性扰动系统

其中A（t）＝A（t+T），f（t，x）＝f（t+T，x），将用经典的Liapunov 函数构造法研究其零解的稳定性。在此之前，给出两个零解稳定性的判别定理。

引理4[1]若有原点的邻域U 以及正定函数V（x），使得沿系统轨道的全导数（x）负定，则该系统的零解渐近稳定。

引理5[2]若有原点的邻域U 以及正定函数V（x），使得沿系统轨道的全导数（x）满足（x）＝λV（x）+W（x），其中λ＞0，W（x），且V（x）不是半负定的，则该系统的零解是不稳定的。

定理2设f（t，x）在I×U 上连续，关于x满足Lipschitz条件，关于t连续。若对于任意t满足则当系统（2）的特征指数没有零实部的特征值时，系统（4）的零解和系统（2）的零解具有相同的稳定性。

证明做变量替换x＝P（t）y ＝Φ（t）e-Qty（Φ（t）为系统（2）的基本解矩阵，P（t）为非奇异可微周期矩阵），由于

故新变量满足的方程组为

若系统（2）的零解渐近稳定，由于x＝P（t）y，其中P（t）是非奇异的可微周期矩阵，||P（t）||在（-∞，+∞）上都是有界的，则系统（3）的零解渐近稳定。由引理2，Q 的特征值均有负实部。由引理3，对n 阶单位矩阵E，存在唯一的矩阵B，满足方程QTB+BQ=-E。容易证得V（y）＝yTBy 必是正定的。

将V（y）＝yTBy 沿系统（5）求全导数，可得

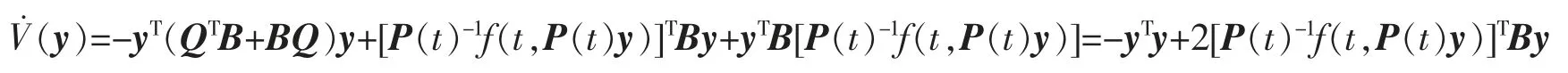
若系统（2）的零解不稳定，由于x＝P（t）y，其中P（t）是非奇异的可微周期矩阵，||P（t）||在（-∞，+∞）上都是有界的，则系统（3）的零解不稳定。由于Q 的特征值没有零实部，由引理2，Q 的特征值中至少有一个为正实部，设为λ0，Reλ0>0。因此，可选取常数α>0 使得A-（α/2）E 的所有特征值满足引理3 的假设，所以，存在唯一的矩阵B，满足方程（A-α/2E）TB+B（A-α/2E）＝E。

令V（y）＝yTBy，沿系统（5）求全导数得

同上，可证得对ε>0 有δ>0，当||y||<δ 时一致地有

所以当系统（2）的特征指数没有零实部的特征值时，系统（4）的零解和系统（2）的零解具有相同的稳定性。

2 定理的应用

在时间周期线性扰动系统中，因为增加了扰动项，在绝大多数情况下，无法求出其具体的解。下面的例子说明上述定理在高阶扰动系统中的一个实际应用。利用文中的定理，在不求出解的前提下，可以判断其零解的稳定性。

讨论微分方程组

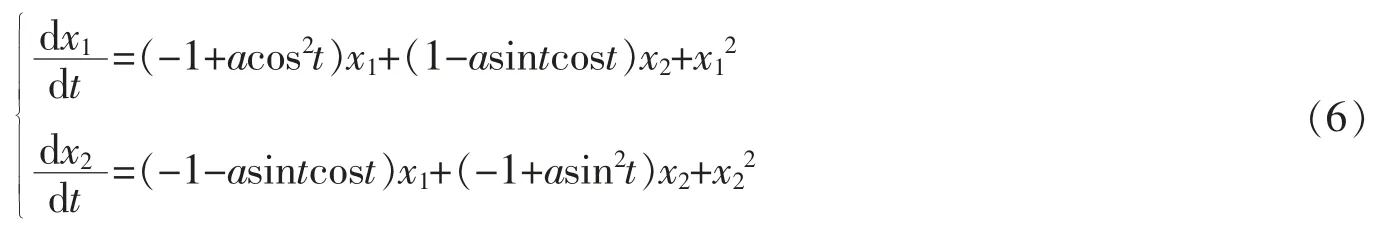
零解的稳定性。

解首先考虑

经过计算可求出方程组（7）的基本解矩阵为

Φ（t+2π）也是方程组（7）的基本解矩阵，且满足Φ（t+2π）＝Φ（t）C，所以

所以满足eQt＝C 的常数矩阵因为Q 的特征值为a-1，-1，所以当a＜1 时，方程组（7）的零解渐近稳定；当a＞1 时，方程组（7）的零解不稳定；当a＝1 时，根据定理2，方程组（7）的零解稳定性无法判断。

由于

由定理2，方程组（6）与方程组（7）的零解有相同的稳定性，即当a＜1 时，方程组（6）的零解渐近稳定；当a＞1时，方程组（6）的零解不稳定；当a＝1 时，根据定理2，方程组的零解稳定性无法判断。