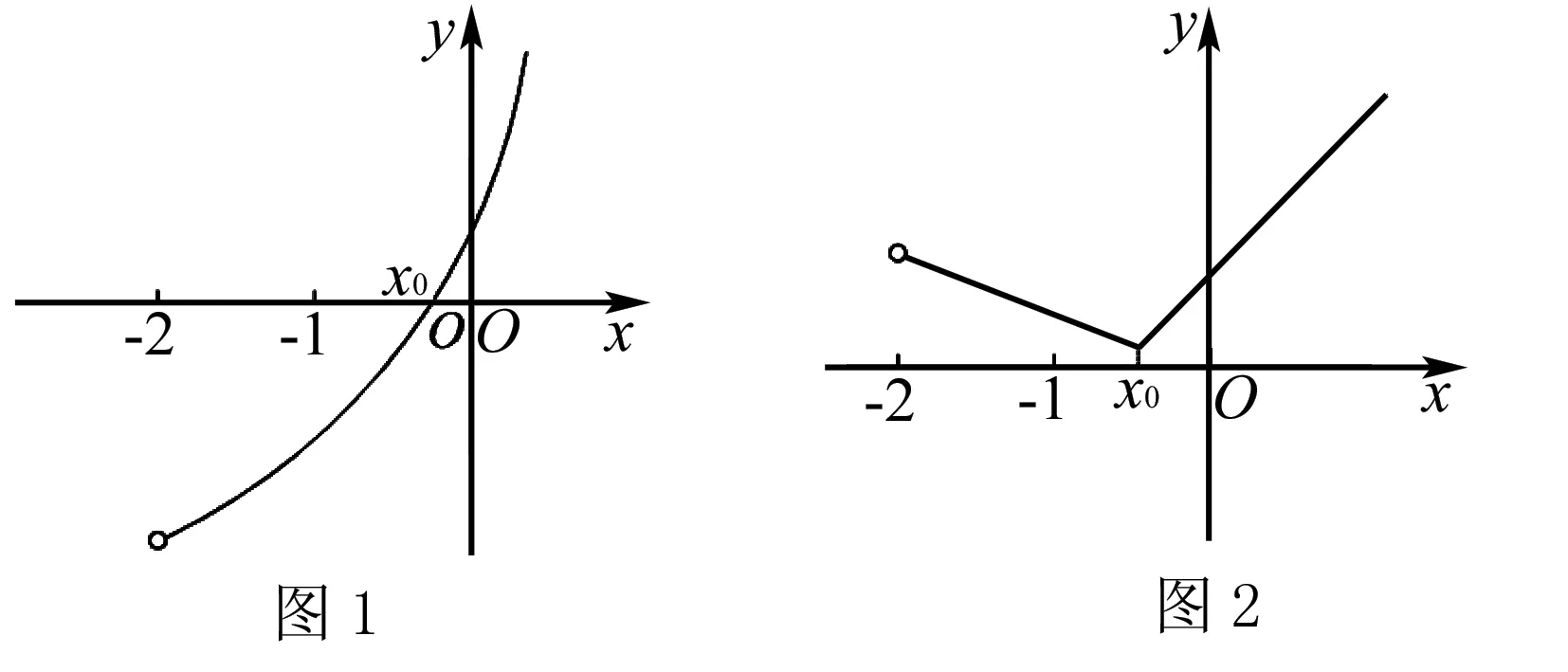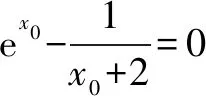构造函数证明不等式的数学思维途径
武增明
(云南省玉溪第一中学 653100)
不等式的证明,因其灵活多变、技巧性强著称.很多复杂的不等式证明,如果灵活构造函数,并利用导数,往往能获得简捷解决.而构造好相应函数是关键,从哪里入手,如何构造函数,怎么构造,构造函数的数学思维途径是什么,很多同学找不到突破口,感到无所适从,甚至构造不出合理的函数.下面就此问题作一些归纳、总结、探讨,以飨读者.
一、寻找待证不等式的等价不等式构造函数
找到待证不等式的等价不等式,观察等价不等式的结构,构造函数.
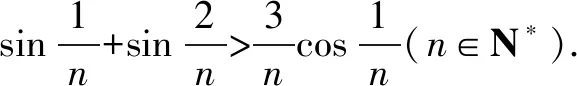
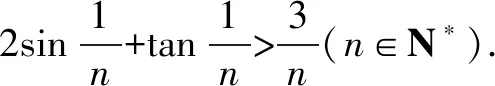
设函数f(x)=2sinx+tanx-3x(0 只需证明f(x)>0即可. 设函数g(x)=2cos3x-3cos2x+1,因为g(0)=0,且g′(x)=-6cos2xsinx+6cosxsinx=6sinxcosx(1-cosx)>0,因此g(x)>g(0)=0,即f′(x)>0,f(x)在区间(0,1]上单调递增,故f(x)>f(0)=0,不等式成立. 评注该问题的证明方法很多,此证法是通过构造函数f(x)=3x-x-1来证明不等式,可以说是很多证法中较为简单的一种证法. 若待证不等式中有多个变量,就选定一个为自变量,其余当作常数构造函数. 要证f(x)≥g(x),根据题设得f(x)-g(x)=h(x),由此把问题转化证h(x)≥0,从而想到构造函数F(x)=h(x). 例6 (2017年高考浙江卷·文22理22)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*).证明:当n∈N*时, (1)0 证明(1)略. (3)略. 先放缩后构造函数即对待证不等式中较为复杂的某一部分做放缩处理,使其变得较为简单,然后再构造相关的函数进行解题. 例7 (2013年高考全国新课标Ⅱ卷·理(21))已知函数f(x)=ex-ln(x+m). (1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明f(x)>0. 解(1)解略.m=1,f(x)在[-1,0]上单调递减,在[0,+∞)上单调递增. (2)f(x)的定义域为x>-m.当m≤2时,0 ∴g′(x)=0在(-2,+∞)上有唯一实根x0,如图1(是函数g′(x)的模拟图象),且x0∈(-1,0). ∴当x∈(-2,x0)时,g′(x)<0; 当x∈(x0,+∞)时,g′(x)>0. ∴g(x)在(-2,x0]上单调递减,在[x0,+∞)上单调递增,如图2(是函数g(x)的模拟图象),∴g(x)≥g(x0)=ex0-ln(x0+2). ∴g(x)>0,∴ ex-ln(x+m)≥ex-ln(x+2)>0. 综上,当m≤2时,f(x)>0. 通过以上例题,请认真体会基本要领,构造函数的数学思维,不论采用哪种方法构造函数,都需要我们在解题时细心观察与分析、类比联想与变形转化、自主探究与自我反思、合作学习与自我总结,尽量使所构造的函数易求导、易判导函数的符号.
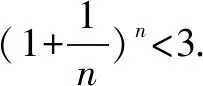
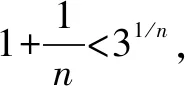
二、从多变量中选定一个为自变量构造函数
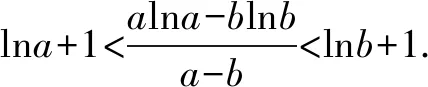
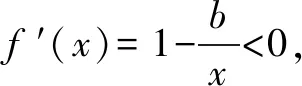
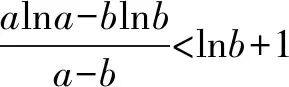
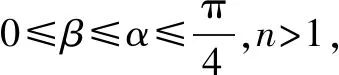
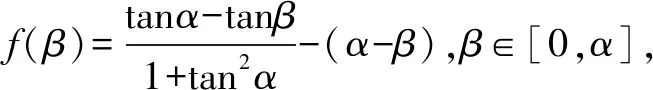
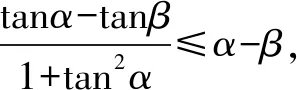
三、运用求数列的通项的方法构造函数
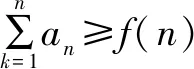
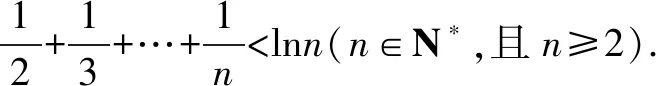
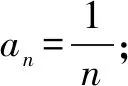

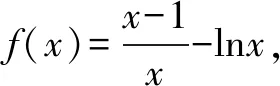
四、把不等转化为相等构造函数
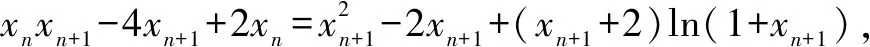
五、先放缩后构造函数