具有电导率补偿特性的低频电容土壤水分传感系统*

顾惠南,杨 雷,邓 霄,2*,吕华芳,宋志强,潘丽鹏,张 丽,崔丽琴

(1.太原理工大学物理与光电工程学院,太原 030024;2.太原理工大学新型传感器与智能控制教育部与山西省重点实验室,太原 030024;3.清华大学水利水电工程系水沙科学与水利水电工程国家重点实验室,北京 100084)

土壤水分含量是一项重要的土壤物理参数,水分含量检测对现代精准农业的研究具有重要意义。目前,常用的土壤水分检测方法有时域反射法(TDR)和频域反射法(FDR)两种。

TDR型传感器通过两个传感探头在土壤介质中发送和接收高频电磁波[1]。电磁波的传播速度随着土壤中介质的含水量差异而变化,从而实现水分检测。FDR型传感器的原理是将土壤介质作为等效电容[2],置于振荡电路中,检测输出的振荡信号[3],土壤含水量可以通过振荡频率信号的变化来获得[4]。TDR型传感器的采样频率通常在1GHz以上[5],FDR型传感器的检测频率约在30～10 MHz之间[6],较高的测量频率会提高传感器的电路成本,无法应对大规模布设的要求[7]。

然而,在低频情况下对土壤等效电容的检测会受到土壤盐分、孔隙大小等干扰因素的影响,单纯研究水分和电容的关系无法满足实际应用的精度要求。针对以上问题,我们提出了采用低频段电容检测土壤水含量,同时利用土壤电导率来修正电容和水分的关系的方法,以达到减小干扰因素影响的目的,实现低成本且满足精准农业测量精度要求的新型土壤水分传感器的设计。

1 基本测量原理

土壤水分传感器主要利用了水分、土壤、空气三种介质的介电特性差异的原理(水的介电常数为80,土壤的介电常数为2～9,空气的介电常数为1。因此,土壤中介电常数的变化可以反映出土壤中水含量的变化。土壤作为一种多孔介质,其相对介电常数εc在复数域内可表示为[8]:

εc=ε′-ε″j

(1)

式中:εc为复介电常数;ε′为介电常数的实部,主要受水分因素的影响;ε″为介电常数的虚部,受土壤中盐分、孔隙大小、土壤质地、测量频率,温度等因素影响[4,9],其中盐分影响较大。

由于电容传感探头与其内部的填充物质的介电常数有关,即

C=gεc

(2)

式中:C为电容传感探头的测量值;g是与传感探头规格、形状等因素有关的常数[8]。因此,可以通过对土壤中电容的检测实时反映出土壤介电常数的变化。

土壤电导率是主要反映土壤中盐分的物理参数[10],结合式(1)和式(2),在土样测量频率一定、温度和土样情况相似的情况下,可以通过电容及电导率的测量,较精确的得出水分的变化情况。

2 传感器的设计与应用

传感器的设计分为电容测量和电导率测量两部分,首先通过使用电容传感器的测量值拟合得出电容与水分值的关系,再利用所测电导率值修正电容水分关系,最终得出式(1)中所示的实部(水分影响)和虚部(电导率影响)的综合考虑结果,从而实现在低频测量情况下的土壤水分的高精度检测。

2.1 电容测量

本文所设计的土壤电容探头采用平行共面电容极板的设计,由于电容极板的测量范围受材料,规格,电极形状等因素影响[11],且当极板电容两端相邻表面积越大,极板间距越小时,电容传感器的变化范围越大,传感效果越好[12],因此我们采用了锯齿状的电容极板设计。设计结构图如图1所示。其中,保证极板厚度为均匀的0.6 mm以避免工艺造成的测量误差,电容测量值反映出该区域的土壤水分平均值。

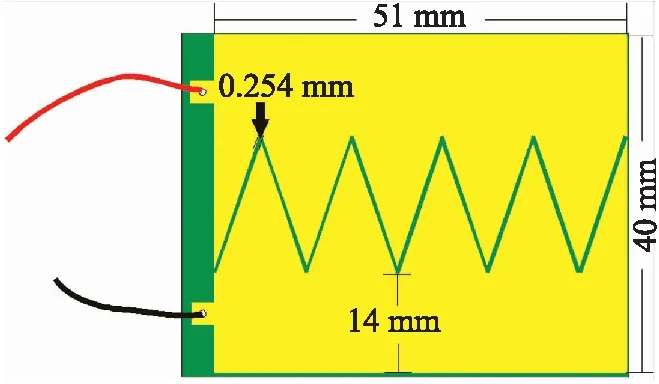
图1 电容传感探头结构图

对于电容的测量,大多数集成芯片不能提供很高的测量频率,但是,它们确实可以节省大量的成本。在本次研究中,选用恩智浦公司开发的电容式触摸传感芯片MPR121进行土壤水分检测。该芯片可提供恒定的充电电流I(A)(范围1 μA～63 μA),设定充电时间T(s)(范围0.5 μs～32 μs),同时芯片内部带有10位的A/D采集器,从而将电容值的测量转化为对电压信号的测量。测量原理图如图3所示。通过设定充电电流I(A),使得芯片对电容极板进行恒流充电,到达设定的充电时间T(s)时,对电压信号进行放大、滤波,通过内部的模数转换获得直接测量值ADC值,再通过I2C通信协议进行数据传输。

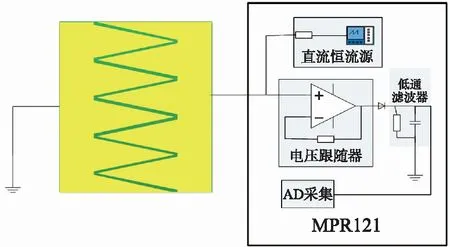
图2 电容检测原理图

测量值与测量电压值的关系如式(3):

(3)

式中:Vdd为芯片基准电压,U为输出电压。由电容的物理特性,可以得到其余充电电流,充电时间和电压的关系为:

(4)

根据式(3)和式(4)可以得出测量电容值的分辨率为:

(5)

由式(4)和式(5)分析可知,当I和T的乘积增大时,电容测量范围增大,而分辨率会变差,产生矛盾,因此对参数的选择进行了研究。分别对检测频率一定的情况下及I,T乘积一定情况下进行了分组实验,土壤中的水分值使用单位体积水分含量来确定(VWC),结果如图3所示。从图中可以看出,针对同一土样,当测量频率越大时,测量值受到充电电流等其他因素影响较小。因此,为了保证实验效果,测量频率的取值可以尽量增大。

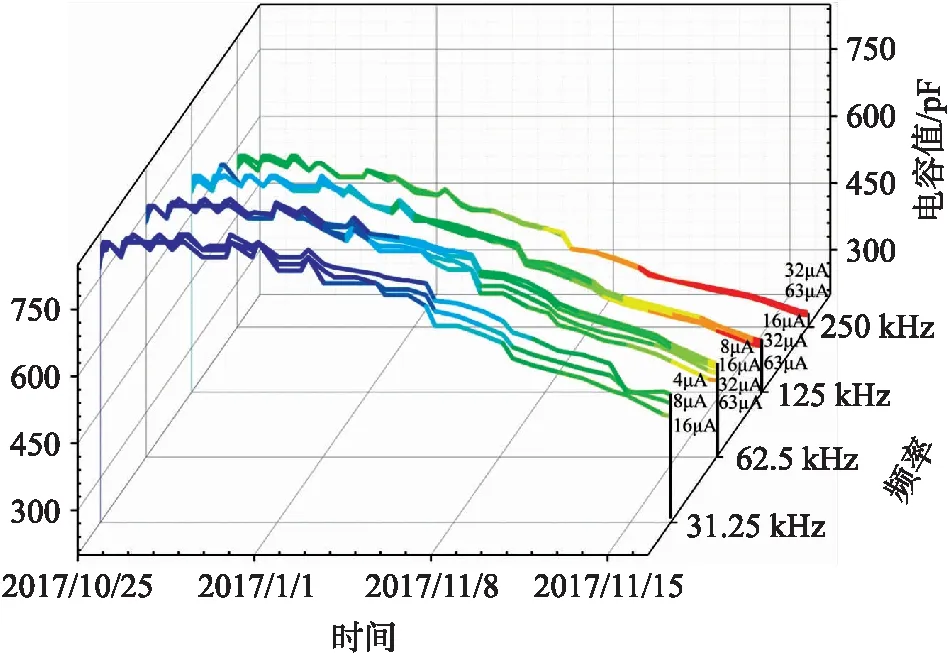
图3 相同频率下的电容测量情况

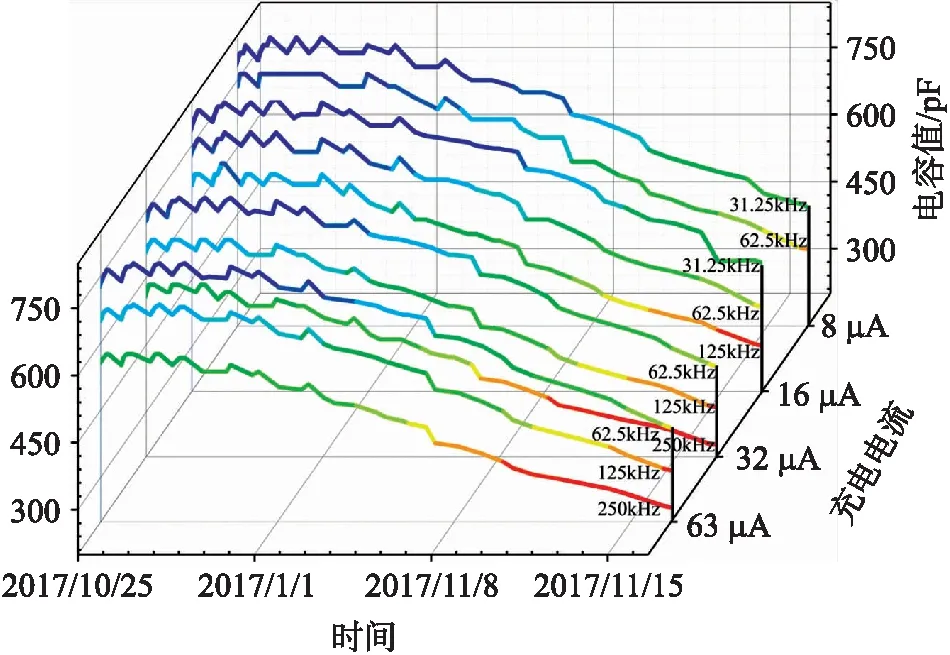
图4 不同充电电流条件下土壤样品在相同测量范围内的测试结果比较

当充电电流I与充电时间T的乘积设为一定时,实验结果如图4所示。从图中可以看出,电容的感应范围基本不变(约为350 pF),当T值一定时,I值增大,测量电容值总体减小,由式(5)可知,电容值越小,分辨率越高,因此传感器的I值尽量设大。由于电容对水分感应范围主要在200 pF～800 pF之间,由式(4)可知,I和T的乘积影响电容值的测量范围,因而综合以上各因素,选择设置测量参数I为63 μA,T为4 μs。

2.2 电导率的检测

电导率的测量使用二电极法进行检测。具体将两根金属探针置于土壤中,通过施加电压U,设置采样电阻R,形成回路[13],测量电路原理如图5所示。测量系统采用直流恒压源与传感触点、采样电阻串联,通过16位模数转换芯片ADS1100获得精确的电压采样值。针对采用直流电压源存在不可避免的电极极化现象的问题,在设计中利用了继电器的开关作用,减少电极的通电时间;另外,采用了10 MΩ的采样电阻R,从而减小回路电流,降低极化现象的影响。同时,传感探头采用紫铜材质的探针,相较于不锈钢、黄酮等材料,紫铜电极在插入土壤后建立比较稳定的电位所需的时间短,且电压波动小[14]。利用该原理可以得到所测土样电压值Us,如式(6)所示:

Us=E-Um

(6)

式中:Um为通过ADS1100获得的直接测量电压值,E为施加的直流恒压源电压。

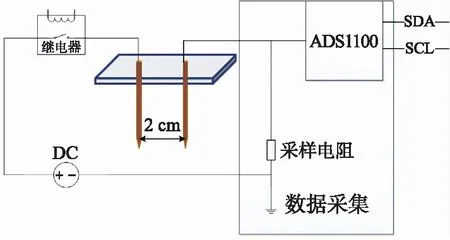
图5 电导率采集原理

实验中传感器的每次采样周期为5 s,通电时间为1 s,待测量数据稳定后进行读数。同时在稳定的室温环境下,将测量数据与意大利Hanna公司的手持电导率仪HI98331(分辨率1 μs/cm,自带温度补偿功能)对同一土样的测量数据采用幂函数(Allometric)模型进行数据拟合,结果如图6所示。

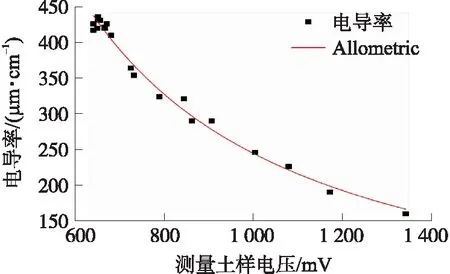
图6 测量土样电压和土壤电导率之间的关系

式(7)为利用幂函数模型拟合出的土样测量电压与电导率之间的函数关系,其校正决定系数R2为0.987 2,表明利用此探针测得的电压可以较好的反映电导率的变化情况。

(7)

3 水分校正模型

当土壤密度、温度等因素相同的情况下,土壤水分与土壤电导率、土壤等效电容值存在一定的数学关系。为了确定这一关系,从山西太原某地点(37°45′11″N,112°43′34″E)采集黄土样本,制作了两份密度为1.45 g/cm3的标准测试样品,用于持续测量其在土壤风干过程中等效电容和电导率的变化情况。为了得到标准的测试样本水含量变化情况,在实验中采用国际上通用的称重法[15]以及单位体积水分含量VWC(Volumetric Water Content)指标对土样情况进行判定,并利用式(8)进行计算:

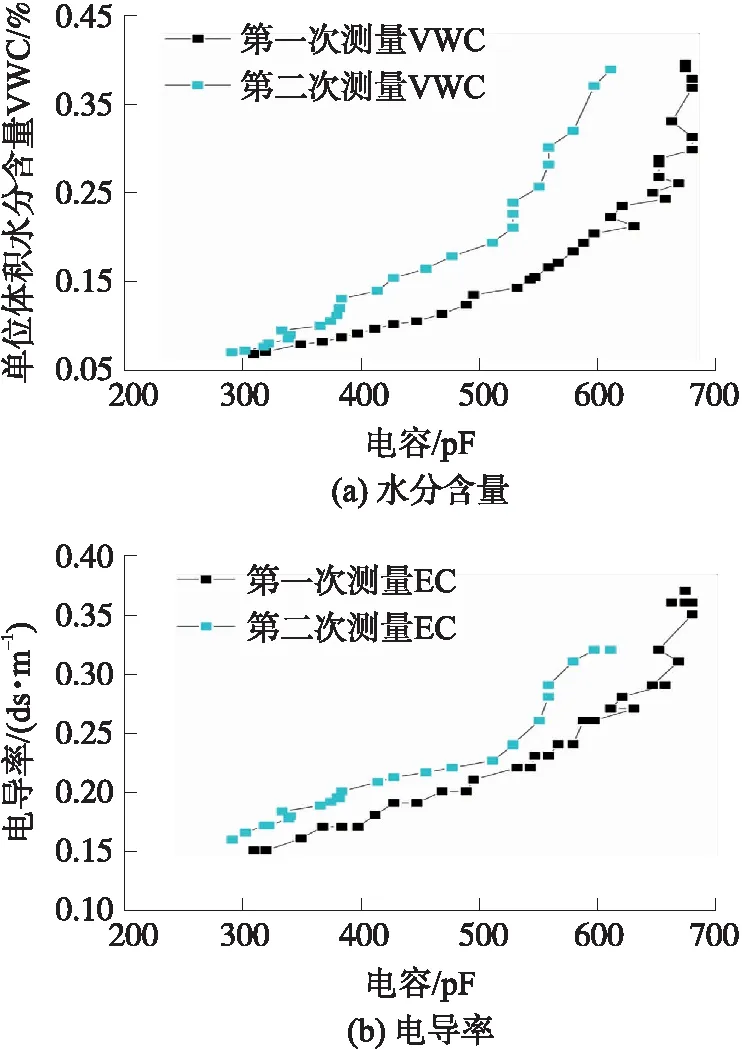
图7 两次土壤风干过程中的水分含量和电导率测量值情况对比

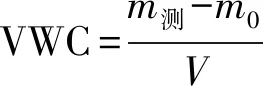
(8)

式中:m测为土样实时测量质量,m0为干燥样本土初值,V为样本罐体积(943 cm3)。图7为分别对两份土样测量数据进行对比的结果,图中蓝色测量点为第一份土样测量值,黑色测量点为第二份土样测量值。由式(1)可知,电容值反映复介电常数的变化,而土壤水分仅与复介电常数的实部相关,因此在相同电容值测量的情况下,电导率的变化值影响水分值。

我们采用以下方法对水分值进行校准:

θr=θ1=φ1(C)

(9)

θ2=φ2(C)

(10)

ECr=EC1=η1(C)

(11)

EC2=η2(C)

(12)

EC=EC-ECr

(13)

(14)

θ=θr+θc

(15)

式中:φ1、φ2分别为第一和第二组土样中电容与水分的关系,η1、η2分别为第一和第二组土样中电容所对应的电导率测量值。将第一组土样中的测量值作为测量基准值获得θr、ECr,在相同电容情况下电导率的差值与水分的差值存在比例关系如式(16),从而获得电导率影响的水分校正值θc,基准值θr与校正值θc的和即为水分标准测量值θ。综上,当对未知土样进行检测时,需要准确的测量值电容C,电导率EC,并确定函数φ1,η1,φ2,η2。化简:

(16)

采用Logistic模型[10]对两次测量数据进行拟合以获得经验公式,数据拟合情况如图8所示。

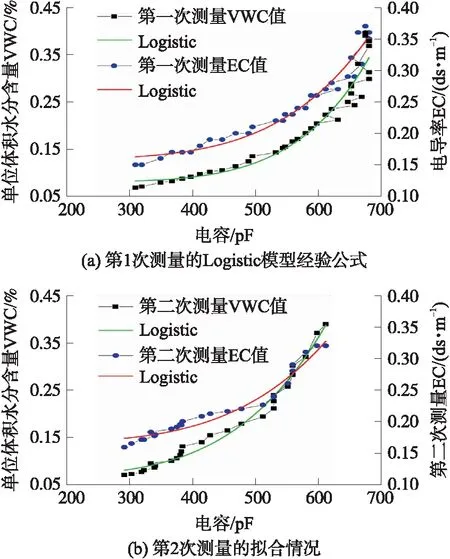
图8 两次测量情况的Logistic模型数据拟合

图8(a)为第一次测量的Logistic模型经验公式,图8(b)为第二次测量的拟合情况,故能够根据拟合情况得出经验式(17)～式(20):

(17)

(18)

(19)

(20)

将以上所得4个公式再带入式(18),可以得到最终的水分校正模型式(21)。

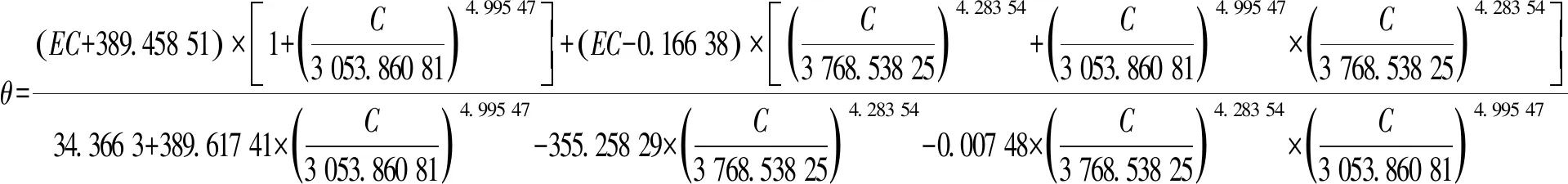
(21)

4 实验过程与结果分析

为了验证上述水分校正模型准确性,重新制作3罐土壤样本并分别于2017年11月21日至2017年12月13日,2017年12月19日至2018年1月9日,2018年1月23日至2018年2月9日,完成三次土壤吸水风干实验,并分别对土壤水分含量情况进行抽样检测。三次实验的测量值包括电容、电导率和利用烘干法测得的标准单位体积含水量如表1所示。

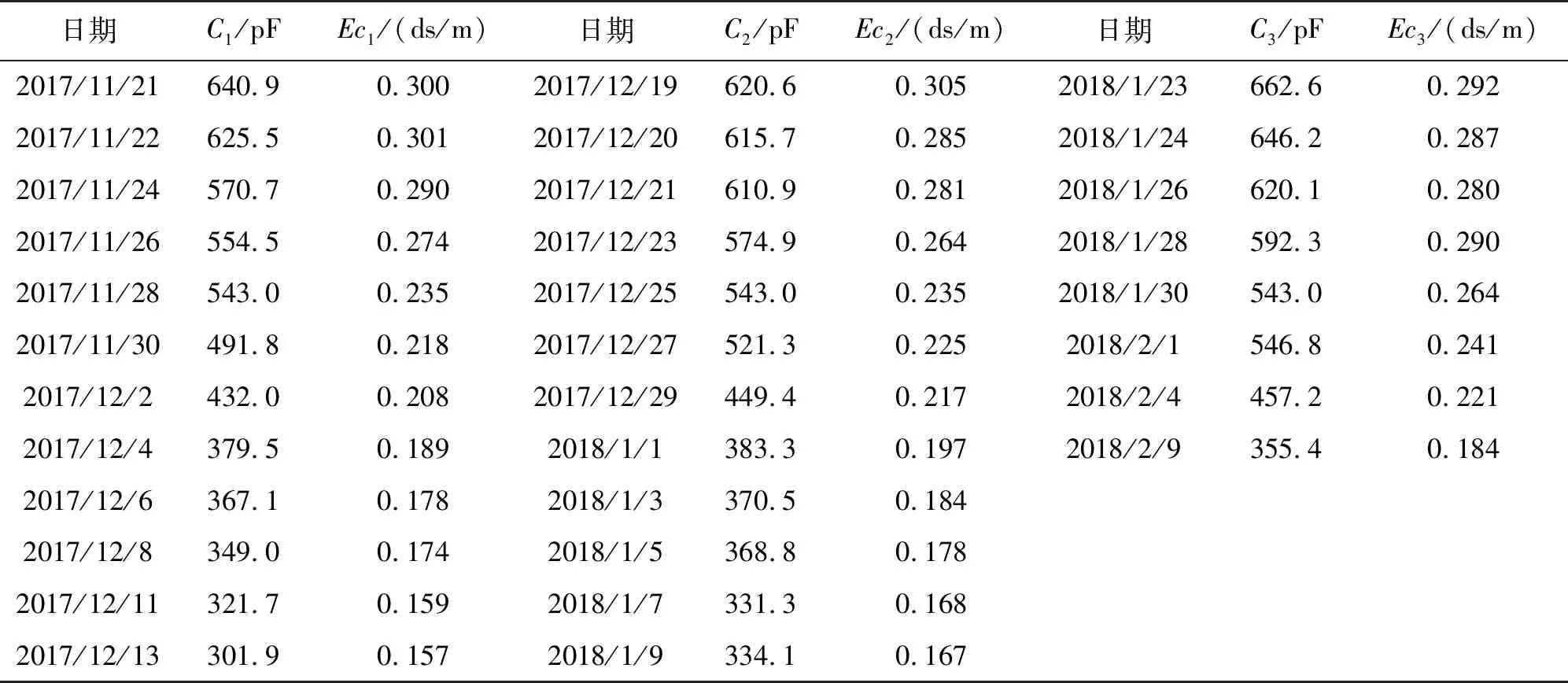
表1 3次土样风干过程测量参数

将三次测量值分别带入推导出的水分校正模型,并将计算得到的水分预测值与使用称重法得到的准确VWC值进行对比,结果如图9所示。从图中可以看出,三次测量的最大绝对误差分别为3.140%,2.549%,3.282%。

进一步使用平均绝对误差Mean Absolute Error(MAE)式(22)对传感器进行性能评估。

(22)

式中：n为实验次数,θi为每一个检测点的测量水分值,yi为相对应的标准土壤水分值。通过计算可以得出,三次测量的MAE值分别为1.549%,1.179%,1.228%,说明此传感器能够满足对于黄土土质的重复性测量要求,且最大误差小于3.3%。

5 结论

本文通过电导率的校正,设计了一款能够适应在低频段进行检测的电容土壤水分传感器,采用集成电路芯片MPR121对比在不同充电电流、充电时间情况下的测量情况,选择出了最佳的测量参数。应用紫铜电极进行二端法电导率检测,将测量到的数据通过Logistic模型进行拟合获得经验公式,并计算得出利用电导率校正的电容水分关系。分别将同一土样的多次测量结果及不同土质的测量结果与标准称重法获得的标准水分值进行对比,结果表明,这种低成本的、具有电导率补偿功能的低频电容土壤水分传感器的最大绝对误差小于3.3%,平均绝对误差小于2.0%,能够满足农业生产对土壤水分检测的精度要求,且其低成本的特性更加适用于大范围多点的土壤水分检测系统,具有一定的现场应用价值。

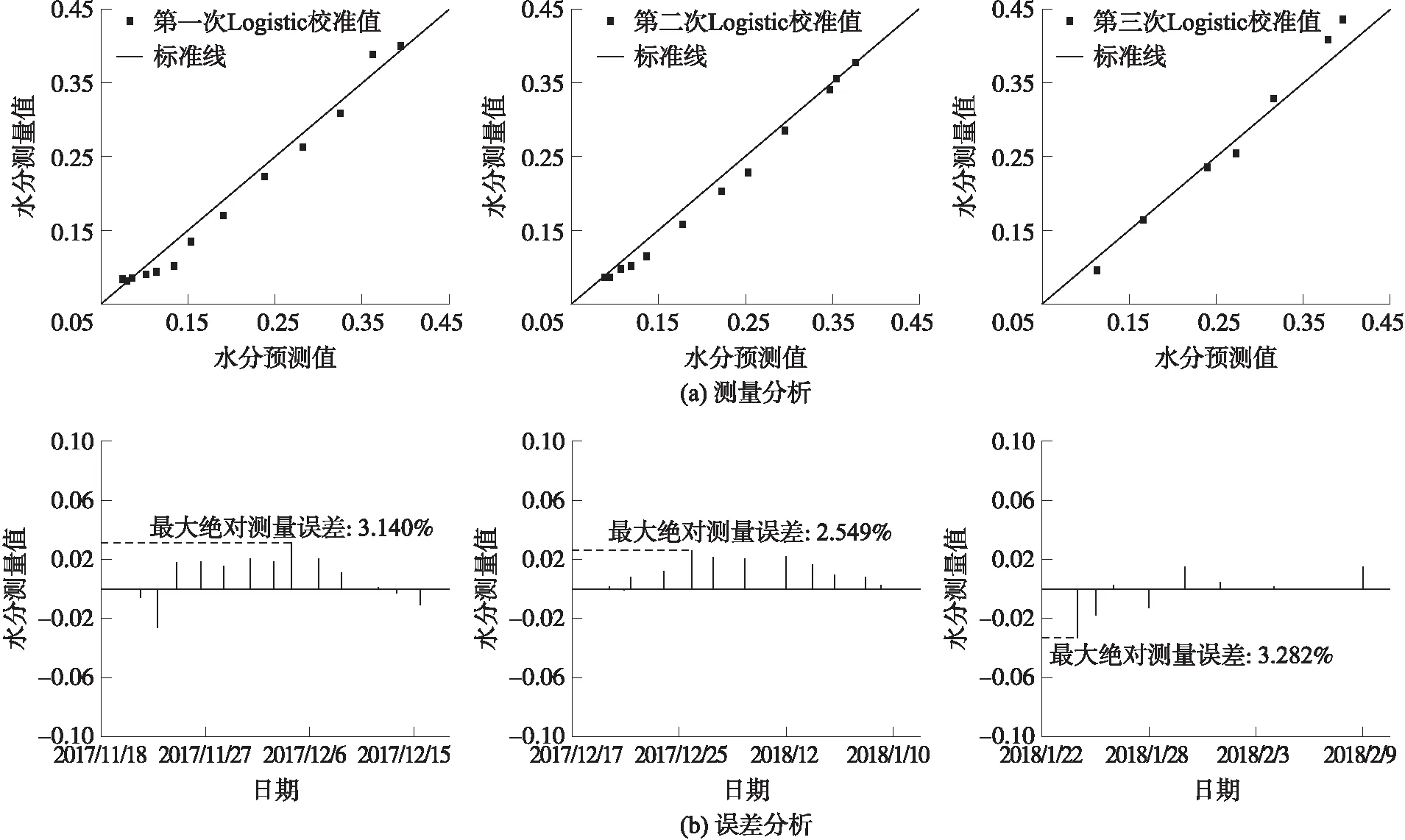
图9 3次测量值与实际值(称重法)对比(a)测量分析(b)误差分析