基于多传感器信息融合的自主跟随定位及避障方法*

王正家,夏正乔,孙楚杰,王 幸,李 明

(湖北工业大学现代制造质量工程重点实验室,武汉 430068)

自主跟随机器人被广泛的应用于工业、农业及日常生活等多个领域,在自由空间中对移动目标的精准定位是保证其跟随性能的关键,也是长期研究的重点。目前,主要的定位技术有视觉导航定位、GPS导航定位和声波定位等[1-3]。其中视觉导航定位技术通过识别特征标识实现定位,不仅算法复杂,而且易受环境影响从而丢失目标[4-5];GPS导航定位受场地影响较大,在室内或者城市建筑之间,GPS信号容易丢失,不适用于自由空间[6];声波定位技术主要采用超声波定位,对场地要求较低,且不会被光照等环境因素影响,因此它适合用于自主跟随机器人的定位。文献[7-9]在移动目标上用单一超声波信号源发射超声波信号,在自主跟随机器人上接收超声波信号,从而确定移动目标位置,虽然能实现定位,但是由于超声波传感器发射角度小,自主跟随机器人很容易进入超声波信号盲区,导致跟随失败,并且该方法不能检测移动目标实时移动姿态;当自主跟随机器人遇到障碍时,只检测障碍物距离,不检测障碍物方位,自主跟随机器人避障时可利用信息较少。

因此,针对上述问题,本文提出了一种基于多传感器信息融合的自主跟随定位及避障方法,该方法通过在移动目标上增加多信号源,使自主跟随机器人与移动目标之间建立冗余信道,弥补单一信号源发射角度小的问题;利用三角定位法测量信号源坐标,并通过最小二乘逼近计算移动目标中心位置;对信号源进行编号,根据测量出的信号源位置、移动目标中心位置和信号源编号,计算移动目标实时移动姿态;在自主跟随机器人上设置测距模块,当自主跟随机器人丢失信号源信号时,能够根据测距模块的信息保持跟随。实验结果验证了该方法的有效性。

1 移动目标的基本定位方法

三角定位法是一种常见的测量物体的距离和方位的方法[10],其原理图如图1所示。已知A、B的坐标分别为(-a,0)、(a,0)以及被测物M相对于A、B的距离la、lb,计算出M当前的坐标(x,y)及M到A、B中点O的距离d和方向偏角θ。

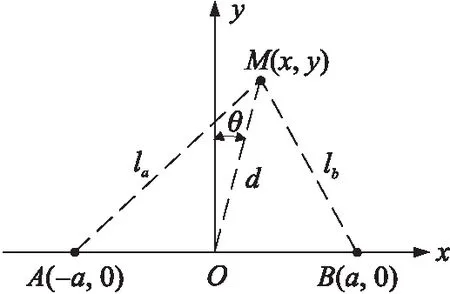
图1 三角定位法

由几何关系可知:

(1)

可得出M点坐标:

(2)

(3)

M的定位特征数据d、方向偏角θ分别为:

(4)

θ=arctan(y/x)

(5)

在工程应用中,通常在被测物M上设置信号源,在测量物的A,B处设置信号接收节点,信号接受节点A,B接收到信号源M发射的信号后,便可计算出距离la、lb,从而计算出M当前的坐标(x,y)及M到A、B中点O的距离d和方向偏角θ。

2 多信号源定位及避障模型

本论文设计的多信号源定位模型原理图如图2所示。将N个信号源Mi(i=1,2,3,…,N)布置在移动目标上,这些信号源在以移动目标中心点M为圆心、R为半径的圆上等角度均匀分布;在跟随机器人上布置信号接收节点A、B和测距模块C、D、E,其中测距模块C、D分别与信号接收节点A、B邻近,测距模块E布置在A、B中点O处。

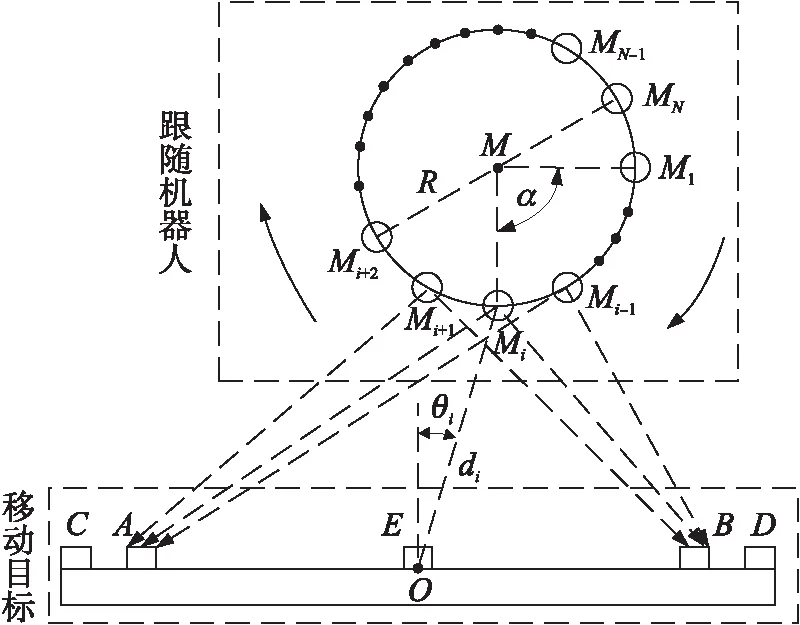
图2 多传感器信息融合定位模型

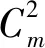
3 多信号源定位及避障算法

为了具体的计算出移动目标中心坐标M(x,y)、距离d、方向偏角θ和实时移动姿态,并且在遇障时自主跟随机器人能正确的调整运动速度和方向,本文根据上述多信号源定位模型设计了多信号源定位算法。该方法分为计算移动目标中心坐标及特征数据、计算实时移动姿态和遇障分析。

3.1 计算移动目标中心坐标及特征数据

通过从信号源M1开始,到信号源MN发送信号完成截止,以顺时针的方向依次进行信号源切换,获得信号源Mi(i=1,2,…,N)的坐标和特征数据di和θi。对于任意两个信号源Mj和Mk可以求出对应的移动中心位置Mojk及其特征数据(距离dojk和方向偏角θojk),其原理图如图3所示。

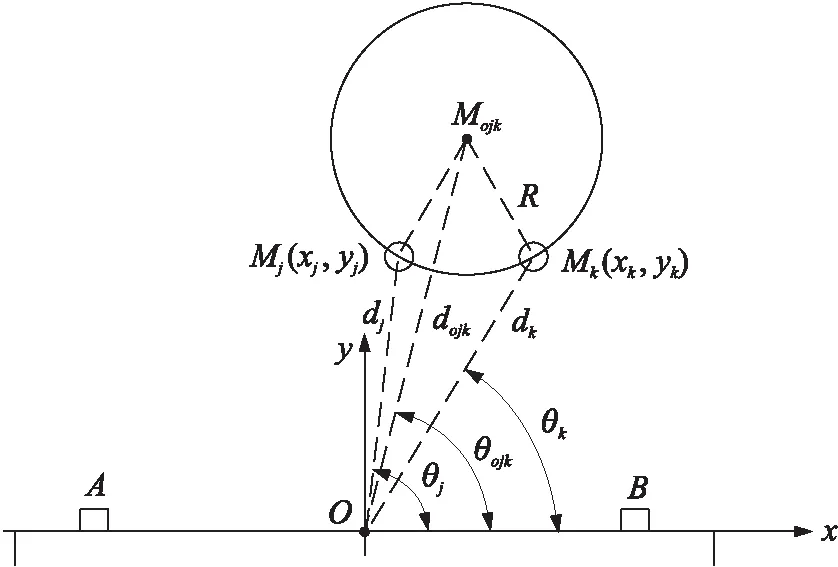
图3 中心位置Mojk计算

图中Mj(xj,yj)、Mk(xk,yk)分别表示信号源Mj、Mk的坐标,其中j>k。设Mojk的坐标为(xojk,yojk),由几何关系可知:

(6)

由式(6)算出的Mojk的坐标(xojk,yojk)有两个,并不能确定移动中心位置。本文使用向量叉积[11]的方法来确定移动中心位置。用MojkMj表示由Mojk到Mj的向量,用MojkMk表示由Mojk到Mk的向量,则MojkMk×MojkMj的行列式为:

(7)

由于信号源是顺时针编号排布的,则:

(8)

即:

(xk-xojk)(yj-yojk)-(xj-xojk)(yk-yojk)<0

(9)

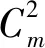
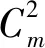
(10)

(11)

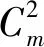
3.2 计算实时移动姿态

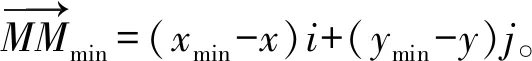
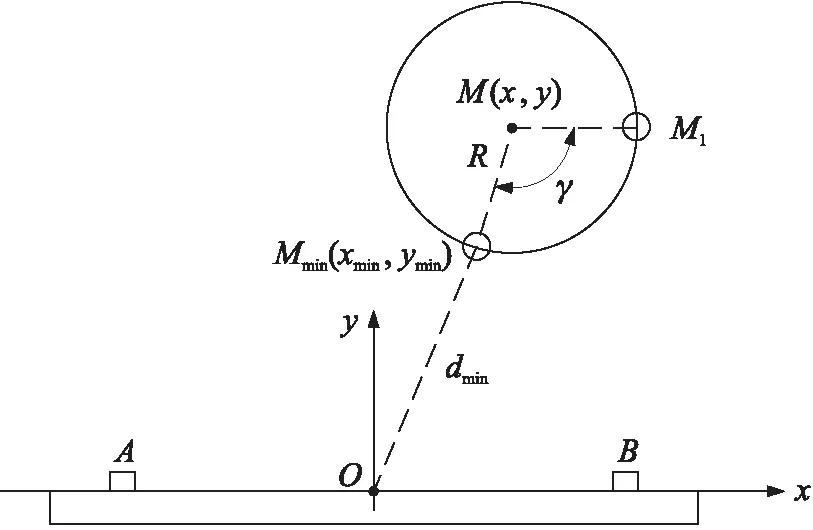
图4 移动姿态计算

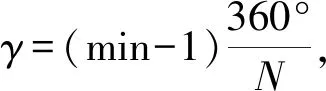
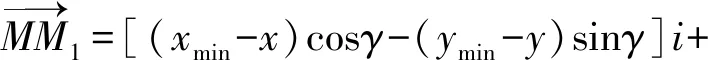
(12)

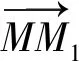
3.3 遇障分析

当信号源由M1到MN切换发送信号完成后,信号接收节点A、B都没有接收到任意信号源的信号或者其中一个信号接受节点没有接收到任意信号源的信号,自主跟随机器人将会启动测距模块C、D、E,测距模块会进行测距,根据测距结果,自主跟随机器人重新调整运动速度和方向。在自主跟随机器人与移动目标之间的障碍有如图5所示5种方式。

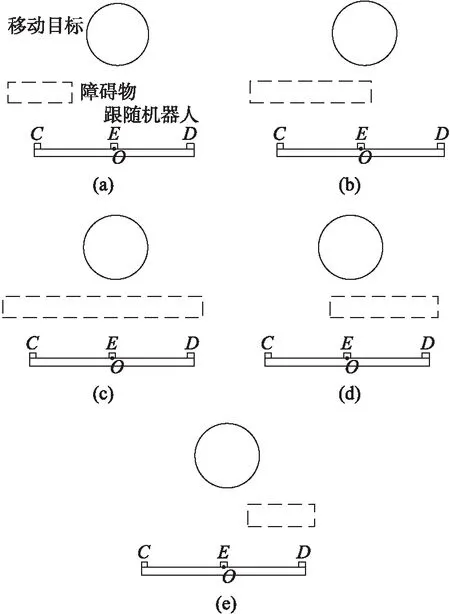
图5 遇障方式

当障碍物状态如图5(a)所示时,测距模块C将测出自主跟随机器人到障碍物的距离,D、E不能测到障碍物,此时自主跟随机器人可以判断出左侧有障碍物,并根据障碍物的距离,控制向右转向的角度和速度,图5(e)状态与此相似;当障碍物状态如图5(b)所示时,测距模块C、E将测出自主跟随机器人到障碍物的距离,D不能测到障碍物,此时自主跟随机器人可以判断出左侧和中间有障碍物,并根据障碍物的距离,控制向右转向的角度和速度,图5(d)状态与此相似;当障碍物状态如图5(c)所示时,测距模块C、D、E将测出自主跟随机器人到障碍物的距离,此时自主跟随机器人只能通过提示告知移动目标已丢失跟踪目标。

4 多信号源定位及避障实验

根据某工程的应用需求,需要在500 mm～2500 mm范围内实现自主跟随,跟随精度要求为±30 mm。本次实验在移动目标上的以100 mm为半径的圆上均匀安装12个超声波传感器(JSN-SR04T分体式超声波传感器,其最远射程可达4 m,精度为5 mm,发射角度60°),并将超声波传感器顺时针从1开始编号,其中1号超声波传感器正对前进方向。在自主跟随跟随机器人上的两个信号接收节点距离为400 mm,超声波测距模块(HC-SR04一体式超声波传感器,其最远射程可达4 m,精度为5 mm)以200 mm间隔排布,整个装置的示意图如图2所示。本文使用无线模块(NRF24L01)作为通信模块和同步超声波信号的发射与接收。

为了测试本文方法的定位精度和定位效果,本文设计了一个自主跟随定位实验。将自主跟随机器人固定不动,使移动目标在距离两信号接受节点所连成的直线50 0 mm、1 000 mm、1 500 mm、2 000 mm、2 500 mm的平行直线上移动,起点和终点在垂直方向上距离O点1 000 mm,如图6所示。

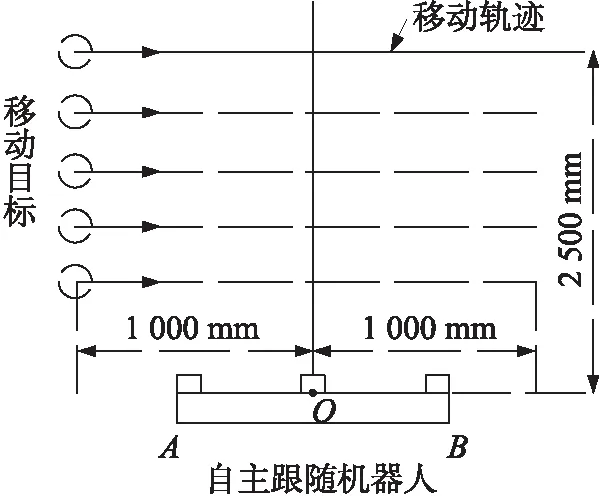
图6 定位实验示意图

从起点开始,每隔100 mm记录一个数据,将测量结果用MATLAB绘制成图,其轨迹结果如图7所示。所记录的数据x坐标误差、y坐标误差如图8所示。移动姿态方向偏差如图9所示。

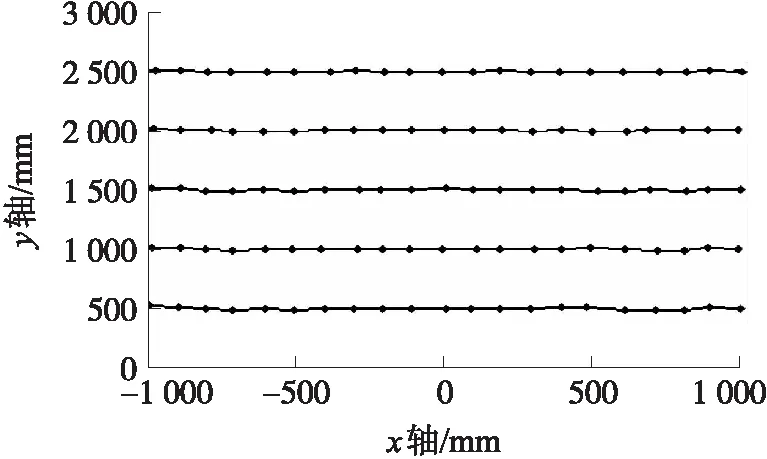
图7 测量轨迹

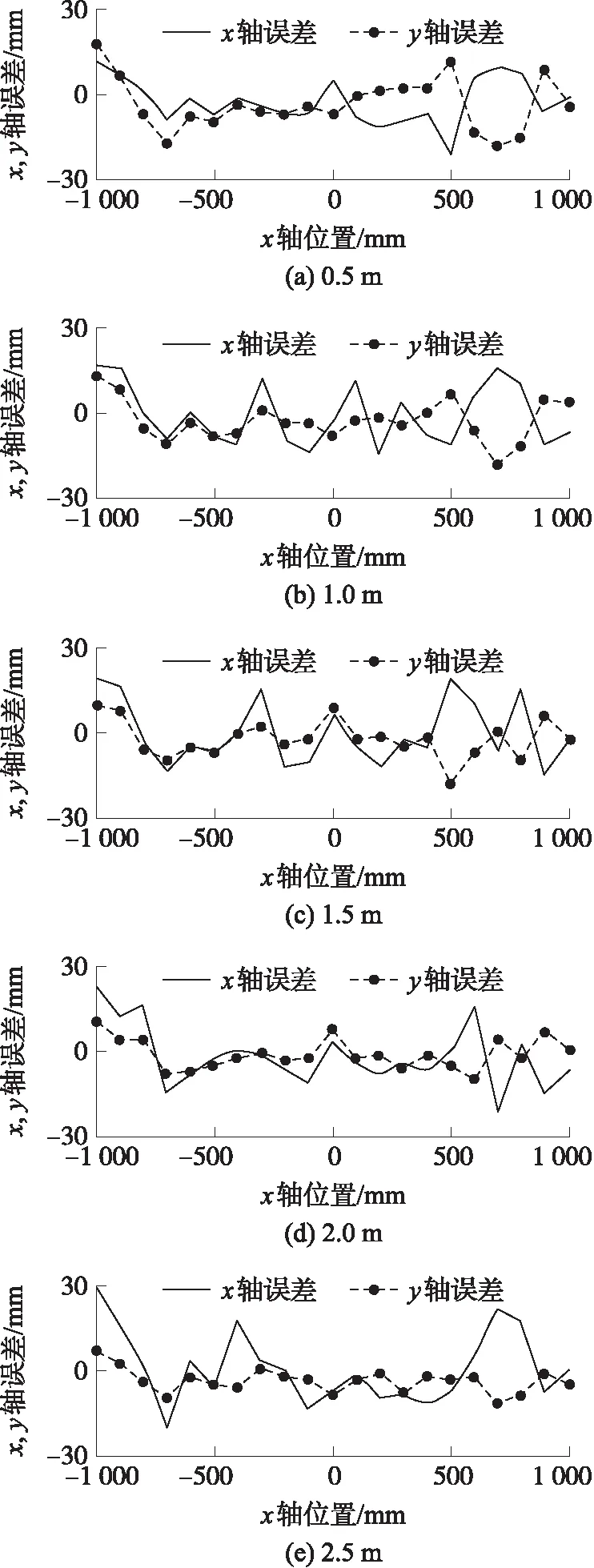
图8 x、y坐标误差曲线

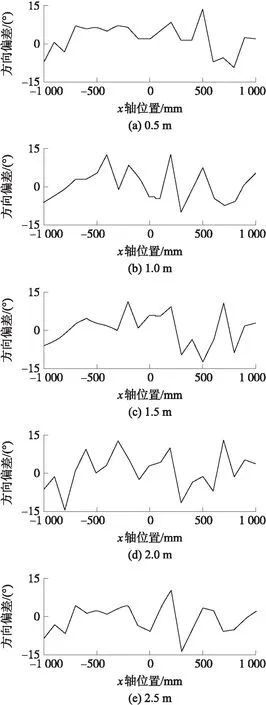
图9 移动姿态方向偏差

由图7可知,自主跟随机器人测量移动目标的轨迹与实际轨迹偏差很小,由图8、图9可知,x轴误差和y轴误差在±30 mm以内,方向偏角在±15°以内,能够满足跟随的精度要求。

为了验证本方法的避障能力,使自主跟随机器人随移动目标前进,并在其跟随过程中添加如图5所示障碍,实验结果显示,障碍在图5(a)、5(b)、5(d)、5(e)状态下,自主跟随机器人能避开障碍物,及时跟随移动目标前进,在图5(c)状态下,自主跟随机器人丢失跟随目标。

5 结论

本文提出了一种基于多传感器信息融合的自主跟随定位及避障方法,该方法通过增加多信号源,使自主跟随机器人与移动目标之间建立冗余信道,弥补了单一信号源发射角度小的问题;通过多传感器信息融合,能够准确的计算出移动目标的位置和实时移动姿态;合理的使用测距模块,能够有效的避开多种情况下的障碍。本文建立了多信号源模型和算法,对该算法进行了实验,实验结果表明,该算法能够准确的对移动目标进行定位和移动姿态测量,并且能够避开障碍,保持跟随,具有一定的工程应用价值。