基于Fick-小波包变换方法对土壤CO2浓度时间序列的去噪处理*
谢宝良,胡军国,李烨斐,陈 芳,毛国平
(浙江农林大学信息工程学院,林业感知技术与智能装备国家林业和草原局重点实验室,浙江省林业智能监测与信息技术研究重点实验室,杭州 311300)
土壤有机碳库是陆地碳库的重要组成部分,总储量达到1 394 PgC,因此其库容的微小变化都会对大气CO2浓度及全球气候产生巨大影响[1]。然而,土壤呼吸的动力学仍在不断探究中,导致全球碳通量分析受到很大限制[2-3]。因此针对土壤呼吸的精确测定也成为研究生态系统碳循环和地球温暖化的关键问题之一[4]。
土壤CO2浓度扩散包括两个主要过程:土壤中二氧化碳的产生及其在土壤中的传输,并通过土壤表面碳从土壤扩散到大气的这个过程[5],主要方法涉及以下两大类,一类是微气象学法[6],另一类是气室测定法[7]。微气象法主要利用涡度相关法,但是易受到较低风速脉动的影响[8],不能准确测定土壤呼吸。气室法是在土壤表面安装用金属或树脂制作的气室,根据气室内从土壤表面向大气扩散CO2的速率进而算出土壤呼吸速率的方法[9]。这种测定方法的优点是能观测到小范围的土壤呼吸特性及其细微的变化。但在受到空间不均一性的影响下,进行大尺度扩展同样有一定的困难。目前针对气室法精确测定土壤呼吸的仪器有美国LI-COR公司的LI-8100开路式土壤碳通量测量系统[10],但是价格昂贵,并且随着测量室对气体长时间的监测获取会影响土壤CO2的扩散,影响土壤呼吸的监测值。Bekku Y等[11]发现气室内的环境与外界环境会产生一定差异,对测定土壤呼吸产生一定的噪声。而一般的开放型土壤呼吸监测仪在计算土壤呼吸时易受到气压、温度、传感器质量、浓度梯度、扩散系数、算法等综合因素的干扰,导致监测获取的土壤CO2时间序列噪声过大,而一般的去噪方法无法很好的对非线性土壤CO2时间序列进行去噪分析,导致最终计算得到的土壤呼吸值与LI-8100开路式土壤碳通量测量系统测得的值相差太大,非常不精确,无法用来研究土壤呼吸。因此,若要精确测得土壤呼吸,必须要对收集得到的土壤CO2浓度进行去噪分析。王国英等[12]利用自主研制的设备监测获取了土壤CO2并对其进行小波变换去噪分析,从而获得较高质量的碳通量数据,最后再结合合适的算法实现了对土壤呼吸的动态监测。
本文研制了一种开放型的土壤呼吸监测仪,如图一所示,主要由三个传感器分层组合而成,并结合扩散原理设计了一种新的算法,用来获取高质量的土壤CO2数据。首先利用Fick第二定律计算分析出浓度梯度在垂直方向扩散的滞后时间,并以此对时间序列进行时移,然后运用小波包变换对土壤CO2浓度进行分析去噪,得到的结果利用距离度量[13]来评价CO2浓度时间序列与实际时间序列的相似性。接下来利用Fick第一定律求出碳通量值与LI-8100开路式土壤碳通量测量系统测得的碳通量值进行对比,综合得出了以下几个结论:①利用数据计算分析发现了CO2在垂直方向上的扩散规律与Fick扩散定律吻合;②Fick定律与小波包变换结合处理得到了气室内任意时刻任意位置的高质量CO2数据,并利用处理后的数据计算得到了与 LI-8100 相近的碳通量值;③通过本文算法及研制的设备可以在未来替代LI-8100,从而节约大量研究成本。
1 方法介绍
1.1 数据来源
土壤呼吸排放的CO2会由高浓度向低浓度扩散,考虑到气体扩散的规律,采用描述物质扩散的Fick定律作为建模的理论基础。该模型设计的测量仪器为一个开放式测量仪,如图1所示。将测量仪器放置在土壤表面,土壤呼吸产生的气体首先聚集在仪器底部,当仪器底部的浓度比上部的浓度高时,气体发生扩散,最后扩散出仪器,扩散过程如图1中红色箭头所示。仪器内部传感器每隔一段时间采集一次数据,然后将采集的数据发送到服务器端,最后利用Fick定律建模并计算出土壤碳通量。
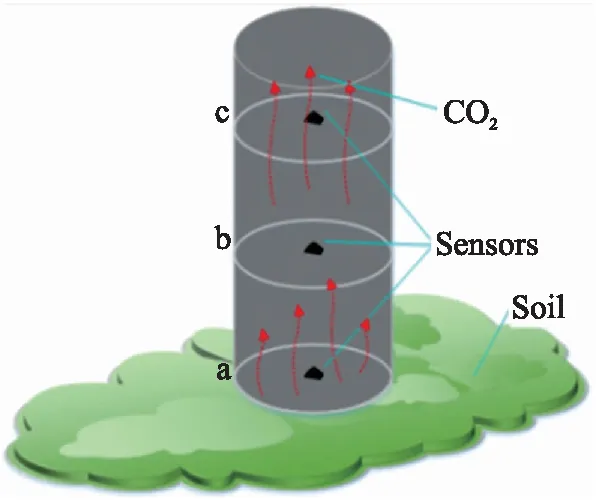
图1 土壤呼吸监测仪
1.2 Fick定理
Fick定律是描述物质扩散现象的宏观规律,这是生物学家Fick于1855年发现的。Fick定律包括第一定律和第二定律。Fick定律在各个行业发挥着重要作用[14-16]。第一定律描述的是在单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量),用J表示与该截面处的浓度梯度成正比,即
(1)
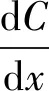
Fick第二定律描述的是在非稳态扩散过程中,在距离x处浓度随时间的变化率等于该处的扩散通量随距离变化率的负值,即
(2)
式中:C为扩散物质的浓度,t为扩散时间,x扩散的距离,D为扩散系数,如式(3)所示。
(3)
式中:T为热力学温度,P为大气压强,μA、μB为气体的分子量,本文研究CO2气体在空气中扩散,因此μA=44,μB=29。VA、VB为气体A、B在正常沸点时液态克摩尔容积,VA=34,VB=29.9。从式(3)可以知道扩散系数D只与测量环境的温度和大气压强有关,跟扩散气体的浓度无关。测量仪器可以实时测量当前环境的温度和大气压强,实时更新扩散系数D。
本文研究的气体扩散问题属于非稳态扩散,因此利用Fick第二定律对土壤呼吸排放的二氧化碳进行计算。得到如下方程:
(4)
式中:C为CO2浓度;t为CO2在监测仪内的扩散时间;x为CO2在监测仪内的扩散距离;D为CO2在监测仪内的扩散系数;C0为扩散到监测仪顶部的CO2;Cs为土壤扩散到监测仪内的CO2。
解得:
(5)
式中:erf(·)为误差函数,
(6)
1.3 小波包变换
由于本装置传感器精度较低,在实验过程中易受外界环境影响,测得的CO2浓度值存在着较大的噪声。因此通过小波包变换对非线性时间序列进行分析去噪,来获取更高质量的CO2浓度时间序列,提高土壤呼吸监测仪的监测精度。
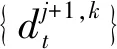
(7)
式中:S为信号;A为低频;D为高频。
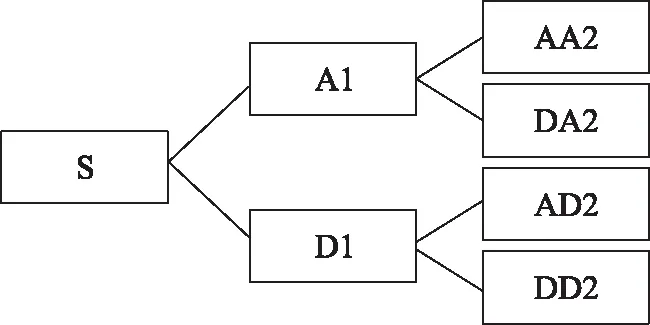
图2 小波包分解示意图
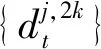
(8)
式中:h,g为滤波器系数;d为小波包分解系数;p,t为分解层数;j,k为小波包节点号。
1.4 评价指标
利用第2节中的2017年10月份采集的浙江省杭州市临安区武肃街666号的6个传感器采样间隔为10 s的二氧化碳数据,进行小波包变换处理。为了说明小波包变换在土壤二氧化碳去噪分析上的优越性,利用下列公式来说明方法的优越性:
①斜率距离
首先对时间序列进行分段线性化,主要由重要点来确定分段。本文将极值点作为重要点对时间序列进行分段线性化,步骤如下:
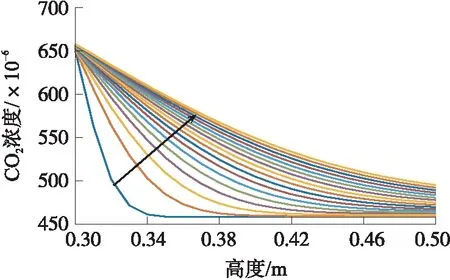
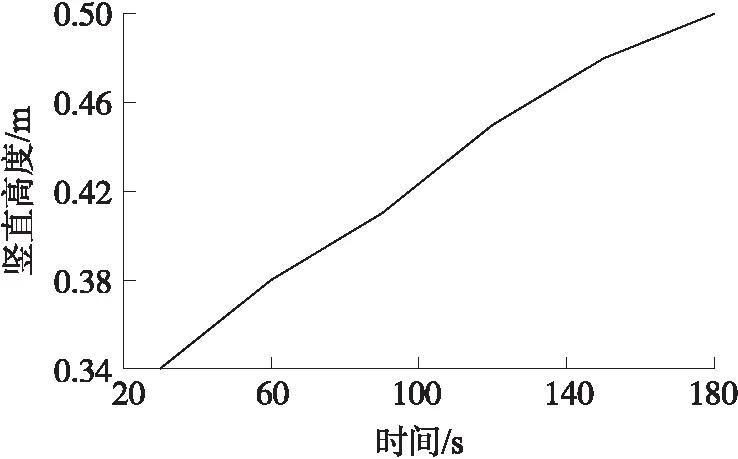
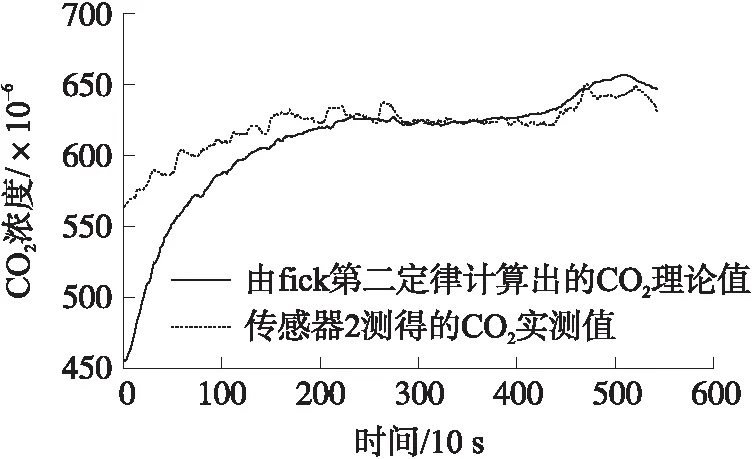
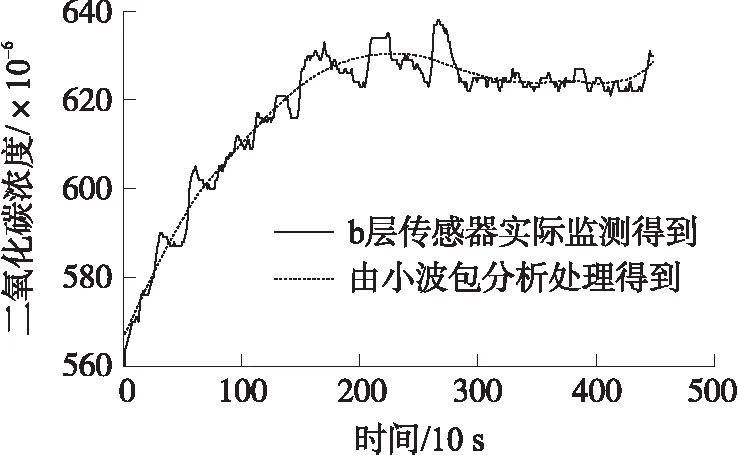
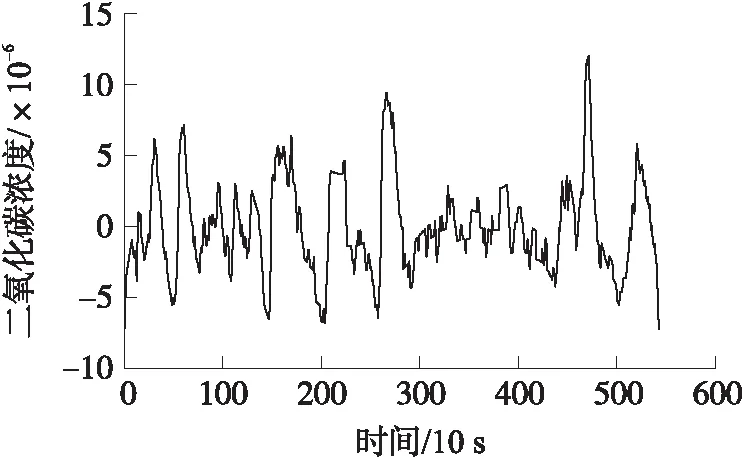
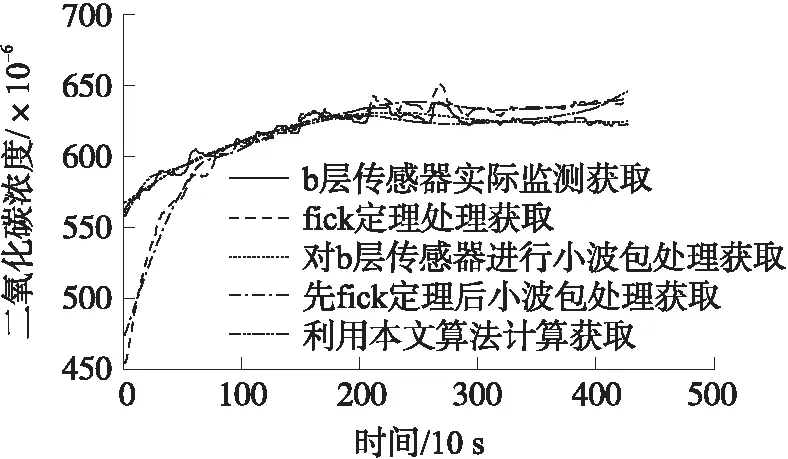
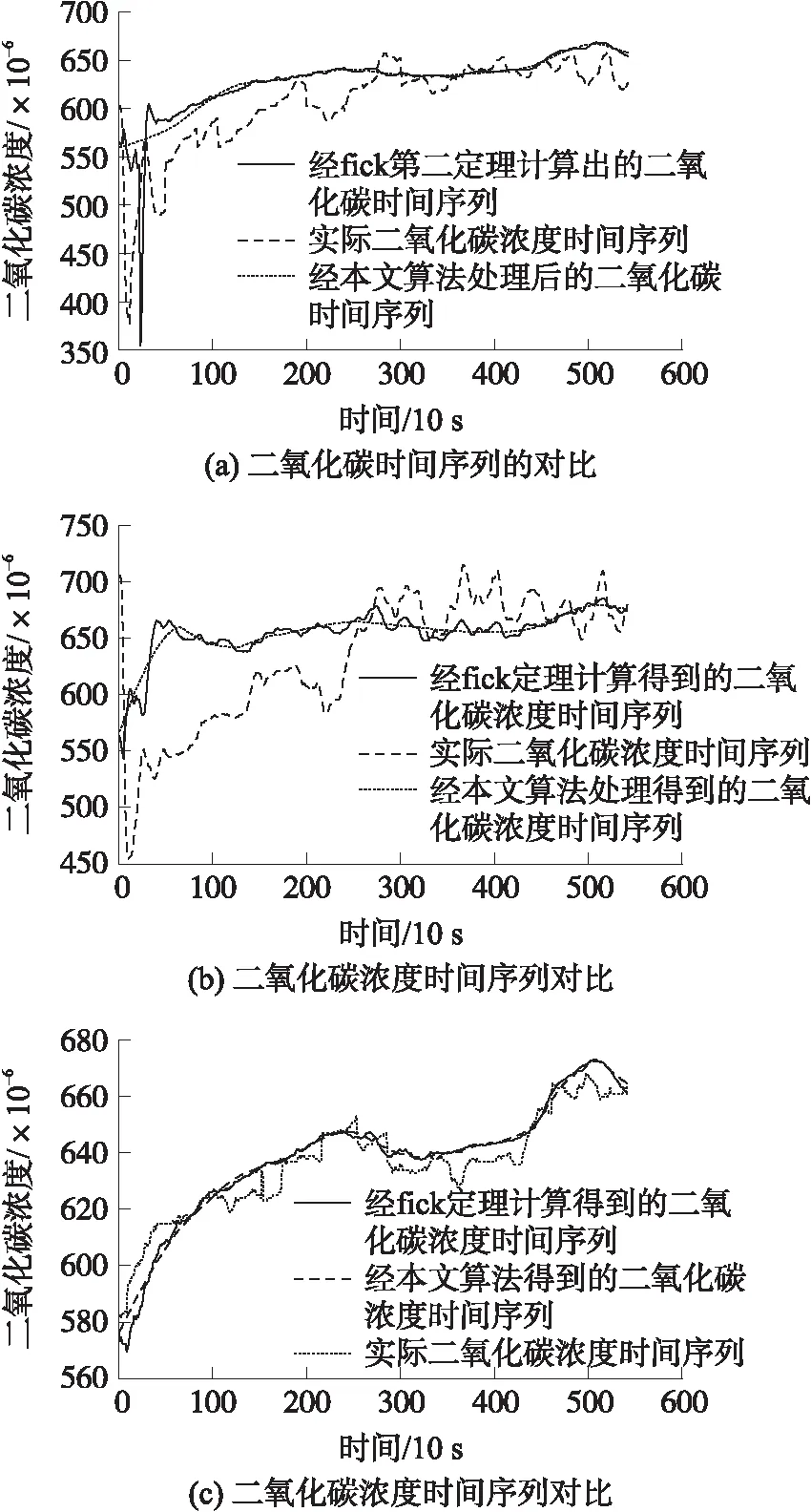
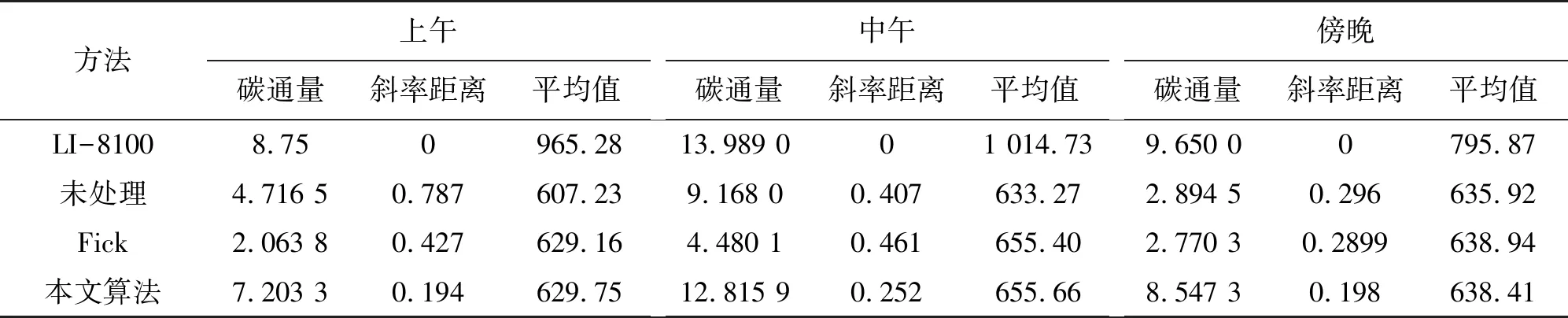
若给定时间序列X=(x1,x2,…,xn),参数R>1,若xm∈X(1 上述步骤给出了xm是重要极大值点满足的条件:xm为子序列X[i:j]中的最大值点,且xm与子序列两个端点的比值大于参数R。通过参数R可以控制时间序列分段的精细度,R值越大选中重要点越少,分段越粗,反之分段就越细。类似的,重要极小值点定义如下: 若给定时间序列X=(x1,x2,…,xn),参数R>1,若xm∈X(1 对于获得的极值点,我们将其进行按顺序排列,得到X=(x1,s1,s2,…,sk,xn),对极值点间进行线性拟合,得到如下一元线性分段函数模型: (9) 式中:bi为直线的斜率估计值,i=1,2,…,k,代表分段趋势大小;ai为直线的截距估计值,i=1,2,…,k;ei(t)为零均值白噪声,i=1,2,…,k,表示一段时间内时间序列与它的分段线性表示之间的误差。 通过以上步骤,可以获得如下公式: S=([b1,s1-x1],[b2,s2-s1],…,[bk,sk-sk-1], (10) 这里我们将公式稍作修改方便后面的计算,令: (11) 则可得: S=([b1,l1],[b2,l2],…,[bk,lk],[bn,ln]) (12) 接下来,利用上述公式计算斜率距离来分析时间序列A和时间序列B的相似性。在本文中,斜率距离越小,代表两时间序列越接近。公式如下: (13) ②信噪比SNR(Signal-to-Noise Ratio),公式定义为: (14) ③原始信号与降噪信号之间的均方根误差RMSE(Root Mean Squared Error),定义如下: (15) 在利用Fick定律计算由开放型气室法测得的土壤CO2值时,存在着以下几个问题:①由开放型气室测得的土壤CO2时间序列含噪声过大,会影响后续的Fick定律计算得到的碳通量值;②气室中各个高度的CO2值不相同,并且随着土壤CO2扩散,各层传感器在何时接收到CO2也不相同,导致无法辨识时间序列的去噪时间段。针对上述两个问题,本文利用小波包变换在处理时间序列噪声的优势上,结合Fick第二定律能计算出CO2随着时间和空间的扩散,提高了开放型气室法测得的CO2浓度值的质量。 步骤1首先将图一中的a层和c层传感器测得的CO2浓度时间序列μ(a,t)和ψ(c,t)代入式(5)中,得到: (16) 令式中x=b,则可得到b层传感器的理论CO2浓度时间序列,即 (17) 步骤2通过Fick第二定律计算出CO2浓度在竖直高度上的扩散变化,通过连接转折处,分析得到CO2浓度在竖直高度上随时间变化的关系图,拟合得到CO2浓度在竖直高度上随时间变化的关系式,即 x=kt+b (18) 式中:x为高度,t为时间。 利用式(18)作为门限标准选取需要去噪的时间段,即 x(t)=x(T)-x(t′) (19) 式中:T∈[0,N],t′∈[0,(x-b)/k]。 步骤3将新获得的时间序列作为去噪对象,对每一高度处的CO2浓度时间序列C(x,t)进行小波包变换。步骤如下:①时间序列的小波包分解。选择一个小波并确定一个小波分解的层次N,然后对时间序列C(x,t)进行N层小波包分解。②计算最佳树(即确定最佳小波包基)。对于一个给定的熵标准来计算最佳树。③小波包分解系数的阈值量化。对每一个小波包分解系数,选择一个适当的阈值并对系数进行阈值量化。④小波包重构。根据第N层的小波包分解系数和经过量化处理系数,进行小波包重构。 步骤4通过重构后的时间序列计算气室内的浓度梯度,并将其代入Fick第一定律里,计算得到土壤碳通量。 数据选取2017年12月份同一研究区域的CO2浓度时间序列,将a层传感器和c层传感器测得的CO2浓度值代到Fick第二定律中,求得随着时间变化,CO2浓度从a传感器扩散到c传感器的变化规律,如图3所示。 图3 随时间变化的CO2浓度在竖直高度上的扩散变化图 图4 二氧化碳浓度随时间在竖直高度上的变化关系图 从图3可得,由Fick第二定律计算出的CO2在垂直高度扩散时,需要一定的时间。而浓度梯度则随着时间的增加不断的变小。这里,我们将图三曲线各个转折处的点坐标重新描绘到一个平面坐标系中,如图4所示,可以得到CO2浓度随时间在竖直高度上的关系式为x=0.001t+0.31,说明CO2在开放型监测仪内是较为均匀扩散的,扩散10 cm所需要的时间大约为90 s左右。在实验中,由于土壤呼吸监测仪放置在土壤上方后不是立即测量,存在着一定的系统误差。并且测量仪内本身含有CO2,导致3个传感器在同时测量时已经发生扩散,与理论值发生一定的偏差,如图五所示。因此,本文将由Fick第二定律计算分析得到的CO2浓度随时间在竖直高度上的变化关系作为门限进行时移来确定去噪时间段。 图5 二氧化碳的理论值与实测值之间的对比 为了更好的说明本文算法的优越性,实验选取了同一天内不同时间段以及不同环境下的CO2浓度时间序列进行测试。首先为了验证仪器的可行性,将LI-8100仪器横放置于封闭室内地面,同时将本实验装置土壤呼吸监测仪也横放置于封闭室内地面进行监测。LI-8100仪器显示CO2浓度均值477.4×10-6,碳通量值为-0.03 μmol/(m2/s),土壤呼吸监测仪的三个传感器的CO2浓度均值分别为505.77×10-6,501.26×10-6,500.41×10-6,利用Fick定理计算出来的碳通量值为0.01 μmol/(m2/s)。可以发现,虽然通过本实验装置计算得到的碳通量值相近,但可能具有一定的偶然性,而且传感器测得的数据质量并不是很理想,因此为了克服这一问题,选择合适的算法,可以使本装置应用于土壤呼吸的监测,具有非常大的意义。本文选取了2017年12月份的一组实验的数据,利用MATLAB软件及其中的wavemenu进行处理。根据第三节所述算法,这里我们的小波包变换最终选取的最佳小波包基为sym5,并且对时间序列进行6层分解,阈值选取的是threshold,数值为2。首先,我们对b层传感器测得的CO2浓度时间序列进行小波包分析,得到如图6所示,并且得到了如图7所示的剩余误差。接下来我们以处理之后的b层数据作为标准与其他方法计算得到的数据进行对比。然后,我们将a层传感器和c层传感器进行分析计算,分别利用Fick定理、Fick定理算出之后由小波包分析直接处理和Fick定理与小波包分析结合的方法算出的b层传感器的CO2浓度时间序列与标准进行对比。从图8和表1可以看到,无论从图像、RMSE、信噪比和时间序列相似性上看,本文算法都比其他方法优秀。从图8看,利用本文算法得到的时间序列非常平滑,与标准时间序列及实际监测得到的时间序列都非常接近。而利用其他方法得到的时间序列,虽然在700 s左右之后与实际时间序列和标准时间序列接近,但是在0~700 s左右与实际和标准时间序列相差甚远。说明,若没有利用Fick第二定律分析得到的时差,会导致前期的时间序列与实际不符。从表1可以看出,本文算法得到时序信噪比为8.340 4,接近标准时序信噪比14.351 1,而其他方法得到的时序则出现了负值,明显噪声过大,数据质量不利于后续的土壤呼吸研究;RMSE上,本文算法仅为6.279 9与标准时序3.143 5接近,而其他算法计算得到的RMSE超过了20,与标准相差过大;时序相似性上,本文算法与先小波后Fick计算得到的时间序列与标准相比分别为0.217 4和0.221 6,而Fick计算得到的为0.440 9,与标准相似度过低。综上,利用本文算法,可以更好的结合Fick第二定律,精确算出气室内各个位置各个时间点的CO2浓度值。 表1 验证结果 图6 二氧化碳浓度时间序列对比 图7 处理之后得到的剩余误差 图8 算法比较 为了探究算法得到的数据是否具有更加实际的意义,本文分别在2018年8月9号的上午9点到10点半,中午12点到1点半,下午6点到7点半三个时间段对研究区域进行了土壤呼吸监测的对比实验。本次实验为了提高数据的质量,分别将3个传感器放置于开放型监测仪内的0.1 m,0.2 m,0.3 m处进行监测土壤CO2浓度时间序列,每一个传感器看作一个气室,之间的距离为1 cm。首先通过本文算法,计算出0.2 cm处的理论值,并和实际值及用Fick定理算出来的理论值进行对比,如图9所示。 图9 早中晚二氧化碳浓度时间序列对比 从图9可以看到,图9(a)(上午)和图9(c)(傍晚)的计算结果非常优秀,图9(b)(中午)的计算结果相对较差,可能是因为温度影响了最终计算结果。但总体来说最终结果还是非常出色的,说明通过本文算法,可以非常精确的计算出气室内各个位置,各个时间段的CO2浓度值。因此,本文利用算法进一步计算出土壤的碳通量值,并与其他的评价指标来分析算法更广泛的实际意义,如表2所示。 从表中可以看到,首先,经过本文算法处理得到的碳通量值明显与LI-8100测得的碳通量值非常接近,并且比未处理及Fick定理计算得到的更加优秀;其次,针对CO2浓度时间序列,经本文算法处理之后的时间序列与LI-8100监测得到的时间序列更为相似,而未处理的时间序列及Fick定理计算得到的理论时间序列与LI-8100相比,相似度过低,从图9中也可以发现,这两组时间序列起伏波动非常大,稳定性过低;最后从平均值角度来看,未处理的时间序列,用Fick定理及本文算法处理的时间序列的浓度平均值都比LI-8100监测得到的浓度平均值低,但相比较而言,用Fick定理及本文算法处理得到的浓度平均值略优于未处理的浓度平均值。综上所述,经过本文算法处理,不仅能够精确的算出各个时间点各个气室位置的CO2浓度值,而且算出来的碳通量值也与LI-8100测得的非常接近。因此,利用本文算法,能够非常好的克服传感器的质量问题以及开放型气室所存在的隐含问题,同时所测得的土壤呼吸值又具有非常重要的实际意义,利用较廉价的实验设备获取了非常高的实验结果,对土壤呼吸测量具有非常大的意义。 表2 验证结果 其中碳通量值的单位为μmol/(m2/s),平均值单位为10-6。 Coifman和Wickerhauser于20世纪90年代初提出了小波包WP(Wavelet Packet)分析,不仅对低通子带进行分解,而且也对高通分量分解,从而聚焦到感兴趣的任意频段,突破了小波分析对信号频带进行等Q划分的局限性。因此,利用小波包变换可以有效的对非平稳时间序列进行去噪分析,实现一般去噪方法无法得到的效果,并且已经在各领域取得了一定的成就[17-21]。而小波包变换结合其他方法能够更加合理的解决非线性时间序列数据中产生的问题,这种方法已经应用到土壤学领域,取得了比单独一种方法更加精确有效的结果[22-23]。 Fick扩散定律由阿道夫·菲克于1855年提出,能够在不依靠宏观的混合作用发生的传质现象时,描述分子扩散过程中传质通量与浓度梯度之间关系的定律。基于Fick定律的预测模型,并利用其他针对性的方法对数据进行处理的方式,能够取得比单一Fick定律更加精确有效的结论[24-25]。 本文结合上述两种方法的优点,首先基于Fick定律能描述非稳态扩散过程中土壤CO2浓度时间序列的变化,计算分析出需要去噪的时间段。接下来利用小波包对时间序列的高频信号和低频信号逐层分解,利用软阈值对数据进行去噪,最后重构得到质量较高的时间序列。通过分析比较时间序列以及通过时间序列计算得到的土壤碳通量值,进一步证明了该方法的有效性和可靠性。但是在小波包基的选取上和气室间的距离,还需要进一步探究。 本文通过结合小波包变换和Fick定理将其运用到计算土壤CO2浓度时间序列,获得了比单独使用小波包变换和Fick定理更加精确的时间序列。同时利用本文算法求得的时间序列,运用到Fick第一定律中,计算得到的了与LI-8100测得的相近的土壤碳量值。通过廉价的实验设备和适当的算法,获得了与费用昂贵的土壤呼吸监测仪相近的土壤呼吸值,具有非常重要的意义。但是,本文自制的实验设备在野外测量仍会受到较大的环境因素影响,因此改进实验设备使其具有在野外更好的适应能力在以后的研究中可以进一步考虑。
[bn,xn-sk])2 Fick-WPT方法介绍
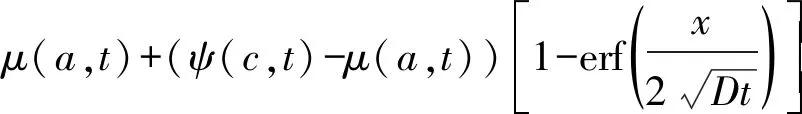
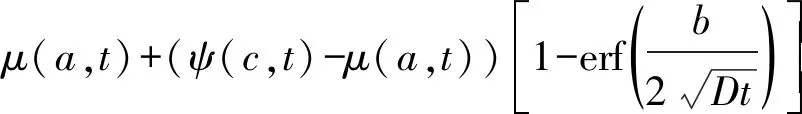
3 实验结果与分析
3.1 Fick第二定律对CO2浓度时间序列的分析
3.2 Fick-WPT方法与其他方法之间的对比

3.3 Fick-WPT方法在不同时间段计算得到的碳通量值与传统LI-8100对比
4 讨论
5 结论

