基于犹豫梯形模糊Bonferroni Mean算子的多属性决策*

黄咏婷，成央金，杨 柳

(湘潭大学数学与计算科学学院，湖南 湘潭 411105 )

Zadeh[1]在1965年提出了隶属度函数的概念，建立了模糊集理论.该理论在现代社会的各个领域应用广泛，众多学者展开了深入研究.Atanassov[2]提出了非隶属度和犹豫度的概念，建立了直觉模糊集理论；Vicen[3]针对人们在进行决策时总是犹豫不决，而又为了保证信息的全面性最终产生一个集合的隶属度的情况，提出了犹豫模糊集的概念；于倩等[4]针对专家在决策过程中由于问题的复杂性和模糊性，对方案的评价值难以用定量的数值形式来表示的情况，基于犹豫模糊集和梯形模糊数，提出了犹豫梯形模糊集的概念.

1950年，Bonferroni[5]提出了Bonferroni均值.由于Bonferroni均值能够很好地捕获输入变量之间相互关联的情况，将多个输入变量集成为1个变量，因此学者们对其进行了拓展研究.Yager[6]提出了广义Bonferroni mean算子并将其应用到多属性决策中；结合直觉模糊集和区间直觉模糊集，徐泽水等提出了直觉模糊Bonferroni mean算子[7]和区间直觉模糊Bonferroni mean算子[8]，并将它们用于多属性决策中；结合三角模糊数直觉模糊集、梯形模糊数直觉模糊集和区间直觉梯形模糊集，周晓辉等提出了三角模糊数直觉模糊Bonferroni mean算子[9]、梯形模糊数直觉模糊Bonferroni mean算子[10]和区间直觉梯形模糊Bonferroni mean算子[11]，并将它们用于多属性决策中；朱斌等[12]结合犹豫模糊集提出了犹豫模糊几何Bonferroni mean算子；朱轮等[13]提出了广义犹豫模糊Bonferroni mean算子；于倩等[14]结合区间犹豫模糊集提出了区间犹豫Bonferroni mean算子；夏梅梅等[15]提出了几何Bonferroni mean算子并将其用于多属性决策中.笔者拟考虑专家评价值为犹豫梯形模糊元的多属性决策问题，结合Bonferroni均值和犹豫梯形模糊集，提出犹豫梯形模糊Bonferroni mean算子的概念,并研究其加权形式.

1 预备知识

1.1 Bonferroni均值

定义1[5]设p,q>0,ai(i=1,2,…,n)是一列非负实数，若存在

则称函数Bp,q为Bonferroni均值.

1.2 犹豫梯形模糊集

定义2[4]设X为一非空集合，则定义在集合上的犹豫梯形模糊数集可表示为A={x,hA(x)|x∈X}，其中hA(x)由[0,1]范围内所有不同梯形模糊数构成，表示元素x(∈X)隶属于集合A的所有不同隶属度的集合.为了方便，用hA(x)表示一个犹豫梯形模糊元素(HTrFE)，记为hA(x)=h={[a,b,c,d]}.

定义3[4]设h={[a,b,c,d]},h1={[a1,b1,c1,d1]}，h2={[a2,b2,c2,d2]}，它们都是犹豫梯形模糊元素，且λ>0，则有如下运算规则：(1)h1⊕h2=∪[ai,bi,ci,di]∈hi,i=1,2{[a1+a2-a1a2,b1+b2-b1b2,c1+c2-c1c2,d1+d2-d1d2]}；(2)h1⊗h2=∪[ai,bi,ci,di]∈hi,i=1,2{[a1a2,b1b2,c1c2,d1d2]}；(3)hλ=∪[a,b,c,d]∈h{[aλ,bλ,cλ,dλ]}；(4)λh=∪[a,b,c,d]∈h{[1-(1-a)λ,1-(1-b)λ,1-(1-c)λ,1-(1-d)λ]}.

对于犹豫梯形模糊元素h1和h2，若s(h1)>s(h2)，则h1>h2；若s(h1)=s(h2)，则h1=h2.对于h1和h2的大小，也可以用这个方法进行比较.

2 犹豫梯形模糊Bonferroni Mean算子

2.1 犹豫梯形模糊元的运算律

定理1设h1，h2，h3是犹豫梯形模糊元，则它们满足如下运算律：(1)h1⊕h2=h2⊕h1；(2)h1⊗h2=h2⊗h1；(3)(h1⊕h2)⊕h3=h1⊕(h2⊕h3)；(4)(h1⊗h2)⊗h3=h1⊗(h2⊗h3)；(5)(h1⊗h2)λ=h1λ⊗h2λ；(6)λ(h1⊕h2)=λh1⊕λh2.

证明由定义3易证运算律(1)，(2)，(4)，(5).现证运算律(3)：

(h1⊕h2)⊕h3={[a1+a2-a1a2,b1+b2-b1b2,c1+c2-c1c2,d1+d2-d1d2]|

[ai,bi,ci,di]∈hi,i=1,2}⊕h={[a1+a2+a3-a1a2-a1a3-a1a2a3+

a2a3,b1+b2+b3-b1b2-b1b3-b1b2b3+b2b3,c1+c2+c3-

c1c2-c1c3-c2c3+c1c2c3,d1+d2+d3-d1d2-d1d3-

d2d3+d1d2d3]|[ai,bi,ci,di]∈hi,i=1,2,3}=

{[1-(1-a1)(1-(a2+a3-a2a3)),1-(1-b1)(1-(b2+b3-b2b3)),

1-(1-c1)(1-(c2+c3-c2c3)),1-(1-d1)(1-(d2+d3-d2d3))]|

[ai,bi,ci,di]∈hi,i=1,2,3}=h1⊕(h2⊕h3).

再证运算律(6)：

λ(h1⊕h2)={[1-(1-(a1+a2-a1a2))λ,1-(1-(b1+b2-b1b2))λ,1-(1-(c1+c2-c1c2))λ,

1-(1-(d1+d2-d1d2))λ]|[ai,bi,ci,di]∈hi,i=1,2}=

{[1-(1-a1)λ(1-a2)λ,1-(1-b1)λ(1-b2)λ,1-(1-c1)λ(1-c2)λ

1-(1-d1)λ(1-d2)λ]|[ai,bi,ci,di]∈hi,i=1,2}=λh1⊕λh2.

2.2 犹豫梯形模糊Bonferroni Mean算子

定义5令p,q>0,hi(i=1,2,…,n)是一列犹豫梯形模糊元，若

则称HTrFBMp,q是犹豫梯形模糊Bonferroni mean算子.

定理2设p,q>0,hi(i=1,2,…,n)是一列犹豫梯形模糊元，则用HTrFBMp,q算子集成的结果仍是犹豫梯形模糊元，且

证明由定理1可知，

故只要证明下式成立即可：

(1)

现利用数学归纳法证明.当n=2时，

(2)

此时(1)式成立.假设当n=k时(1)式也成立，则

当n=k+1时，

再用数学归纳法证明

(3)

当k=2时，由(2)式可知，

此时(3)式成立.假设当k=t时(3)式也成立，则

(4)

当k=t+1时，由(2)和(4)式可知，

故(3)式成立.于是

故(1)式成立，从而

再由定义3的(3)和(4)可得，

由HTrFBMp,q算子的以上形式和定义2易知HTrFBMp,q算子的集成结果仍是犹豫梯形模糊元.

HTrFBMp,q算子还具有如下性质：

定理3(幂等性) 设p=q=1,hi(i=1,2,…,n)是一列犹豫梯形模糊元，且对于∀i∈{1,2,…,n}都有hi=h={[a,b,c,d]}，则

HTrFBMp,q(h1,h2,…,hn)=HTrFBMp,q(h,h,…,h)=h.

定理4(置换不变性) 设p,q>0,hi(i=1,2,…,n)是一列犹豫梯形模糊元，hσ(i)(i=1,2,…,n)是该列犹豫模糊元的任意一个置换，则

HTrFBMp,q(hσ(1),hσ(2),…,hσ(n))=HTrFBMp,q(h1,h2,…,hn).

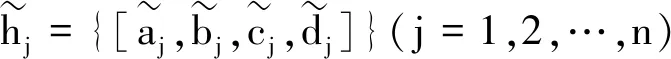
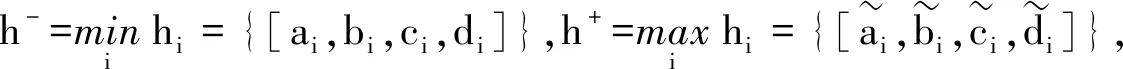
h-≤HTrFBMp,q(h1,h2,…,hn)≤h+.

2.3 犹豫梯形模糊加权Bonferroni Mean算子

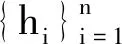
则称WHTrFBMp,q为犹豫梯形模糊加权Bonferroni mean算子.

定理7的证明过程与定理2类似，不再详述.

3 HTrFBMp,q算子的特例

(1)若q→0,则

(2)若p=1,q→0，则

(3)若p=q=1，则

4 基于WHTrFBMp,q算子的多属性决策方法

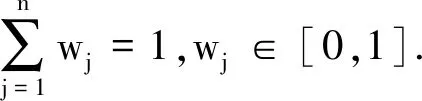
下面基于WHTrFBMp,q算子给出解决犹豫梯形模糊环境下的多属性决策问题的具体步骤：

(ⅰ)利用犹豫梯形模糊矩阵和WHTrFBMp,q算子，计算得到方案Ai的综合犹豫梯形模糊评价值

其中：

(5)

5 数值实例

例1[4]假设5个绿色供应商(Ai，i=1,2,3,4,5)分别从4个属性(Cj，j=1,2,3,4)去评价，其中C1为产品竞争力，C2为合作与发展潜力，C3为供应商竞争力，C4为绿色绩效.w是这4个属性的权重向量，w=(0.2,0.4,0.1,0.3)T.专家给出的各备选绿色供应商在上述4个属性下的评价值用犹豫梯形模糊元表示，汇集所有的评价值，构成犹豫梯形模糊决策矩阵H=(hij)5×4(表1).

现用WHTrFBMp,q算子来解决犹豫梯形模糊环境下的绿色供应商选择问题：

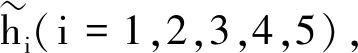
由此可知，最优供应商是A1,这与文献[4]的结论相同，验证了该算子的有效性.

表2 犹豫梯形模糊综合评价值Table 2 Hesitant Trapezoid Fuzzy Comprehensive Evaluation Value

表3 犹豫梯形模糊综合评价值的得分函数Table 3 Hesitant Trapezoid Fuzzy Comprehensive Evaluation Score Functions

6 结语

将Bonferroni mean算子与犹豫梯形模糊集相结合，给出了犹豫梯形模糊Bonferroni mean算子及其加权形式的定义和具体的计算公式，并研究了犹豫梯形模糊Bonferroni mean算子的一些性质及其特殊形式，给出了基于犹豫梯形模糊加权Bonferroni mean算子的多属性决策方法.实例结果表明，犹豫梯形模糊加权Bonferroni mean算子在决策应用中是有效的，但对于在犹豫梯形模糊环境下的各属性权重未知的多属性决策或群决策问题，还有待进一步研究.