金属冶炼碳含量控制中的内模控制
潘昊天, 尤 文
(长春工业大学 电气与电子工程学院, 吉林 长春 130012)
0 引 言
氩氧精炼铁合金过程是一个复杂的高温过程,由于各种化学反应和不可测扰动的影响,加上其很大的滞后性、时变性,采用常规的控制方法很难控制碳的含量,且精度不高。对此,提出一种内模控制算法,并将其应用在金属冶炼碳含量控制系统中,与传统的PID控制进行仿真结果比较,验证所提方法的控制效果。
1 估计模型的建立
1.1 模型假设
由于铁水中的碳氧反应处于1 600 ℃以上的高温,反应物[C]和[O]的扩散速率一般要低于界面化学反应速率,所以反应物的扩散是碳氧反应的限制环节。
1.2 过程速率方程
[O]传质过程是碳氧反应限制环节。氧的传质速率为
(1)
式中:JO----氧的扩散速率,mol·s-1;
A----CO气泡表面积,m2;
βO----氧在铁水中的传质系数,m·s-1;
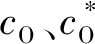
同时,由于碳氧反应速率等同于铁水中氧的减少速率。碳氧反应速率JR为
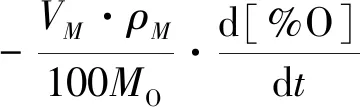
(2)
式中:JR----碳氧反应速率,mol·s-1;
nO----氧的物质的量,mol;
t----反应时间,s;
VM----铁水体积,m3;
ρM----铁水密度,g·m-3;
MO----氧的摩尔质量,g·mol-1。
在稳态条件下,式(1)和式(2)相等,即
(3)
式(3)中各参数确定如下:
1)βO的确定。氧在铁水中的传质系数βO可由表面更新理论确定,因为
(4)
式中:De----氧的有效扩散系数,m2·s-1;
u----气泡上浮速度,m·s-1;
d----气泡直径,m。
上述参数由水模拟实验研究结果所得。
2)cO的确定。根据浓度换算:
(5)

(6)
以下确定[O]*,对于碳氧反应
[C]+[O]=CO
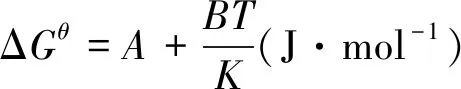
(7)
平衡常数:
(8)
因为氧的传质为限制性环节,所以在反应界面处的氧浓度[%O]*与碳氧反应平衡时的氧浓度[%O]e相等,即
[%O]e=[%O]*
(9)
另外,同样是因为氧的传质是限制性环节,所以碳浓度存在下列关系:
[%C]e=[%C]*=[%C]内
(10)
式中:[%C]内----铁水内部碳的浓度。
将式(9)和式(10)代入式(8),得
(11)
将式(11)代入式(6),得
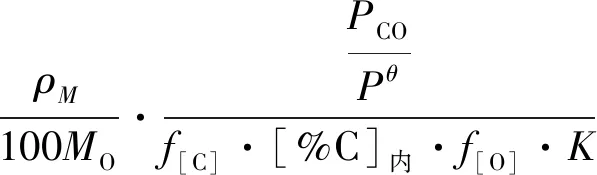
(12)
再将式(3)~式(5)代入式(12),得
(13)
则式(13)可改写为
(14)
积分式(14)
(15)
整理得t时刻铁水中的碳氧关系式为
[%O]={[%O]0-b}exp(-at)+b
(16)
将确定的模型参数代入式(16)并进行拉普拉斯变换,有:
(17)
2 内模控制及控制器设计
2.1 内模控制器

(18)
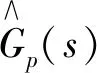
(19)
其中
(20)
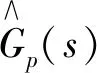
(21)
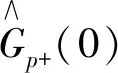
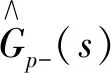
Tf----滤波器时间常数。
考虑了滤波器以后的实际推理控制器为
(22)
2.2 内模控制特点
内模控制结构框图如图1所示。
图1 内模控制系统结构框图
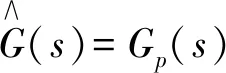
Y(s)=D(s)[1-GIMC(s)Gp]=
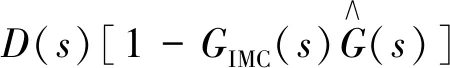
(23)
假设“模型可倒”,即
(24)
将式(24)代入式(23)得
Y(s)=0
(25)
式(25)表明,不管D(s)如何变化,对Y(s)的影响为零,说明设计的控制器是克服扰动的理想控制器。
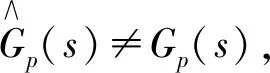
(26)
在阶跃不可测扰动作用下,系统输出的稳态偏差为
Y(0)=0
(27)
式(26)和式(27)表明,不管模型有什么误差,系统输出总是稳态无偏。
3 内模控制和PID控制的仿真
3.1 模型参数选取
Tf值的选取不能太大也不能太小,太大影响系统响应速度,太小又不能兼顾系统的鲁棒性。最终选取Tf=40时内模控制的碳含量控制系统。
3.2 内模控制与PID控制效果比较
当控制对象不变,系统无扰动输入且输入阶跃信号,利用Matlab的Simulink仿真平台搭建系统仿真框图,将内模控制与PID控制结果进行比较,输出波形如图2所示。
实线----内模控制输出响应曲线; 虚线----PID控制输出响应曲线
内模控制响应速度优于PID控制,很快进入稳定状态。
4 结 语
在氩氧精炼铁合金过程中,建立估计模型并运用内模控制方法可有效解决扰动不可测的控制问题,通过与PID控制进行仿真对比得出结果,内模控制在含有不可测扰动的碳含量控制对象上,响应速度与鲁棒性都优于PID控制。

