万有引力形成机制与暗物质谬误研究

钱凤仪

(吉林大学 研究生院， 吉林 长春 130012)

0 引 言

1932年，美国加州工学院的瑞士天文学家弗里兹·扎维奇最早提出证据并推断暗物质的存在。弗里兹·扎维奇观测螺旋星系旋转速度时，发现星系外侧的旋转速度比牛顿重力预期的快，故推测必有数量庞大的质能拉住星系外侧组成，以使其不致因过大的离心力而脱离星系。这个庞大的质能就是后来科学家命名出来的暗物质。宇宙不是专门为牛顿定律和爱因斯坦相对论所设计的。如果现有的物理理论不足以描素宇宙的蓝图时，我们的出路不是让宇宙中的事实符合现有的理论，而是让理论符合宇宙法则。事实上，暗物质的提出，正是我们认为现有的理论是毫无疑问的正确性所导致的。文中通过揭示万有引力形成的原因，揭示出牛顿所提出的“万有引力常数”是和引力源成正比的“变数”。这就说明我们通过天文观测到猜想可能存在的暗物质，是以牛顿“万有引力常数”是个不变量为依据所导致的错误结果。如果推导出牛顿万有引力公式，并证明所谓的“万有引力常数”并不是常数，自然就能消除我们主观上臆断的所谓暗物质现象。

1 形成万有引力机制的理论依据

根据广义相对论史瓦希德解，如果恒星塌陷成黑洞，则星球的“黑洞”几何半径为[1]

(1)

式中:G----牛顿万有引力常数;

M----引力源质量;

c----光速。

根据狭义相对论，此时星球的固有能量也就是其与所处空间交换的能量为

E(r)=Mc2

(2)

E(r)的微分形式为[2]：

dE(r)=f(r)M4πr2dr

(3)

因为星体需要与空间交换能量，因此导致星体外部空间形成能量梯度，进而形成引力场。因此，物体或星体在其外部空间形成的引力场是星体或物体与空间交换能量时所形成的缺欠能量空间。换而言之，当某一空间区域有物体或星体存在时，会使得这一空间区域的能量分布发生变化，而且空间距离与物体或星体越近，这一空间区域的能量就相对越缺少。而缺欠能量的总量为式(2)所示的爱因斯坦在狭义相对论中所得出的量值(固有能量)。

由式(2)和式(3)可知，星体形成的引力场在空间形成的缺欠能量，积分形式为：

(4)

如果f(r)最一般形式是关于r4的反比关系，则式(4)是收敛的。因为E(M)=Mc2是个有限量，故可令

(5)

式中：kb----常数。

由式(4)通过积分可知

(6)

由式(4)可知，从r处至r→∞处空间因为引力源的存在而导致的缺欠能量值为

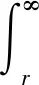
(7)

即

(8)

若将一个质量为m的物体等效地分布在以引力源为中心、以r为半径的球面上，则由于引力场导致空间能量的分布不均匀，而对物体m施加有不对称的交换能量，这就是万有引力的成因。

将式(8)写成微分形式，则有

(9)

一个质量为m的物体所具有的势能微分形式为

(10)

式中：km----物体能将空间势能转化为物体获得的引力势能的比例常数。

由功能转化定律可知

Fm(r)dr=dEm(r)

(11)

由式(9)和式(11)可知，物体在另一个物体所形成的缺欠能量空间中所受到的作用力为

(12)

式(12)就是牛顿万有引力定律的一般表达形式,而且，定律只考虑到了较大质量的M所导致的万有引力，忽略了较小质量的m所导致的万有引力。式(1)～式(12)的理论推导过程表明，物体或星体与空间交换能量时，在空间形成了能量梯度，进而形成了引力场。

2 牛顿万有引力定律的引力常数问题

由爱因斯坦光量子方程可知，光子在惯性或平坦空间的能量表达式为[3]：

Ep(r)=Mpc2

(13)

式中：mp----光子的质量。

由广义相对论可知，光子在引力场中沿径向传播时的速度表达式为

(14)

由式(13)和式(14)可知，光子从距离∞→r处时，光子的速度变化量为：

(15)

光子在引力场中传播时，其速度的减小而转化为其频率的增加，而速度减小部分导致的能量缺失，反映的是空间缺欠能量的变化程度。

光子从r→∞传播到r处光子的能量变化量ΔEp(r)为：

ΔEp(r)=mpc2-mp[c(r)]2=

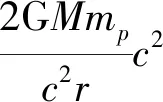
(16)

式中：mp----光子质量。

光子从rb→∞的能量变化值为：

ΔE(rb)=mpc2

(17)

由光子的能量变化量推知在地球表面以外，空间向星体提供的能量所占比例为

(18)

所以

(19)

在地球表面r=rse处，空间缺欠能量所占比例为

(20)

已知地球质量Me、地球中心到表面的距离rse、引力常数光速值分别为

Me=5.96×1024kg

rse=6.37×106m

G=6.67×10-11N·m2/kg2

c=3.00×108m/s

将以上数值代入式(20)可得

ΔE(rs→∞)=1.39×10-9(Mec2)

(21)

式(21)表明，地球表面以外向地球提供的“固有能量”仅仅是地球“固有能量”的极小部分。

已知太阳质量Ms、地球中心到表面的距离rss：

Ms=1.99×1030kg

rs=6.96×108m

将以上数值代入式(20)可得

ΔE(rs→∞)=4.2×10-6(Msc2)

(22)

式(22)表明，太阳表面以外向太阳提供的“固有能量”仅仅是太阳“固有能量”的极小部分。

这就说明了为什么万有引力的强度远远小于电磁力和核力强度的原因。

由式(1)、式(6)、式(12)可得万有引力公式的一般表达形式为

(23)

反之，m对M产生的万有引力为

(24)

由式(23)和式(24)可知，两个星体之间的万有引力一般形式为

(25)

3 万有引力常数与暗物质问题的谬误

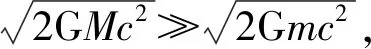
4 结 语

事实上，爱因斯坦通过广义相对论修正了由牛顿万有引力定律给出水星近日点的进动问题，也修正了相应的光线弯曲问题[1]。文中借助相对论解决万有引力常数问题，能从理论上解释清楚为什么会遇到“暗物质”的问题。而且按太阳系内的万有引力常数来计算其他星系星体运动问题，会发现星系内有巨大的“暗物质”在发挥引力作用。