改进FCM的MR脑肿瘤图像分割

蒋秋霖， 王 昕

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

胶质瘤主要由胶质母细胞病变和周围组织浸润形成[1]，是成人中最常见的脑瘤，占恶性肿瘤的80%以上[2]。在外科治疗计划中，胶质瘤的分割是一项非常重要且具有挑战性的任务[3]，是后续评估胶质瘤的基础。 因此胶质瘤是肿瘤分割的重点对象。

模糊C均值(FCM)是一种常用的模糊聚类算法，已广泛应用于图像处理等领域[4]。FCM算法是基于最小化目标函数寻找最优的聚类中心，但FCM算法初始聚类中心的随机选择将导致算法的不稳定聚类。每个聚类结果都不同，聚类精度也很低[5]。国内外学者对此研究了众多改进算法。Chang等[6]把稀疏正则化引入到 FCM 的目标函数中，使聚类的准确率提高。Elazab等[7]结合具有相邻空间信息的自适应正则化项改进FCM，使得FCM算法的鲁棒性提高，同时提升了图像分割的精确度。Wang Yan等[8]将正则化项引入FCM的目标函数中，使得聚类的精度和稳定性显著提高。Cai W等[9]提出的快速广义模糊C均值分割算法(FGFCM 算法)，其中加入了局部区域像素间灰度关系和空间关系。先利用像素之间相似性生成一张和图像，再对和图像的直方图进行聚类，提升了图像的分割效果和效率。Ma等[10]在FGFCM算法的基础上提出了一种结合非局部空间信息的模糊聚类算法，该算法使用像素间结构相似性来定义空间约束项，然后将基于此得到的和图像引入 FGFCM 算法框架中求解，使分割结果更加精确。

文中提出了一种结合优化粒子群算法的改进模糊C均值聚类算法来分割脑肿瘤图像。模糊C均值聚类算法广泛应用于聚类中心，未确定聚类中心将导致分割结果不理想。特别是在类似类别的情况下，相同图像的分割很可能在分割结果中存在很大差异。为了解决这个缺陷，首先通过优化粒子群算法得到聚类中心，然后结合空间信息来改进FCM。这不仅保持了模糊C均值聚类算法的稳定性，而且提高了算法的分割精度。

1 算法描述

当FCM算法用于分割脑肿瘤图像时，初始聚类中心对结果的影响极大。初始中心点的不同经常会导致聚类结果的差异，并且所得到的聚类结果非常不稳定。粒子群优化算法(PSO)具有强大的全局搜索能力，但其收敛速度在后期减慢，并且可能存在过早的现象。针对这些问题，文中提出了一种结合优化PSO的改进FCM聚类算法，该算法结合正弦函数和余弦函数动态调整粒子的惯性权重系数。提高PSO的全局搜索性能，加速粒子群的后期收敛，避免粒子群进入局部极值，并利用粒子群搜索全局最优初始簇中心。抑制了FCM算法对初始聚类中心选择的灵敏度，并且在FCM中考虑了图像的空间信息，获得理想的脑肿瘤分割结果。

1.1 改进的粒子群算法

1.1.1 粒子群算法

PSO是Kennedy等[10]提出的一种新型群体智能算法，用于模拟鸟类觅食过程中的群体行为。 它是解决聚类NP难题最广泛使用的方法之一。众多学者在聚类分析中加入PSO。例如，文献[11]为解决传统数据流聚类问题，在滑动窗口模型的数据流聚类中加入PSO将其改进。在PSO中，粒子基于他们自己的经验(个人的最佳位置)和团队共享的社会经验(该组的最佳位置)在全局最优解的方向上改变其速度和位置。通过当前位置的预定义适应度函数来评估粒子的性能。假设种群规模为m的粒子群在n维空间搜索时，如果粒子的个体最佳位置是Pbest，这个种群的最佳位置是Gbest，可以根据以下公式调整每个粒子的飞行速度Vi=(vi1,vi2,…,vin)及其位置Xi=(xi1,xi2,…,xin)(i=1,2,…,n):

Vi(t+1)=wVi(t)+c1r1(Pbesti-Xi)+c2r2(Gbesti-Xi)

(1)

Xi(t+1)=Xi(t)+Vi(t+1)

(2)

式中：t----迭代次数的变量；

w----惯性权重系数；

c1、c2----学习因子，常数；

r1、r2----均匀分布在[0,1]范围内的随机数。

1.1.2 正余弦算法

正余弦算法(Sine Cosine Algorithm, SCA)因其不是模拟自然界中的某些生物现象而产生的，因此不需要假设条件。更新SCA算法的解的过程是通过随机数与转换概率的比较来决定其是进行余弦操作还是正弦操作，公式更新如下：

(3)

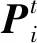
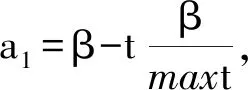
a2----取值为[0,2π]之间的一个随机数，决定的是移动距离；

a3----随机权重，取值为[0,2]之间的一个随机数，a3>1表示对下一次迭代影响效果明显，而a3<1则表示不明显；

a4----取值为[0,1]之间的一个随机数。

SCA算法中的两个重要参数分别是搜索的方向a2和距离a3。

1.1.3 改进的粒子群算法

正弦函数和余弦函数的值属于[-1,1]区间内，因此SCA优化过程可以看成正弦波或余弦波传播的过程，而波传播过程中能量会逐渐减小，正弦波或余弦波最后必定固定在某个值上，由此得出SCA是收敛的，所以SCA可以加强粒子群算法的收敛性能。因此，将SCA算法加入粒子群会获得更好的最优结果。

将式(1)代入式(2)：

Xi(t+1)=Xi(t)+wVi(t)+c1r1(Pbesti-Xi)+c2r2(Gbesti-Xi)

(4)

将式(4)结合正余弦算法：

(5)

在粒子群优化算法中，惯性权重w值越大，算法的全局搜索能力越强。理想的粒子群算法是早期的全局搜索能力较强，后期的局部搜索能力较强，因此文中粒子群算法的w值可采用以下线性调整策略:

(6)

式中：tmax----粒子群的最大迭代次数；

wmax----最大惯性权重；

wmin----最小惯性权重，一般取0。

风险管理是单位或个人用来降低消极结果的一种决策过程,通过风险识别评估和风险评价的手段来降低可能出现的风险[1]。由于外科护理管理过程中,患者会因为各种因素出现安全事故,因此护理人员在遵医嘱进行护理操作时还应该加强风险意识,规避可能存在的潜在风险,促进患者恢复。

文中提出的是一种递减机制的权重，当t→0时，w=wmax；当t→tmax时，w=wmin，可以满足算法搜索的前期所需要的寻优空间；之后，它可以收敛到最佳值并加速收敛。 由于w和a1均为递减函数，且在t→0时取最大，t→tmax时最小且为0，故设wmax=β，则

(7)

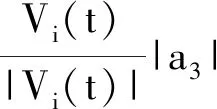
(8)

1.2 改进的FCM聚类算法

1.2.1 FCM聚类算法

FCM算法是一种模糊聚类。权重矩阵不再是0～1矩阵，而是计算对应于整个样本的每个聚类中心的隶属矩阵。核心收敛原理是采用经典的误差平方和准则，即目标函数为

(9)

式中：k----聚类数目；

N----样本元素总和；

xj----样本中第j个元素；

ci----第i个聚类中心；

d(xj,ci)=‖xj-ci‖2

(10)

式(9)中ωij为xj对应ci的隶属度，m为权重指数，ωji应满足

(11)

隶属度矩阵尺寸为N×k，其中各个元素由下式得出

(12)

在获得隶属中心矩阵之后，通过样本元素与下式组合来修改聚类中心ci。

(13)

由式(12)、式(13)反复迭代修正，直至目标函数J最小。通常，算法的收敛条件为两次迭代的聚类中心之间差值小于阈值，‖ci+1-ci‖<ε，或者达到指定的迭代次数。

1.2.2 改进的FCM算法

在脑肿瘤图像分割中，某个点的像素值不是孤立的，并且在与周边相邻的像素值之间存在连接。然而，传统的FCM算法没有考虑到它，即不考虑图像的空间信息。 当脑肿瘤图像受到噪声或边缘不清晰的影响时，传统的FCM算法会使图像分割不充分，导致像素点的分类不正确，得不到满意的分割结果。

综合上述缺点，文中考虑将惩罚项加入传统FCM算法的目标函数中，以表示邻域像素值的影响。带惩罚项的目标函数为

(14)

式中：∂----惩罚项系数；

ξ----惩罚项。

在图像分割过程中，惩罚项的存在可以有效地约束空间信息，从而提高像素聚类的准确性。特别是当图像受到噪声或不清晰边缘的影响时，惩罚项将发挥更重要的作用。

惩罚项ξ说明的是空间信息，因此考虑引入局部区域间的像素关系和空间位置关系。在脑肿瘤图像中，样本中的第j个元素和第i个聚类中心之间的相似性sij为

(15)

式中：ai----图像中第i个聚类中心像素的灰度值；

bj----第j个元素的灰度值；

(pi,qi)----ai的坐标；

(pj,qj)----bj的坐标；

λs、λg----分别为控制距离差异的度量因子和灰度差异影响相似性度量值的尺度因子，λs和λg值越大，对相似程度的影响越小，λs通常取值是3，λg取值在[0.5,6][9]；

σi----局部区域的平坦度，其公式为

(16)

式中：Ni----第i个聚类中心局部区域内像素点的集合；

K----Ni集合中不包括中心像素点的个数。

改进后的FCM算法目标函数为

(17)

为了求解式(17)中的惩罚项参数α，对式(17)的优化问题构造拉格朗日函数：

(18)

式中：λi----拉格朗日因子，待定参数；

ωij、ci----待定参数。

将这些参数一阶偏导数设为零，求解其最优值。首先对式(18)中ωij求偏导数

(19)

由式(19)推导出ωij的迭代更新表达式为

(20)

其次，将式(18)对λi求偏导数

(21)

将式(21)代入式(19)可得λi的更新表达式

(22)

最后，参数ci求偏导数由式(18)给出

(23)

从式(23)获取聚类中心ci的更新迭代表达式

(24)

式(20)的ωij与式(24)的隶属度ci有关，而ci与惩罚项参数α有关。因此，为了提高FCM聚类算法的稳定性和聚类精度，可以使用PSO算法优化惩罚项参数α。

1.3 算法实现步骤

文中提出的基于改进PSO算法的FCM聚类算法描述如下:

输入：MR脑肿瘤图像，聚类数目k，粒子群的种群规模m以及最大迭代次数tmax。

输出：聚类中心不再更改的分割结果。

算法步骤如下：

1)进行初始化操作。初始化迭代次数t=0；初始化粒子速度Vi、个体最优位置Pbesti、群体最优位置Gbesti。

2)设定聚类数目k。从给定的脑肿瘤图像中随机选择n个中心点作为粒子位置Xi的初值。

3)执行粒子群迭代搜索的PSO算法。根据式(1)和式(8)分别更新粒子的速度和位置。最终得到X(t+1)为初始聚类中心c0。

4)设置权重指数为m，迭代停止阈值ε>0，初始聚类中心c0。

5)根据式(20)更新隶属度矩阵；根据式(24)更新聚类中心。

6)若|ci+1-ci|<ε，则算法停止；否则重复4)、5)，并置i=i+1。

2 实验结果及分析

为了验证算法的性能，文中对当地三甲医院的核磁共振脑肿瘤图像进行了分割实验。比较分析了该算法得到的区域生长算法、水平集算法、FCM算法的实验结果。 实验平台为Windos7操作系统，酷睿i5 6300HQ处理器，8 GB内存，Matlab 2015b[12]。文中列出了三种MR肿瘤图像的分割结果，分别如图1～图3所示。

(a) 原始图像 (b) 水平集模型 (c) 区域生长算法

(d) FCM算法 (e) 文中算法 (f) 专家分割

(a) 原始图像 (b) 水平集模型 (c) 区域生长算法

(d) FCM算法 (e) 文中算法 (f) 专家分割

(a) 原始图像 (b) 水平集模型 (c) 区域生长算法

(d) FCM算法 (e) 文中算法 (f) 专家分割

图1中的脑肿瘤区域更为明显。 但是对于水肿和浸润区域的分割不太理想。 图2和图3的脑肿瘤区域变得愈加不清晰，边界变得更加模糊，水平集模型还是能大致分割出脑肿瘤区域，但是在边界处的分割上存在误差；区域生长算法和FCM算法在分割时对肿瘤区域的阴影部分的分割存在误差(见图1(c)、图2(c)和图3(c))。分割结果出现孔洞，又因其没有考虑图像空间像素之间的关系,导致分割边界时判断边界点是否是目标点出现误差，从而无法获得最佳分割结果。该算法提出在考虑像素空间关系的同时优化初始聚类中心，保证了每个分割结果的稳定性。

为了更客观地评估分割结果，精确度(真阳性、TP、肿瘤的正确分割)和假阳性率(假阳性、FP、正常组织错误分类为肿瘤部位)和漏检率(假阴性、FN、未分割的肿瘤部分)对每种算法的分割结果进行平均后再进行定量分析，结果见表1。

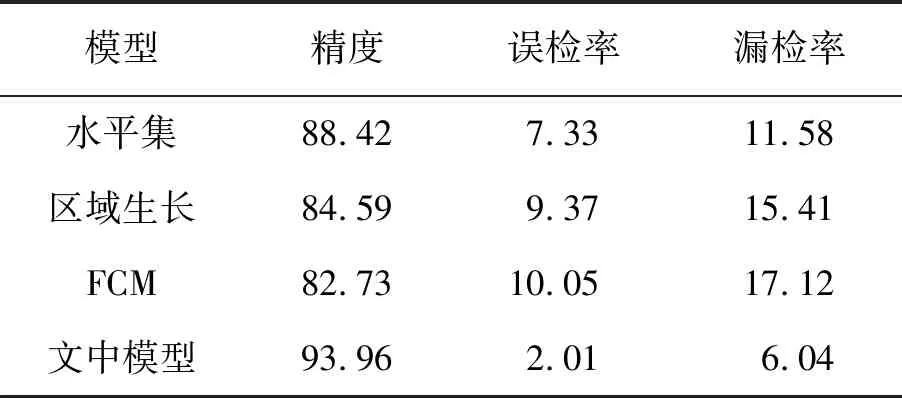
表1 不同算法的分割结果 %

文中模型比其他两种算法更准确，误检率和漏检率更低。

3 结 语

提出了一种改进的粒子群优化算法，该算法将改进的模糊C均值聚类算法与脑肿瘤图像分割相结合。首先用优化的粒子群算法求得初始聚类中心，再将初始聚类中心代入添加了空间信息惩罚项的FCM进行计算，最后实现脑肿瘤准确分割。文中所提算法利用优化矩阵和空间邻域像素值克服了FCM因聚类中心选择而影响分割结果，并且MR脑肿瘤边界不清楚，引起分割误差的问题。