液压机械无级变速器的变论域模糊PID速比跟踪控制
于 今 陈 华 刘骏豪
1.重庆大学机械传动国家重点实验室,重庆,400044 2.重庆大学机械工程学院,重庆,400044
0 引言
液压机械无级变速器(hydro-mechanical continuously variable transmission,HMCVT)是一种复合型无级变速器,由机械路与液压路组成,其中机械路主要用于传递大功率和扩大传动范围,液压路主要用于实现无级调速与传递小功率[1-3]。HMCVT综合了液压传动无级变速和机械传动效率高的两方面特点,已经应用在部分特种车辆上[2,4-6]。同金属带式无级变速器控制类似,HMCVT通过对目标速比的跟踪控制,间接控制发动机的转速,使发动机工作在最佳工作点,因此具备一个稳定、有效的速比跟踪控制策略显得尤为重要[1,6-8]。
国内外部分高校和研究单位对HMCVT的速比控制策略进行了相关研究。韩国成均馆大学进行了发动机-液压机械传动最优控制曲线研究[9]。文献[1]提出了离散控制系统,文献[6,8,10]的研究集中在模糊PID的控制。由于模糊控制不依赖于完整的精确数学模型,所以模糊控制在HMCVT这类复杂的系统中应用较为广泛[1,7,8,10],但是由于复合变速器的速比跟踪控制较为复杂,常规模糊PID控制仍然存在速比跟踪控制效果不佳、适应性不强和动态品质不佳等问题[10-11]。为解决以上问题,本文设计了基于量化因子和决策因子的变论域模糊PID控制器并搭建了AMESim和Simulink联合仿真平台。
1 液压机械无级变速器数学模型
1.1 基本传动结构
本文所研究的HMCVT传动结构简图见图1。该系统由1个行星排、1个变排量液压元件和1个定排量液压元件构成,当系统工作时,由a1轴输入的功率经过行星排A分流,一路经过齿轮传动到由变量泵-定量马达构成的容积调速液压回路,一路经过齿轮进入机械传动部分,最后两路功率经过a2轴汇流并输出到负载。图1中箭头的方向表明了HMCVT在不发生功率循环下的功率流向。通过调节变量泵的排量,进而调节了液压路的传动比,实现整个HMCVT的速比的改变。

图1 液压机械无级变速器基本结构Fig.1 The basic structure of HMCVT
1.2 变速器基本模型
1.2.1轴系模型
根据动力学的基本建模方法,可以得到各轴传递的扭矩和转速。
T?1=z?1T?13T?2=z?2T?52
ω?3=z?1ω?4
(1)
ω?5=z?2ω?2
(2)
ω?1+Aω?3-1+A?ω?2=0
(3)
A?=-k?/(1+k?)
其中,ai?为第i?轴的表示符号;T?i?为第i?轴的输入扭矩;T?ij?为i?轴齿轮到j?轴齿轮传递的扭矩;ω?i?为第i?轴的转速;J?i?为i? 轴的转动惯量;B?i?为i? 轴的黏性阻尼;z?1为a3轴与a4轴的传动比;z?2为a2轴与a5轴的传动比;T?p为变量泵的输入扭矩;T?m为马达的输出扭矩;T?为负载力矩。k?为行星排特性参数,其取值范围为2.5~4[3]。联立式(1)~式(3)可得变速器静态速比i?H表达式:
i?H=m?/[1+A?m?-Az?1z?2]
其中,m?为变量泵与定量马达的排量比。
1.2.2变量泵-定量马达模型
针对本文采用的变量泵-定量马达系统,可以得到定量马达输出转速ω?m关于泵斜盘摆角θ?(等效为排量比m?)和输出扭矩T?m的传递函数:
其中,ω?n为液压部分固有频率;ξ?n为阻尼比;ω?p为泵的输入转速;D?m为液压泵的排量;ω?m为马达的输出转速;θ?为变量泵变量机构的摆角,在本文中将摆角等效为排量比;k?p为排量梯度;β?e为油液的有效体积的弹性模量;J?t为液压马达及负载的转动惯量之和;V?0为泵和马达的工作容积;C?t为泵和马达总泄漏系数;B?m为黏性阻尼。
2 变论域模糊PID控制器的设计
2.1 变论域模糊PID控制系统总体设计
变论域模糊PID控制是在常规模糊PID控制的基础上,加入变论域模糊控制的思想,解决一般模糊PID在控制过程中存在的缺点和不足[11-12]。HMCVT变论域模糊PID控制框图见图2。这里采用一种基于量化因子(K?e?和K?ec?)和决策因子(K?u?)收缩的方法来对模糊论域进行伸缩。其中PID参数模糊控制器就是根据模糊规则表来设计的,控制系统的关键是要得到优化的K?P、K?I和K?D。首先找到一组相对较优的初始值,量化因子模糊控制器和决策因子模糊控制器通过系统偏差e?和偏差变化率ec?,分别进行各自模糊规则表的查询;然后再对量化因子和决策因子进行修正,进而达到对整个模糊系统进行论域伸缩的目的;最后得到了一组PID参数的修正值ΔK?P、ΔK?I和ΔK?D,其中PID参数的优化值、初始值和修正值存在如下关系:

图2 变论域模糊PID控制器结构框图Fig.2 The structure of variable universe fuzzy PID controller
(4)
2.2 常规模糊PID控制器设计
以复合变速器的实际速比与目标速比的偏差e?和偏差变化率ec?作为输入变量,将它们的变化范围定义为模糊集上的论域,e?、ec?对应的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。定义3个输出语言变量,分别是比例修正值ΔK?P、积分修正值ΔK?I、微分修正值ΔK?D,对应的模糊子集分别如下式:
(5)
其中NB、NM、NS、ZO、PS、PM、PB分别代表负大、负中、负小、零、正小、正中、正大。
模糊规则是根据专家经验知识库得到的,根据K?P、K?I和K?D3个参数对系统动态特性的影响,可以得到比例、积分、微分常数修正值所建立的模糊规则表[11-12]。表1给出了ΔK?P的模糊修正表(ΔK?I和ΔK?D同理可得)。
利用MATLAB中的Fuzzy工具箱,选择控制器类型为Mamdani型,定义输入输出变量隶属函数的类型为三角型,在Fuzzy编辑器中输入49条模糊规则,设定非模糊化方法为重心平均法,可得ΔK?P随系统偏差e?和偏差变化率ec?的变化规律(ΔK?I和ΔK?D同理可得)。

表1 ΔKP的模糊修正表
2.3 基于量化因子和决策因子变论域的实现
对量化因子(K?e?和K?ec?)和决策因子(K?u?)伸缩实际就是对输入输出论域的一种伸缩。量化因子K?e?和K?ec?增加,系统输入论域收缩,输入e?和ec?对系统的作用就增大;反之,输入e?和ec?对系统的作用就减小。决策因子K?u?增加,系统输出论域扩张,模糊输出变量u?对系统的作用增大;反之,u?对系统的作用减小。对e?和ec?输入论域的伸缩只与自身变化有关,设输入e?和ec?论域的伸缩因子分别为α?和β?,它们对应的模糊子集为{B,M,S,ZE},得到输入论域伸缩因子的模糊规则如表2所示,其中B,M,S,ZE分别表示正大、正中、正小和零。
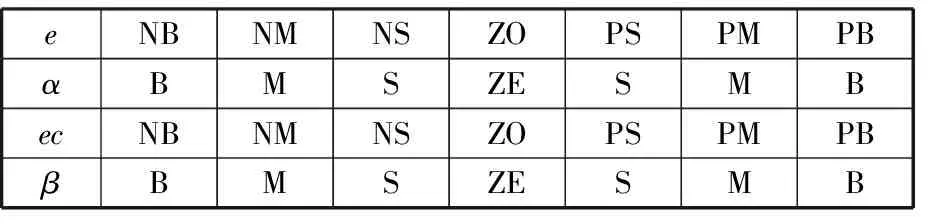
表2 伸缩因子α和β的模糊规则表
输出论域的伸缩需要根据反映系统状态的e?和ec?共同确定,当e?和ec?都较大且符号相同时,说明系统实际速比与目标速比相差较大,并且在逐渐偏离目标速比,使得误差进一步扩大,此时控制器需要增加输出,扩大输出论域以便让系统尽快回到目标速比附近。当e?和ec?都较大且符号相反时,说明系统实际速比与目标速比相差较大,但是正在以较快的速度回到目标速比附近,此时应该保持当前论域以防止系统出现振荡等问题。当e?较小、ec?较大时,说明实际速比与目标速比相差不大,但是将要以很快的速度偏离目标速比,此时应该适当扩大输出论域,增加输出量,使系统不会偏离目标值。设系统输出论域的伸缩因子为γ?,对应模糊子集γ?={ZE、VS、S、SB、M、B、VB},得到输出论域的伸缩因子γ?的伸缩模糊规则如表3所示,ZE、VS、S、SB、M、B、VB分别表示零、超小、正小、中小、正中、正大、超大。

表3 伸缩因子γ的模糊规则表
3 基于AMESim-MATLAB的联合仿真
3.1 液压机械无级变速器联合仿真模型
目前HMCVT系统模型的建立主要有3种工具,分别是功率键合图、MATLAB/Simulink和AMESim。功率键合图和AMESim都是基于功率流的建模工具,但是AMESim为用户提供了图形化建模的方式,可以让用户从繁杂的数学建模中解放出来[13]。MATLAB/Simulink对HMCVT建模需要对其简化,这样反而降低了模型精度,但是Simulink为用户提供了实用的控制算法工具箱[10]。综上分析,采用基于AMESim和MATLAB联合仿真方式。HMCVT模糊PID控制的AMESim和MATLAB联合仿真模型如图3所示,AMESim模型主要由发动机模型、行星排、泵-马达系统和负载模型构成。负载模型模拟了汽车行驶的过程,仿真模型的基本参数设置如表4所示。变论域模糊PID控制器和模糊PID仿真模型如图4、图5所示。
3.2 液压机械无级变速器速比跟踪仿真
为了验证模型的调速特性的正确性,建立了图6所示的HMCVT实验平台。该实验平台主要由动力输入装置、HMCVT和加载装置等构成,通过调节排量比的大小对复合变速器输出转速进行检测,其中实验平台的基本参数与仿真模型一致。排量比为0~1时,传动比变化的理论、仿真和实验曲线如图7所示。从图中可以看出,理论结果比仿真和实验结果偏高是因为理论计算时忽略了液压损失和机械损失,但是仿真速比变化基本与理论和实验速比变化吻合,由此验证了仿真模型调速特性的正确性。

图3 基于AMESim液压机械无级变速器联合仿真模型Fig.3 The simulation model of HMCVT based on AMESim

表4 仿真模型基本参数
在验证仿真模型正确性后,借助图3的仿真模型首先找到一组控制效果较好的PID参数(ΔK?P=8,ΔK?I=40,ΔK?D=0.02),为了便于比较本文设计的变论域模糊PID控制器与常规模糊PID控制器,使以上两个控制器的基本参数完全相同,观察两者在不同目标信号下的控制效果。

图4 变论域模糊PID仿真模型Fig.4 The simulation model of the variableuniverse fuzzy PID

图5 模糊PID仿真模型Fig.5 The simulation models of the fuzzy PID

图6 液压机械无级变速器实验平台Fig.6 The experiment platform of HMCVT

图7 理论、仿真和实验速比变化曲线Fig.7 Speed ratio curves of theory, simulation, experiment
3.2.1阶跃信号跟踪
以0.75的速比作为阶跃输入信号,负载不变。两种算法速比响应控制效果如图8a所示,速比跟踪误差如图8b所示,最大超调量和调整时间对比如表5所示。由以上数据分析可得,在阶跃信号跟踪中,变论域模糊PID控制较模糊PID控制超调量更小,调整时间更短,速比跟踪误差更小。

(a)速比跟踪比较

(b)速比跟踪误差比较图8 阶跃信号跟踪效果Fig.8 The follow-up control effect of step single input

控制算法最大超调量(%)调整时间(s)模糊PID4.41.3变论域模糊PID1.60.7
3.2.2斜坡信号跟踪
斜坡信号(速比变化范围为0~1.1)跟踪控制效果如图9所示。从图中看出,两种控制算法在斜坡上升跟踪阶段都存在跟踪误差,而且随着跟踪速比的增大而增大,在稳态阶段不存在稳态误差,在斜坡下降跟踪阶段存在跟踪误差,跟踪速比越小跟踪误差就越小。模糊PID控制的跟踪误差在(-0.06,0.075)范围内,而变论域模糊PID控制的跟踪误差在(-0.03,0.03)范围内,速比跟踪误差约降低了50%。

(a)速比跟踪比较

(b)速比跟踪误差比较图9 斜坡信号跟踪效果Fig.9 The follow-up control effect of ramp signal input
3.2.3正弦信号跟踪
设定频率为0.25 Hz, 速比变化范围为(0.1,0.9)的正弦信号输入,跟踪效果如图10所示。两种控制算法跟踪速比都存在一定滞后和误差,跟踪误差也呈正弦趋势变化。从图10b可以看出,变论域模糊PID控制的跟踪误差小于模糊PID的跟踪误差,速比跟踪误差降低了约50%。

(a)速比跟踪比较
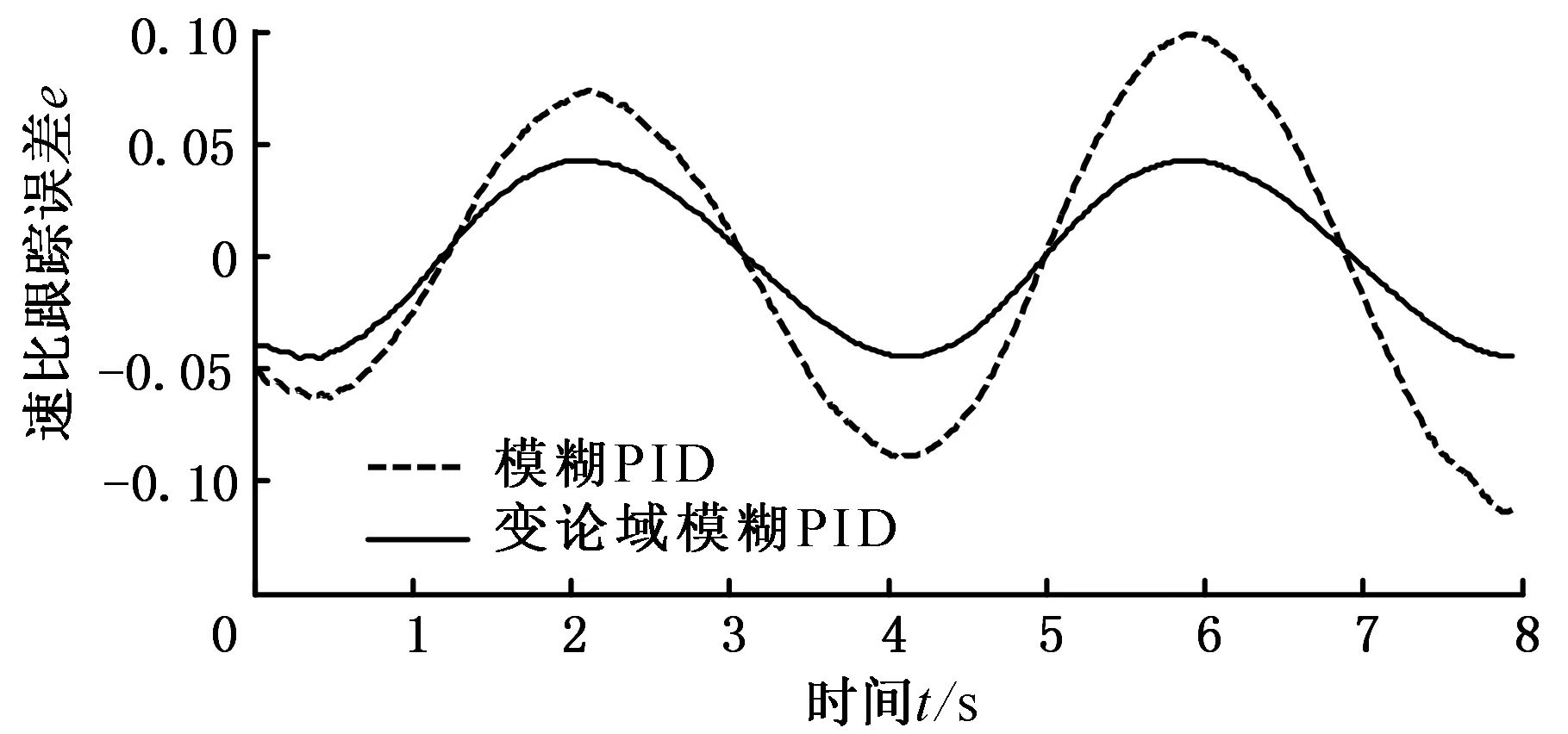
(b)速比跟踪误差比较图10 正弦信号跟踪效果Fig.10 The follow-up control effect of sine signal input
综上分析,变论域模糊PID控制器比常规模糊PID器的速比跟踪效果更好,速比跟踪误差更小,具有更优的动态响应特性,表现出更好的适应性和动态品质。
4 结论
(1)本文设计了一种输出耦合式液压机械无级变速器,分析了液压机械无级变速器的调速特性和系统数学模型,设计了一种基于量化因子和决策因子伸缩变化的变论域模糊PID控制器,分析了量化因子和决策因子在模糊PID控制中的作用,并制定了量化因子和决策因子伸缩变化的模糊规则表。
(2)搭建了基于AMESim和MATLAB的液压机械无级变速器联合仿真平台,通过实验平台验证了模型的正确性。在联合仿真平台上进行了阶跃信号、斜坡信号和正弦信号的速比跟踪测试,仿真结果表明:所设计的变域模糊PID控制器比常规模糊PID控制器速比跟踪控制效果更好,速比跟踪误差更小,表现出更优越的动态跟踪品质。研究结果为液压机械无级变速器控制策略提供了理论参考。

