径向弹簧蓄能密封结构最大接触应力的有限元分析

(北京航天发射技术研究所 北京 100076)

弹簧蓄能密封技术是一种新型的密封技术，典型的径向弹簧蓄能密封圈通常包括金属弹簧和非金属密封骨架两部分，工作时依靠内部金属弹簧提供向外的压紧力，作用于外部的非金属密封骨架实现密封。弹簧蓄能密封技术的研究计算涉及到流体力学、材料力学、摩擦学、高分子材料学以及机械制造工艺学等多方面的理论知识，其密封性能更是与密封面的表面状况、密封面材料、密封面宽度、密封比压、介质性质等多方面的因素有关[1-2]。其中通常所说的密封比压为密封面上的平均密封比压，是按整个密封面积平均计算的，而实际密封面上的最大接触应力值才是影响密封性能的关键。

目前，研究人员对径向弹簧蓄能密封进行了深入研究。耿志翔等[3]通过压缩试验对径向弹簧蓄能密封圈的变形和恢复性能进行了研究；贾晓红和李坤[4]分析了弹簧蓄能密封圈的密封性能，得到了接触区的压力分布特性。然而，针对径向弹簧蓄能密封结构最大接触应力的研究相对缺乏。

本文作者针对弹簧蓄能密封结构中影响较大的最大接触应力，结合典型的弹簧蓄能密封结构，首先分析径向弹簧张力密封结构的密封机制，以及O形弯曲金属螺旋弹簧的弹性特性；然后以此为基础，采用有限元的方法，以ANSYS仿真软件为工具，结合Excel数据处理软件进行部分后处理，对弹簧蓄能密封圈在不同压缩率、不同介质压力下的应力应变进行分析，研究其在多种工况下最大接触应力的变化情况，并对压缩率、介质压力与最大接触应力的关系进行了曲线拟合，可以用于指导弹簧蓄能密封结构的精确设计。

1 径向弹簧蓄能密封结构的密封机制

径向弹簧蓄能密封圈由O形弯曲的金属螺旋储能弹簧和非金属密封骨架组合而成，图1所示为典型径向弹簧蓄能密封圈的三维示意图，图2所示为将其装入密封槽时的工作示意图，其中p为介质压力。

图1 典型径向弹簧蓄能密封圈示意图

图2 弹簧蓄能密封圈的结构示意图

带压介质在压力的作用下外逸，外逸的介质沿着零件之间的缝隙扩散，逐渐到达密封圈位置，由于非金属密封骨架在预紧反弹性力的作用下紧贴被密封件的壁面，压力稍低的介质不能透过该屏障；随着外逸介质的增多，密封圈腔内的压力也逐渐上升，此时的密封圈在介质压力的作用下，其密封面也会更好地贴合在被密封件的密封面上；最终在预紧反弹性力和介质压力的综合作用下，在密封面上会产生足够大的接触应力，即密封比压，从而实现对结构的密封[5-6]。

工作时弹簧蓄能密封圈的密封接触应力主要由以下3部分组成：

(1)弹簧蓄能密封圈装配于槽腔后，非金属密封骨架结构本身相对于槽腔的过盈产生的接触应力p1；

(2)O形弯曲的金属螺旋弹簧在受到径向压缩时产生反弹性力，从而作用于密封圈而产生压紧力p2；

(3)介质内压作用于密封圈而产生的接触应力p3。

其中第一部分应力相比后两部分应力影响很小，可以忽略不计，也就是说，密封面上的密封比压q主要依赖于金属弹簧和介质内压的综合作用，即：

q=p2+p3

(1)

2 O形弯曲金属螺旋弹簧的弹性特性分析

O形弯曲金属螺旋弹簧由截面为矩形的钢带绕制而成，绕制完成后为竖直的圆柱螺旋弹簧，使用时将其首尾进行连接，再装入事先制作好的非金属骨架中，其受到径向压缩时的弹性力大小直接关系到密封比压的高低。该类型弹簧径向受力情况较为复杂，其力学特性在二维截面模型中较难表示，给仿真计算造成一定的困难。

空心金属O形圈一般用金属圆管弯制焊成，其弹性蓄能机制与O形弯曲金属螺旋弹簧有一定相似性。由于空心O形圈结构相对简单，其径向弹性力计算方法也相对成熟，下文主要对O形弯曲金属螺旋弹簧的径向刚度进行近似计算，并与金属O形圈的径向刚度进行对比分析，为接下来有限元模型的简化及建立提供依据[7-8]。

2.1 O形弯曲金属螺旋弹簧的径向刚度分析

处于直线状态的圆柱螺旋弹簧如图3所示，当受到径向挤压时，其结构受力具有一定的重复性，在此取一个螺距的弹簧按缺口环做近似分析，如图4所示。

图3 圆柱螺旋弹簧

图4 单圈弹簧的径向受力图

在此先做几点假设：

(1)不考虑螺旋角β的影响。螺旋角β本身比较小，对弹簧径向受力的影响也较小，但它的存在会大大增加计算的复杂性，故暂且将其忽略；

(2)假设弹簧片所用的金属材料为线弹性材料，即材料本身的应力和应变呈线性关系；

(3)假设径向压缩力Q均匀地作用在弹簧片横截面上，计算时将其作用点等效到横截面的形心处。

在此基础上，由载荷的对称性质，得出在对称界面上的剪力与转角均为0，故可取其中的1/4圈进行受力分析，如图5所示。

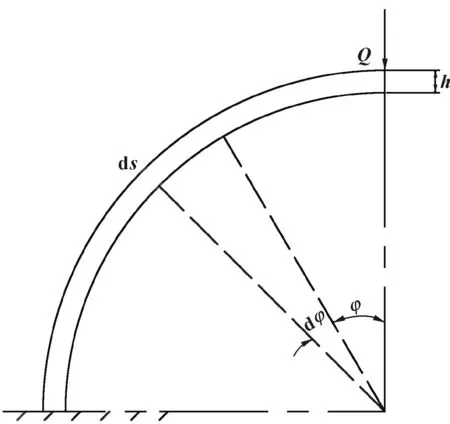
图5 1/4圈弹簧的等效受力图

结合其结构特点，按照材料力学中曲杆受力的方法对其进行分析，根据莫尔定理来计算其径向位移，考虑到受力过程中弹簧不受扭，则：

ε1=∫S0MMdsEI

(2)

式中:ε1为弹簧的径向位移；M为任意截面上单位力产生的弯矩；M为任意截面上作用力Q产生的弯矩；E为弹簧材料的弹性模量；I为弹簧界面的惯性矩。

弹簧任意截面上单位力产生的弯矩为

M(φ)=Rsinφ

(3)

将公式(3)代入公式(2)，注意到ds=Rdφ，可求得1/4圈弹簧的压缩变形量为

ε1=1EI∫π/20Rsinφ·QRsinφRdφ=πQR34EI

(4)

式中:Q为弹簧所受径向力；R为弹簧的半径。

弹簧片截面为矩形，则其截面惯性矩为

I=bh312

(5)

式中:b为弹簧片的宽度；h为弹簧片的厚度。

将公式(5)代入公式(4)，即得：

ε1=πQR34EI=3πQR3bEh3

(6)

从而一个螺距弹簧的变形量为

σ1=2ε1=6πQR3bEh3=3πFR3bEh3

(7)

则一个螺距弹簧的径向刚度近似为

Fσ1=bE3π·(hR)3

(8)

2.2 与金属O形圈弹性特性的对比

为了对比O形弯曲金属螺旋弹簧与空心O形圈的弹性特性，选择一个材料、壁厚、直径均相同的金属O形圈，在相同的载荷作用下作变形分析。为方便计算与对比，选择宽度为b的截面段，其受力情况如图6所示。

图6 金属空心O形圈密封结构图

运用材料力学中的方法，结合卡氏定理，可得该段O形圈的变形量为

σ2=(π4 - 2π)FR3EI=(3π - 24π)FR3bEh3

(9)

对比螺旋弹簧与金属O形圈在相同情况下的径向刚度：

ξ=Fσ1Fσ2=σ2σ1=3π(3π - 24π)=5.3

(10)

可以看出，在材料、壁厚、直径以及载荷均相同的情况下，空心金属O形圈的近似径向刚度为O形弯曲金属螺旋弹簧的5.3倍。由于前期的假设条件会导致计算所得的O形弯曲金属螺旋弹簧径向刚度较真实值偏大，故空心金属O形圈与O形弯曲金属螺旋弹簧的真实径向刚度比值应大于5.3。

3 径向弹簧蓄能密封结构的有限元模型

3.1 建立坐标系

典型的弹簧蓄能密封结构在结构上是轴对称的，在理想情况下，弹簧蓄能密封圈沿轴线方向的载荷也是对称的。由于载荷和结构的对称性，弹簧蓄能密封圈的密封属于轴对称问题[9-10]。

因此，可以把此问题简化成二维问题进行研究，其中任意一点的应力、应变及变形只与坐标x和y有关，与其在周向的位置无关，所以只需研究坐标平面xOy上的截面部分，取其过回转轴线的一个剖面建立坐标系，如图7所示。

图7 弹簧蓄能密封结构的计算坐标系

由于弹簧蓄能密封圈的位置关于y轴对称，所以取模型的右半部分进行研究，该剖面的力学行为在理想情况下是能够反映弹簧蓄能密封圈的力学行为的。弹簧蓄能密封圈的密封行为主要发生在其内外圈表面分别与内密封面和外密封面的接触面上，所以，建立模型求解的目的主要是为了了解弹簧蓄能密封圈内圈表面——被密封件1，以及弹簧蓄能密封圈外圈表面——被密封件2这两组密封副上的接触应力分布。

3.2 有限元模型的建立

弹簧密封圈的主要设计尺寸如图8所示。

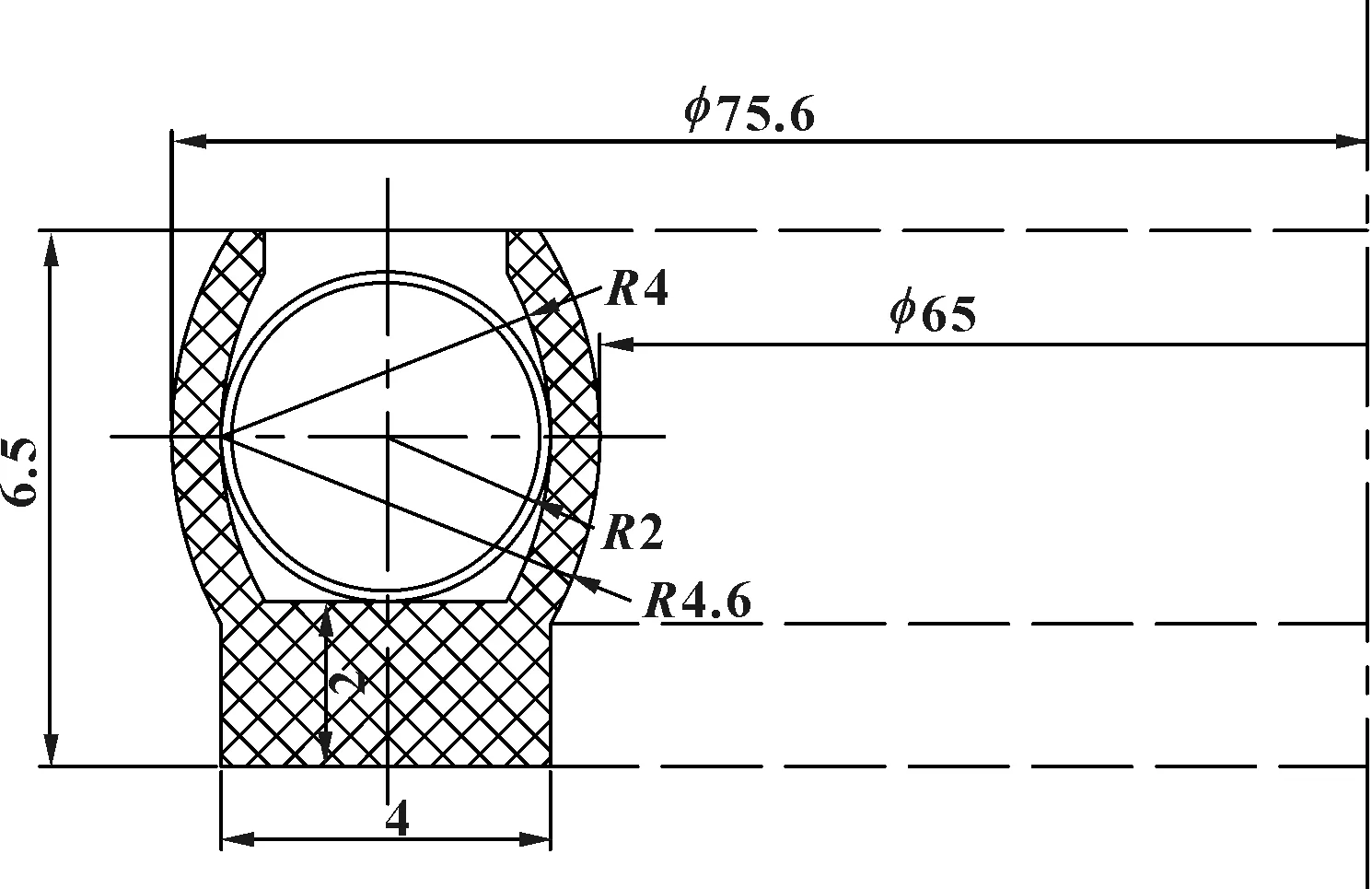
图8 弹簧蓄能密封圈的结构尺寸

结合2.2章节中的分析，金属螺旋弹簧的径向刚度近似表达式与金属O形圈的径向刚度表达式类似，应力应变关系均表现出一定的线性特征，仅有系数的差别，考虑到其力学性能有一定的相似性，文中在二维模型中以金属O形圈代替弹簧来进行仿真。同时为方便计算，将模型中金属O形圈材料的弹性模量作降低一个数量级处理，即金属O形圈的弹性模量本身为2.1×105MPa，在模型中将其设定为2.1×104MPa，以尽量接近O形弯曲金属螺旋弹簧的真实弹性特性。

图9所示为构建的有限元模型，其中省略了部分内密封面和外密封面的材料，但并不影响计算分析，因为弹簧蓄能密封圈的作用主要发生在其与内、外密封面的接触面上。

图9 弹簧蓄能密封结构的有限元模型

如图9所示，该模型中包含有较多的接触关系，在计算时会占用较多的计算机资源，考虑到弹簧蓄能密封圈在密封槽中完成预紧装配时，其结构及受力具有一定的对称性，因此文中取模型的右半部分进行分析，如图10所示。

图10 弹簧蓄能密封结构的网格模型

简化后的有限元模型可以在不影响计算分析的情况下，有效地模拟密封副上的压力特性，并对非金属密封骨架的应力集中点进行分析。该模型采用四节点平面单元PLANE182进行网格划分，另外对密封面上的网格单元进行单独的加密处理。

3.3 材料模型的选择

非金属密封骨架的材料设定为聚四氟乙烯，金属弹簧的材料设定为弹性合金，外密封面的材料设定为铝合金。假设上述3种材料分别为材料1、材料2和材料3，分别对其弹性模量和泊松比作如下设定：E1=2.1×104MPa，μ1=0.3，E2=1.2×103MPa，μ2=0.4，E3=2.1×105MPa，μ3=0.3。

3.4 接触算法

ANSYS通常使用的接触算法有：罚函数法、拉格朗日算法、扩张拉格朗日算法。其中扩展拉格朗日算法是不停更新接触刚度的罚函数法，这种更新不断重复，直到计算的穿透值小于允许值为止。其优点是与罚函数法相比较少病态，各接触单元的接触刚度取值更合理，与单纯的拉格朗日算法相比，可以避免使主对角线系数为0。因而文中选择扩展拉格朗日算法作为接触算法。

模型中主要有2个接触对：弹簧与非金属密封骨架内壁的接触，非金属密封骨架外壁与被密封面的接触。这2个接触对均由接触单元CONTA172和目标单元TARGE169配对组成，接触面上的摩擦模型选择为库仑摩擦类型，摩擦因数设置为0.1。

3.5 边界条件与加载方式

在图11所示的有限元模型中，考虑到结构和受力的对称性，将金属弹簧截面的转角为零作为变形协调条件，约束弹簧两个截面上x方向的自由度，对非金属密封骨架的截面约束所有方向上的自由度，底面约束y方向上的自由度，如图7所示。

图11 增加边界条件之后的有限元模型

具体的加载过程可以分3个载荷步进行：

(1)将被密封件2沿y轴正方向移出一定距离，使其与非金属密封骨架不接触，紧接着对其施加一定的y轴负向位移，缓慢移动至其安装位置，模拟其在不同压缩量下的工作情况；

(2)在弹簧蓄能密封圈的内腔施加不同压力，模拟其在不同介质压力下的工作情况。

4 计算结果及分析

为了研究弹簧蓄能密封圈在不同压缩量、不同介质压力下的密封特性，文中共模拟了4种压缩率(5%，10%，15%，20%)下的弹簧蓄能密封圈在5种不同介质压力(0，0.2，0.5，0.8，1.2 MPa)下的接触应力。

以介质压力1.2 MPa为例，图12示出了不同压缩率下的接触应力云图。不同工况仿真计算结果汇总如表1所示。

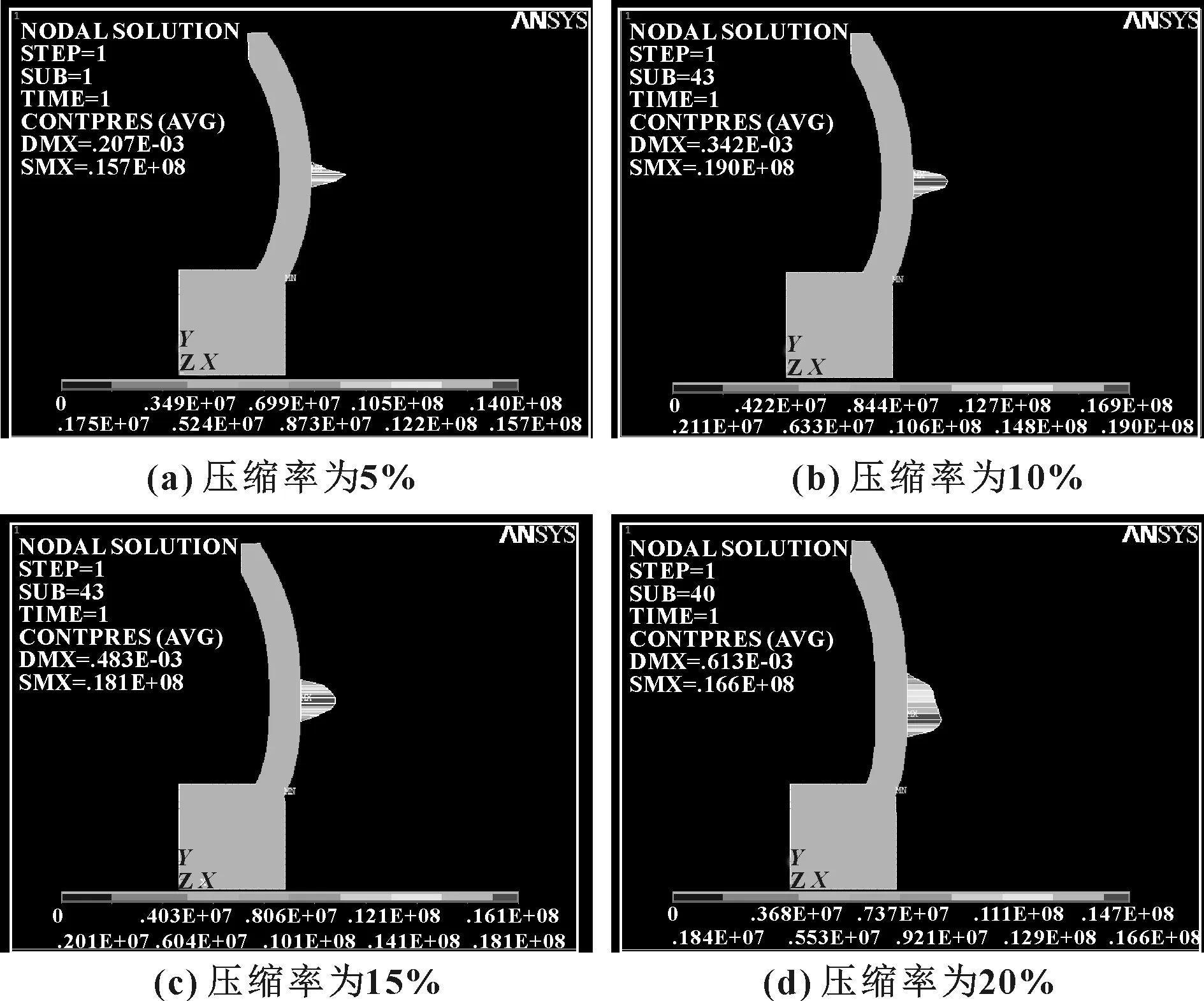
图12 介质压力为1.2 MPa时不同压缩率下的接触应力分布 云图

压缩率ε/% 最大接触应力pmax/MPa 0 MPa0.2 MPa0.5 MPa0.8 MPa1.2 MPa512.313.314.414.915.71015.516.117.618.2191516.716.917.217.518.12014.414.815.315.916.6

将表1中的汇总结果用Excel软件作统一整理，即可得到不同压缩量、不同介质压力下的最大接触应力，如图13、图14所示。

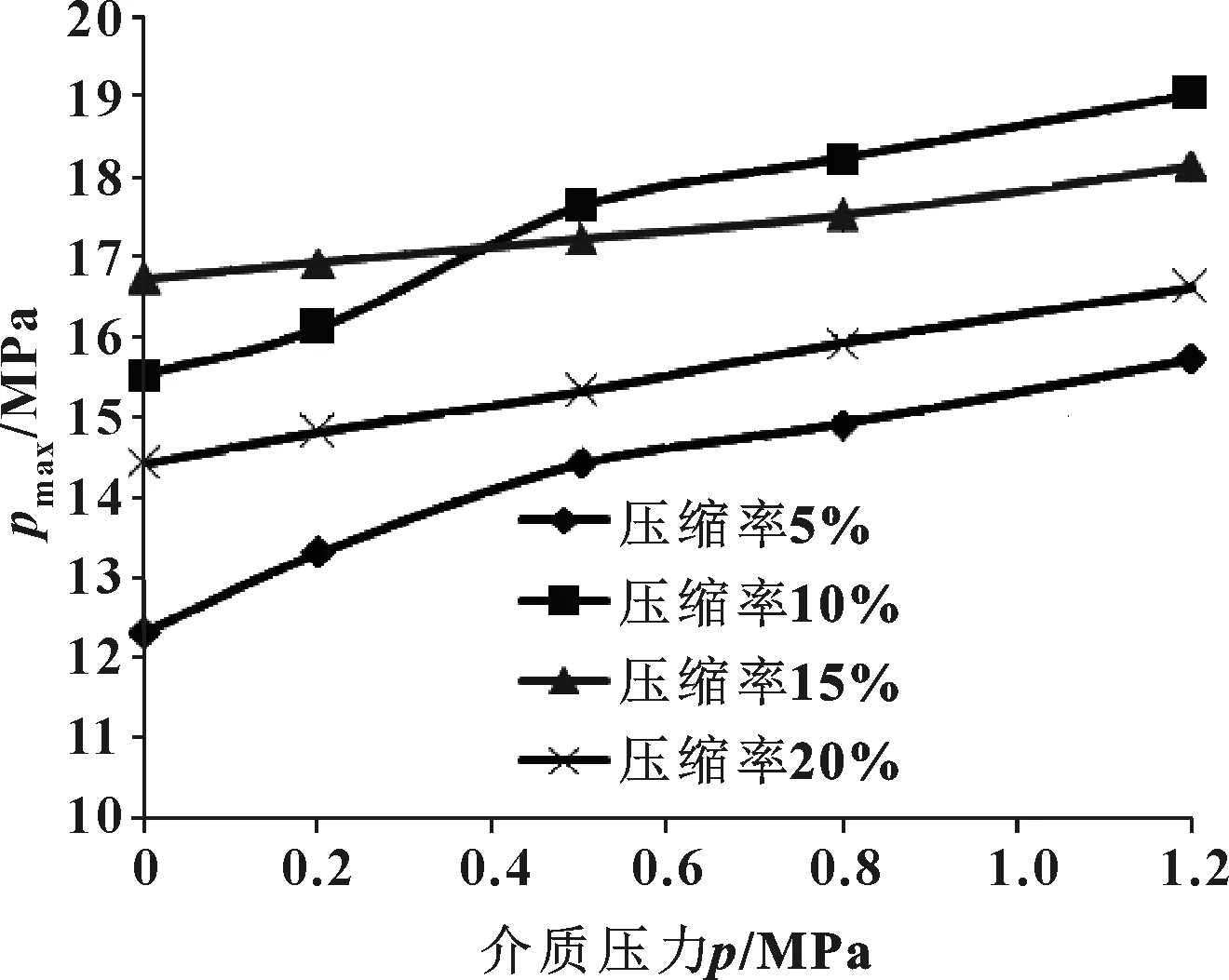
图13 不同压缩率下，最大接触应力与介质压力的关系曲线

图14 不同介质压力下，最大接触应力与压缩率的关系曲线

从图13、图14中可以看出：

(1)当压缩率一定时，弹簧蓄能密封圈与密封接触面上最大接触应力均随着介质压力的增大而增加，且基本呈现出一定的线性关系；

(2)当介质压力一定时，密封面上的最大接触应力会先随着压缩率的增大而增大，待达到一定峰值之后再随着压缩率的增大再减小，且峰值所对应的压缩率会随着介质压力的不同而有所变化。

考虑到弹簧蓄能密封圈本身的结构特点，导致上述结果的主要原因是：随着压缩率的增大，金属弹簧在非金属密封骨架上的弹性力作用点有上移趋势；与此同时密封面的宽度会随之增大，密封面上的接触应力分布也更加均匀，且该趋势会随着压缩率的增大而逐渐变强，因而密封面上的最大接触应力会先随着压缩率的增大而增大；在压缩率大于一定值后，由于密封面宽度增大的趋势相对更快，因而密封面上的最大接触应力会出现峰值，然后随着压缩率的增大而有所减小。

5 压缩率、介质压力与最大接触应力的拟合曲线

从图13中可以清晰地看出，不同压缩率的弹簧蓄能密封圈的最大接触应力均基本随着介质压力的增大而呈线性增长趋势，区别为不同压缩率下曲线的一次函数斜率和截距不同，这也为描述某一特定介质工作压力下弹簧蓄能密封圈最大接触应力与压缩率的关系提供了一种参照。

定义该一次曲线的的斜率为η1，称其为应力影响系数，介质压力用p表示，而不同压缩量的弹簧蓄能密封圈在压缩量为0时的常数，也就是该一次曲线的截距，用常数C1来表示，于是此描述弹簧蓄能密封圈压缩率、介质压力与最大接触应力的关系曲线可以表示为

pmax=η1p+C1

(11)

对上述4种压缩率下的一次曲线均进行一次拟合，不同压缩率下曲线所对应的斜率和截距均不相同，绘制出斜率、截距以及压缩率关系曲线如图15所示。

图15 弹簧蓄能密封圈的压缩率和常数关系曲线

由图15可以方便地计算出压缩率在5%～20%之间的弹簧蓄能密封圈在不同介质压力下的密封面最大接触应力pmax。根据公式(11)，要计算最大接触应力，只需要知道介质压力p，应力影响系数η1以及参数C1，其中工作压力p由实际工况决定，应力影响系数η1以及常数C1均可由图15查得。

6 结论

(1)当介质压力一定时，密封面上的最大接触应力会先随着压缩率的增大而增大，待达到一定峰值之后再随着压缩率的增大再减小，且峰值所对应的压缩率会随着介质压力的不同而有所变化。这种情况可以用于指导在流通介质以及工作压力已经确定的情况下，弹簧蓄能密封结构的设计。

(2)当弹簧蓄能密封圈的压缩率一定，也就是密封结构已经固定时，密封面上的最大接触应力随着介质压力的增加而增大，且基本呈现出线性关系。这种情况可以用于评估弹簧蓄能密封结构的性能，考察其在不同介质压力下的密封表现。

(3)获得了密封面最大接触应力与弹簧蓄能密封圈压缩率、介质压力的关系曲线，并通过曲线拟合得到了一般情况下计算最大接触应力的数学表达式，绘制了与之对应的关系图，可以方便地进行参数查找。