动静压耦合效应下气体轴承流场特性分析*

(大连海事大学船舶与海洋工程学院 辽宁大连 116026)

静压气体轴承作为一种广泛应用在高速主轴上的支承方式，其高速特性直接影响加工精度和效率，因此对其高速特性的分析尤为重要。张广辉[1]针对经典混合气体轴承设计，建立了含小孔节流项的动静混合径向气体轴承可压缩气体润滑雷诺方程，通过牛顿迭代法和有限差分法实现了混合轴承动静压参数耦合求解。但他仅将动压性能参数与静压性能参数分别计算后进行叠加，忽略了动静压之间的相互影响的问题。郝艾鹏和贾玉红[2]通过对高速气浮轴承内部流场的仿真分析，探讨轴承转速、偏心率对气浮轴承动静压耦合效应的影响。结果表明，基于有限体积法的三维模型可有效地模拟动静压气浮轴承的内部流场，并与实际情况更加吻合。王彬[3]对超高速磨削实验台中的液体动静压混合轴承进行仿真分析，分析不同转速时油膜的压力分布、承载力和温度场分布特性。于贺春[4]通过旋转坐标系与静态网格相结合的方法实现静压气体轴承动态特性的三维计算。分析了动压效应对轴承的主承载能力及刚度的影响，结果表明，偏心率越大，动压效应越明显。杨文勇和马平[5]定性分析了空气静压轴承气膜动刚度在主轴高速运转中所表现的非线性行为。高思煜[6]研究不同转速和偏心率工况下空气静压径向轴承和止推轴承的结构参数对轴承压力分布、承载力等性能的影响规律。LO等[7]通过假设轴承间隙和小孔处的流量相等，得到了非线性量纲一化气体润滑雷诺方程，进行求解后获得了压力分布、摩擦力、承载力和流量等。SU和LIE[8]研究了多排小孔供气混合径向轴承的旋转效应，得到轴承承载能力伴随偏心率的增加而增加，且增加速率快于其伴随转速的增加速率的结论。于贺春等[9-10]基于Fluent软件，通过改变气膜厚度、节流孔(缝)深度，对比研究了狭缝节流和微孔节流静压气体止推轴承的承载力、刚度及耗气量；对轴承的总节流面积取不同值时的轴承特性进行分析对比，从而判断了两种轴承在一定条件下是否具有互换性；分析了微孔节流气体静压止推轴承的供气孔数目、供气孔分布半径和供气孔直径对轴承静态特性的影响规律。

本文作者以高速静压气体轴承为研究对象，在不同偏心率及转速条件下对流场特性、动静压耦合效应机制、承载力以及偏心角进行分析研究。

1 基于有限体积法的数值仿真

1.1 几何建模

图1所示为环形静压气体轴承的结构，采用简单孔式供气，节流孔沿圆周方向均匀分布，轴承的基本参数如表1所示。

图1 静压气体轴承结构

参数数值轴承长度L/mm60轴承直径D/mm50节流孔直径d/mm0.25平均气膜间隙h0/mm0.028两排进气孔距离L1/mm30节流孔与端面距离l/mm15每排节流孔数n12节流孔排数2

将气体轴承流场沿轴向分为三类区域，区域L1为气体流动的止滞区域，区域l为气体流向大气的过渡区域，区域L2为进气孔影响区域。由于止滞区域L1的轴向流动可以忽略，并且静压气体轴承气膜厚度h0较小，气体轴承存在偏心距时，气体轴承流场圆周方向存在楔形空间，因此可将气体在区域L1的圆周方向流动假定为一维倾斜平板的流动。由于气体流速沿气膜法向(气膜厚度方向)的梯度极大，忽略体积力(如重力与惯性力)的影响，只考虑流速沿气膜高度h方向梯度所引起的黏性力，且黏性力与正压力互相平衡。静压气体轴承的转子高速旋转时，气体流动沿气膜高度的分布规律速度u符合公式(1)[11]。

u=U(1-zh)- (∂p∂x)z(h-z)2μ

(1)

式中：u为气体流速,m/s；U为平板速度,m/s；h为平板间隙,m；z为气膜法向高度,m；∂p∂x为平板速度方向的压力梯度；μ为动力黏度,Pa·s。

1.2 网格划分及边界条件设定

根据静压气体轴承结构参数建立三维仿真模型及边界条件设置如图2所示。

图2 静压气体轴承三维模型

由于对称性，文中采用1/2对称模型进行分析，可减少网格划分工作量，缩短计算时间。对模型分区划分结构化和非结构化网格，对节流孔及其影响区域进行网格密化，以提高解算精度和速度。

(1) 边界条件设置：将节流孔进气边界设置为压力入口(Pressure-Inlet)；流体计算域排入大气端面设置为压力出口(Pressure-Outlet)，在压力出口边界上p=p0；轴承对称面设置为对称边界(Symmetry)；转子壁面设置为旋转壁面(Moving-Wall)。

(2) 计算模型设置：选择离散、隐式求解器；湍流模型选择SSTk-ω模型，是由于其比标准k-ω模型在广泛的流动领域中有更高的精度和可信度，特别是在旋转流动中可以体现出更大优势；采用应用较为广泛的基于速度与压力相互耦合原理的SIMPLE算法；压力项选择PRESTO，以解决供气孔处节流之后压力和梯度突变。

1.3 网格无关性验证

网格数量和质量影响数值仿真结果的准确性，当网格数量较少时，会影响数值仿真的整体计算结果，降低计算精度；而增加网格数量虽可以提高的计算精度，但同时也会增加网格划分和计算时间。因此，在不降低计算质量的条件下，应控制网格数量，提高计算效率。

如表2和图3所示，77万网格数量时的承载力大于其他两种网格数量时的承载力，这是由于网格数量较少，无法精确捕捉节流孔附近压力陡降现象，造成77万网格时的流场模型整体的压力分布高于其他结果。120万网格数的节流孔附近压力分布及承载力的计算结果与200万网格数相差不大。考虑计算效率和网格数对数值仿真结果的影响，文中采用120万网格数进行数值仿真。

表2 不同网格数条件下承载力对比

图3 不同网格数量条件下节流孔附近压力分布

2 静压气体轴承仿真结果分析

2.1 流场压力分布特性分析

在偏心率ε=0.5，供气压力ps=0.6 MPa条件下，计算得到的流场止滞区圆周方向的压力分布如图4所示。其中0°和360°为最大气膜厚度处，气膜厚度h=0.042 mm，180°为最小气膜厚度处，气膜厚度h=0.014 mm。

图4 不同转速条件下圆周方向压力分布

研究结果表明：当转速升高，流场出现了圆周方向的高压中心与偏心方向偏转角度β。当转速n<40 000 r/min，β随转速升高由0°递增到9.66°，分析原因：气体黏性力起主导作用，气体由大间隙向小间隙流动的过程中，所表现出的动压效应与一维倾斜平板间流动的动压效应相比，流场静压力逐渐增大，压差流阻碍了气体流动，造成气体流速u减缓，流场压力升高；而气体由小间隙流向大间隙流动的过程中，流场静压力逐渐降低，受气体黏性力和压差流共同影响，造成气体流速u增加，压降速率增大；气体的这两种不同流动状态，产生了不同的动静压相互耦合效应。转速升高导致气体可压缩性的影响越来越明显，当转速n>40 000 r/min时，β随转速升高从9.66°递减到5.15°，圆周方向的高压中心朝气膜最小间隙h=0.014 mm位置偏转。

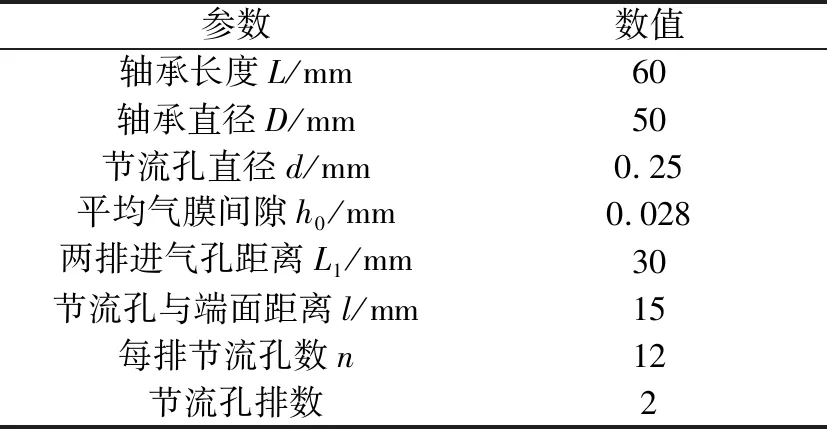
图5所示为流场止滞区圆周方向气体密度分布。从图4、图5可看出，随转速升高动静压耦合效应导致气体由大间隙流向小间隙流动时压力峰值由0.237 7 MPa逐渐增大到0.574 3 MPa，气体被压缩；气体由大间隙流向小间隙流动时，气体流速激增，压力梯度和密度梯度随转速升高而增加。

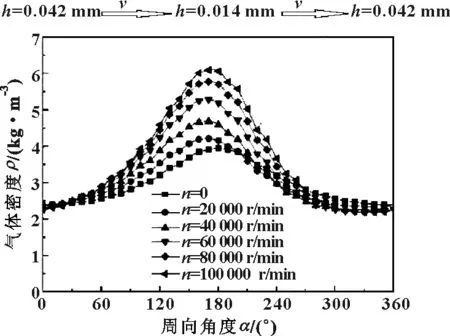
图5 不同转速条件下圆周方向气体密度分布

图6所示为不同转速下圆周方向节流孔附近压力分布。研究结果表明：在动静压耦合效应的影响下，气体流动速度u与转子转速正相关；当气体沿圆周向节流孔位置流动时，压力梯度∂p/∂x为负值；当气体沿圆周由节流孔位置流出时，气体流动速度与压力梯度∂p/∂x为正值。

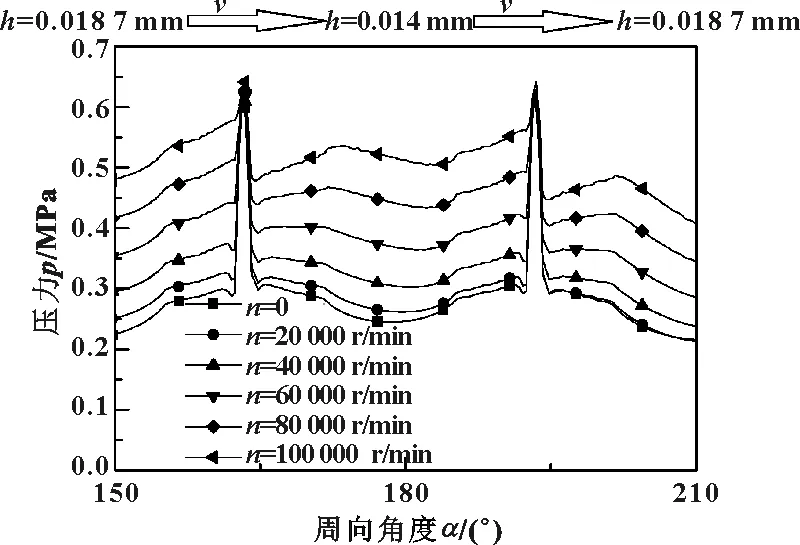
图6 不同转速条件下节流孔位置圆周方向压力分布

因此，当气体沿圆周向节流孔位置流动时，气体流速降低，节流孔附近压力陡降现象减弱；当气体沿圆周方向由节流孔位置流出时，气体流速升高，节流孔附近压力陡降区域沿周向延伸。节流孔周围的动静压耦合现象随转速升高而更为显著。

图7所示为不同转速条件下流场压力云图。对比发现，流场止滞区域L1圆周方向的高压区中心线与气膜最小间隙h=0.014 mm存在夹角，n<40 000 r/min时，夹角随转速升高由0°逐渐增大到17.65°，n>40 000 r/min时，夹角随转速升高由17.65°逐渐减小到12.89°，止滞区为主要承载区域，这种现象势必造成转子的偏心方向和承载力W方向存在偏心角φ。

图7 不同转速条件下流场压力云图

在n=60 000 r/min和供气压力ps=0.6 MPa的条件下，不同偏心率对流场的气体止滞区域的周向压力分布的影响如图8所示。随着偏心率的增大，周向压力峰值逐渐增大，压力峰值与最小间隙之间的夹角β逐渐减小。分析原因：偏心率的增加使得气体静压力逐渐增大，从而导致了静压力在流场压力的重新分布过程中占据主导地位，最终造成夹角β逐渐减小。

图8 不同偏心率条件下流场的周向压力分布

2.2 轴承承载力及偏心角特性分析

如图9所示，Wn为转子偏心方向承载力，气体静压轴承高速条件下的动静压耦合效应导致流场高压中心线与转子偏心方向之间存在偏心角φ，必然存在承载力Wt与Wn垂直，W为Wt与Wn合力,与载荷F等值反向。F、W、Wn、Wt满足式(2)。

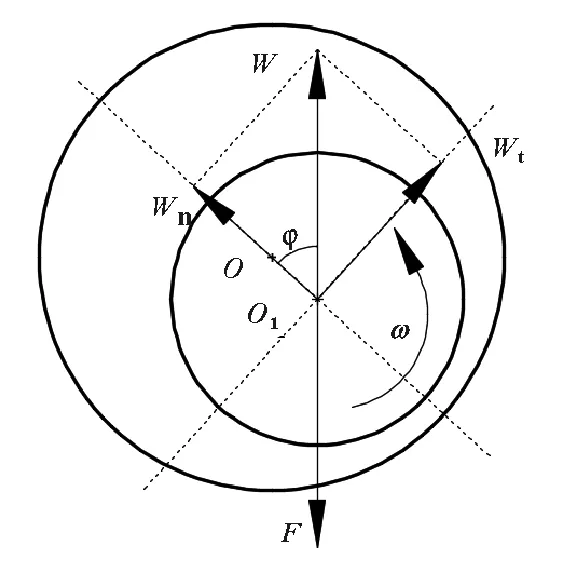
图9 静压气体轴承承载力、偏心角

{W=W2t+W2n

Wt=Wntanφ

(2)

图10所示为不同转速和偏心率条件下承载力的变化规律。研究结果表明：相同偏心率条件下，受动静压耦合效应和气体压缩性的共同影响，承载力随转速升高而单调递增；在相同转速条件下，偏心率的增加导致静压的压差增大和动静压耦合效应增强，从而使得承载力随着偏心率的增大而单调递增。

图10 不同偏心率及转速条件下承载力变化

图11所示为不同转速和偏心率条件下偏心角的变化规律。在相同的偏心率条件下，偏心角随转速升高呈非线性变化；转子保持低速(n<40 000 r/min)范围时，偏心角随转速升高而递增。分析原因，低速时气体的可压缩性表现不明显，动压效应使得流场的周向压力分布不均匀，导致偏心角不断增大。转子保持高速(n>40 000 r/min)范围时，偏心角随转速升高而递减，这是由于转速升高导致气体的可压缩性增强，使得气体进一步向最小间隙压缩，造成偏心角减小。

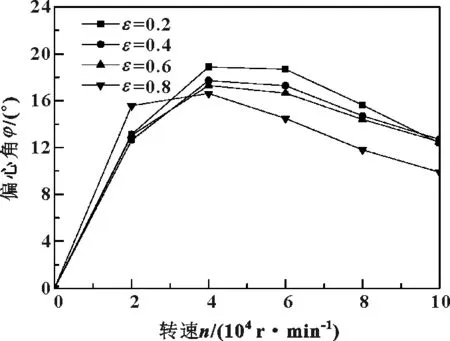
图11 不同偏心率及转速条件下偏心角变化

在相同的转速条件下，高速时偏心角随着偏心率的增大而减小。分析原因，偏心率增大造成静压效应增强；同时，由于流场圆周方向气膜厚度变化率|∂h∂α|增大，从而造成动静压耦合效应增强，高压中心向气膜最小间隙位置靠近，导致承载力Wn增大和偏心角的减小。当n=20 000 r/min时，偏心角随偏心率的增大呈现非单调变化趋势。究其原因，ε<0.8时，低转速条件下的气体可压缩性的影响较弱，而偏心率增加造成动静压耦合效应增强，流场的周向不对称现象逐渐明显，最终导致偏心角随着偏心率增加而逐渐增大；当ε>0.8时，因为静压力占据主导地位，造成周向压力分布不对称性现象减弱，使得偏心角减小。

3 结论

(1) 气体动静压耦合效应及强度受气体黏性力、压差流和压缩性共同影响。低转速(n<40 000 r/min)时，气体黏性力和压差流起主导作用，偏心角φ随转速升高而逐渐增大，高转速(n>40 000 r/min)时，气体压缩性影响随转速升高而逐渐增强，从而导致偏心角逐渐减小。而偏心率的变化造成静压效应和周向气膜厚度变化率的变化，从而引起流场压力分布和动静压耦合效应的改变，最终对气膜的承载力和偏心角的变化规律产生影响。

(2)由于气体黏性力和压缩性影响，气体向气膜最小间隙处流动并逐渐被压缩，高速旋转时压缩性增强，导致承载力随转速升高而增大，偏心率较大时(ε>0.4)，转速对承载力提高有显著影响。

(3)偏心率引起的流场压力分布状态改变会影响偏心角变化规律。研究发现，偏心角随转速变化规律不具有单调性：低转速(n<40 000 r/min)时，偏心角随偏心率增大而单调递增；高转速(n>40 000 r/min)时，偏心角随偏心率增大而递减。