转子-轴承-干气密封系统轴向振动稳定性分析*
(兰州理工大学石油化工学院 甘肃兰州 730050)
干气密封气膜之间的轴向平衡间隙为微米级尺寸[1],当微小的干扰作用于稳定运行的平衡状态密封端面,就会在平衡位置产生复杂的运动叠加。目前,干气密封技术不断完善,有超过90%的新型离心压缩机装备了干气密封[2]。密封一旦失效,引起介质泄漏不仅由于停车维修,造成巨大的经济损失,而且严重的会引起重大安全事故。因此,保证干气密封装置的稳定性、可靠性一直都是国内外研究的热点和难点。
ZIRKELBACK和ANDRES[3]采用微扰法,基于有限元法求解了扰动雷诺方程,得出了微扰频率的刚度和阻尼系数,并对其密封运动的稳定性进行了讨论。刘雨川[4]从轴向和角向方向上,采用有限元法求解微小扰动下的雷诺方程,迭代解出干气密封气膜的动态特性系数,作为气膜稳定性的判断依据。MILLER和GREEN[5]从轴向和角向两个方向上分析螺旋槽干气密封的密封环的振动情况,并且运用数值频率响应法计算出密封气膜的刚度和阻尼系数。李双喜等[6]对微扰雷诺方程采用了一种新的高阶形函数有限元法,获得了气体密封轴向微扰的刚度和阻尼。杜兆年、丁雪兴等[7-8]对部分气膜动态特性参数(1轴向、1角向),运用微扰法、近似解析法进行了计算论证。张伟政等[9]采用四阶的Runge-Kutta求解了气膜与静环的振动微分方程,并且探讨了不同槽型参数对密封系统中静环振动的影响规律。刘蕴等人[10]针对干气密封中气膜厚度稳定性,运用Workbench中的模态分析法和谐响应分析对浮动环系统进行研究,总结了不同参数条件下浮动环轴向振动幅值的变化趋势,并对影响其轴向振动幅值的主要因素和次要因素作了分析。丁雪兴等[11]建立了气膜-密封环系统轴向振动模型,考虑热耗散变形下的干气密封系统,在轴向上进行振动稳定性动力学分析。成玫等人[12]对转子-轴承-密封系统的非线性振动特性进行研究,选择的密封系统是迷宫密封。
目前,尽管在干气密封动力学研究方面已取得了不少成果,但关于干气密封应用大系统下的非线性动力学方面的理论研究还很少,有待于进一步分析研究。以转子、轴承、干气密封系统组成的大系统为研究对象时,考虑到实际的干气密封系统会同时受到密封力和轴承油膜力的影响,这两种因素之间会发生一定程度的耦合以及多频激励,从而导致复杂的动力学响应。本文作者研究转子-轴承-干气密封系统的非线性动力学行为,探讨在实际工况下干气密封槽形参数的稳定范围,归纳失稳的判据,对干气密封优化设计与实际应用具有重要的理论指导意义。
1 单自由度干气密封轴向振动计算模型
在恒定转速下(转速n=16 500 r/min),当不考虑转子、轴承,只考虑气膜和静环时,可建立如图1所示的气膜-静环系统轴向振动模型。图中:m2为静环质量;K2为气膜刚度;K3为弹簧刚度;C2为气膜阻尼;z为静环振动位移;F(t)表示作用在离散质量上的简谐激振力,其大小为Fi(t)=Pisin(ΩT+τ)。
其振动方程为
m2z··+C2z·+K2z+K3z=F(t)
(1)

图1 气膜-静环系统轴向振动模型
2 双自由度模型与基本方程的建立
2.1 转子-轴承-干气密封系统轴向振动模型
模型的假设:在恒定转速下(转速n=16 500 r/min),将转子-轴承-干气密封系统视为双自由度受迫振动;干气密封气膜可以假定为具有非线性刚度的弹簧;瞬态激振力假定为简谐激振力,其轴向位移可假定为简谐运动。
建立转子-轴承-干气密封系统几何模型如图2所示,其轴向振动模型如图3所示。

图2 转子-轴承-干气密封系统
图中:m1为动环和转轴的质量;m2为静环的质量;K1为轴承刚度;K2为气膜刚度;K3为弹簧刚度;C1为轴承阻尼;C2为气膜阻尼;x1为动环振动位移;x2为静环振动位移;F1(t)和F2(t)分别表示作用在两个离散质量上的简谐激振力,其大小为Fi(t)=Pisin(ΩT+τ)。
2.2 转子-轴承-干气密封系统轴向振动计算
由图3,根据牛顿定律分别写出两个离散质量的运动方程:
{F1(t)-K1x1+C2[x·2-x·1]+K2[x2-x1]=m1x··1
F2(t)-C2[x·2-x·1]-K2[x2-x1]-C3x·2-K3x2=m2x··2
(2)
整理得到:
{m1x··1+(C1+C2)x·1-C2x·2+(K1+K2)x1-K2x2=F1(t)
m2x··2-C2x·1+C2x·2-K2x1+(K2+K3)x2=F2(t)
(3)
为简洁,引入矩阵形式表达:
[C1+C2-C2
-C2C2]=[C],[K1+K2-K2
-K2K2+K3]=[K],{x}={x1
x2},{F(t)}={F1(t)
F2(t)},[m10
0m2]=[m]
可将运动方程写成简洁的矩阵形式:[m]{x··}+[C]{x·}+[K]{x}={F(t)}
引入量纲一化公式:
μm=m2m1,μk=K2K1)μk,j=KjK1),f2=P2P1+P2)fi=PiP1+P2),ζ=C12m1K1,ω=ΩK1/m1,
μc,j=CjC1,Xi=xiK1P1+P2,b=BKP1+P2)bi=BiKjP1+P2,i=1,2;j=1,2,3),t=Tm1/K1
则式(3)变为
{μm,1X··1+2ζμc,1X1·+μk,1X1+2ζμc,2(X·1-X·2)+
μk,2(X1-X2)=f1sin(ωt+τ)
μm,2X··2+2ζμc,2(X·2-X·1)+μk,2(X2-X1)+
μk,3X2=f2sin(ωt+τ)
(4)
其矩阵形式为
[10
0μm][X··1
X··2]+[2ζ(1+μc)-2ζμc
-2ζμc2ζμc][X1·
X2·]+[1+μk,2-μk,2
-μk,2μk,2+μk,3][X1
X2]=[1-f2
f2]sin(ωt+τ)
3 非线性气膜动态特性参数的计算
3.1 气膜非线性刚度K2和阻尼C2的计算
应用PH线性法和变分法求解干气密封非线性雷诺方程,得到气膜角向涡动刚度的解析式[8]为
Ka′=4Riδ+E∫ξ01ζ2η(η1(ζ)cosω+η2(ζ)sinω)(1-ηcosω0)2dζ
(5)
稳态下Reynolds方程中,以复数来定义微扰动态压力的微扰量,其实部对应于气膜的刚度,虚部对应于气膜的阻尼。利用复数转换法以及多次的迭代平均法对稳态下气膜边值问题进行求解,获得了气膜轴向刚度和阻尼的近似解析解。
量纲一气膜轴向刚度、轴向阻尼[11]为
Ka=2∫ξ01ζη(η1(ζ)cosω+η2(ζ)sinω)(1-ηcosω0)2dζ
(6)
c=2∫ξ01ζ2η(η1(ζ)sinω+η2(ζ)cosω)(1-ηcosω0)2dζ
(7)
式中:
η1(ζ)=c10eβ1ζ+c′10e-β1ζ+(c11eβ1ζ+c′11e-β1ζ+
A12β1ζeβ1ζ-B12β1ζe-β1ζ)ε;
η2(ζ)=c20eβ1ζ+c′20e-β1ζ+(c21eβ1ζ+c′21e-β1ζ+
A22β1ζeβ1ζ-B22β1ζe-β1ζ-α2β1)ε;
c10=Aeβ1ζ/(e2β1ζ0-e2β1),c′10=-Aeβ1(ζ0+2)/(e2β1ζ0-e2β1),
c20=Beβ1ζ/(e2β1ζ0-e2β1),c′20=-Beβ1(ζ0+2)/(e2β1ζ0-e2β1),
c11=[-A1(ζ0e2β1ζ0-e2β1)+B1(ζ0-1)]/[2β1·(e2β1ζ0-e2β1)],
c′11=-A1e2β1/(2β1)+B1/(2β1)-c11e2β1,
c′21=-c21e2β1-A22β1e2β1+B22β1+α2β1eβ1,
c21=[-A22β1)ζeβ1ζ0-e2β1)+B22β1)ζ0-1)+
α2β1)eβ1ζ0-eβ1)]/[e2β1ζ0-e2β1],
A1=(-α1β1+α2)c20,B2=(α1β1+α2)c′20,
A2=(α1β1-α2)c10,B2=-(α1β1+α2)c′10,
A=1η)P0-1)(cosw0-η),B=1η)P0-1)sinw0,
n2+β20=β1,2β0=α1ε,nχ=α2ε,
ω=nφ+β0ζ,ω0=β0ζ,β0=ntanα,h=E/(E+d+x2)
气膜的轴向摆动刚度[7]:
K*=aπR2iPiδ
(8)
气膜阻尼:
C*=cRiPi2nr
(9)
将公式(5)—(9)运用Maple软件多次地拟合平均计算出密封气膜刚度K2和阻尼C2的非线性方程分别为
K2=-1 812.005 950α+2 463.115 574-
7.069 855 800×108x2α+9.609 540 480×108x2-
9.186 853 050×1013x22α+1.248 601 136×1014x22
(10)
C2=500.681 500 0α-684.420 115 5+1.986 379 500×108x2α-2.717 728 176×108x2+2.626 491 500×1013x22α-3.596 760 561×1013x22
(11)
气膜刚度随螺旋角和静环的振动位移的变化曲面,如图4所示,在静环振动位移方向上,气膜刚度的分布规律是先降低后升高。气膜阻尼随螺旋角和静环的振动位移的变化曲面,如图5所示,在静环振动位移方向上,气膜阻尼的分布规律是先升高后降低。

图4 气膜刚度随螺旋角和静环振动位移的变化曲面 图5 气膜阻尼随螺旋角和静环振动位移的变化曲面
3.2 实例计算
文中研究的样机的几何参数:内径Di=122 mm,外径Do=159 mm,平衡直径D=122 mm;螺旋槽数N=16,槽深2hg=8 μm,螺旋角α=77.92° ;硬环的外径为163 mm,内径为112 mm;静环的外径为165 mm,内径为122 mm。设计的运行参数:介质气体为氮气,介质压力为0.6 MPa,环境压力pi=0.101 3 MPa,转速n=16 500 r/min,气膜厚度h=3.47 μm。系统参数值如表1所示。

表1 系统的参数值
根据样机几何参数和表1所示系统参数,可得到:
m1=51.662 647 kg
μm=8.845 96×10-3
ζ=2.457 77
μk,3=K3/K1=1.457 7
μk,2=K2/K1=-0.660 352 022 6×10-5α+0.897 636 871×10-5-2.576 478 061x2α+3.502 019 125x2-
334 797.851 7x22α+455 029.568 5x22
(12)
μc=C2/C1=0.008 554 797 493α-0.011 694 211 77+
3 393.988 866x2α-4 643.593 619x2+0.448 770 383 9×109x22α-0.614 553 528 1×109x22
(13)
样机的螺旋角α=77.92° ,联立式(9)、(10),运用Runge-Kutta求解振动方程(1),获得该螺旋角下响应的时间历程图和相轨图,如图6所示,可知螺旋角α=77.92°时,单自由度下静环的最大振幅为4 μm。同样,联立式(11)、(12),运用Runge-Kutta求解振动方程(4),获得该螺旋角下响应的时间历程图和相轨图,如图7所示,可知α=77.92°时,双自由下静环的最大振幅为9 μm。即考虑了转子、轴承影响的干气密封系统静环的振动位移大于仅考虑干气密封的静环的振动位移。

图6 单自由度下螺旋角α=77.92°的时间历程图及相轨图

图7 双自由度下螺旋角α=77.92°的时间历程图及相轨图
3.2 螺旋槽螺旋角响应的优化
由文献[13]的螺旋角取值α=77.92°,在其邻域内取值,即螺旋角分别取76.78°、77.35°、78.50°、79.07°、79.64°,联立式(11)、(12),运用Runge-Kutta求解振动方程(4),获得不同螺旋角下响应的时间历程图和相轨图,如图8所示。可见,极小的螺旋角变化就可引起较大振动数值的变化。图9示出了螺旋角度与静环振动位移的关系。可见:静环振动位移随着螺旋角度(76.5°~80.0°)的增加先减小后增加;当α=78.50°时,振动数值最小,其最大振幅为7 μm,最大振速为25 μm/s。因此,当α=78.50°时,动环和静环的追随性最佳,证明该系统运行稳定。
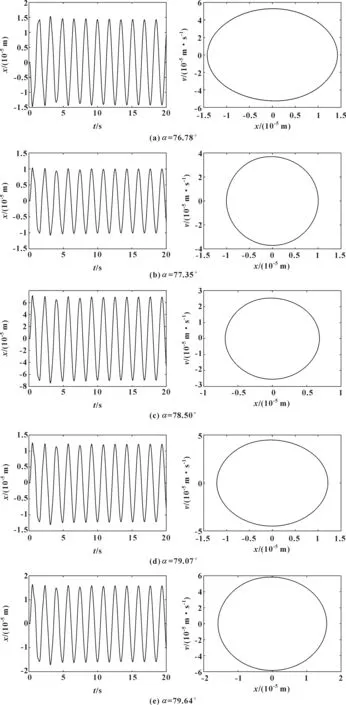
图8 双自由度下不同螺旋角的时间历程图及相轨图

图9 螺旋角度与静环位移的关系
Fig 9 The relationship between spiral angle and displacement
of static ring
3.3 螺旋槽槽深响应的优化
取螺旋角α=78.50°,以螺旋槽干气密封的槽深为控制变量,分别取槽深2hg=6,8,10 μm,利用Runge-Kutta求解振动方程(4),获得不同槽深响应的时间历程图和相轨图,如图10所示。可知:螺旋槽干气密封的槽深2hg=6 μm时,静环振动的最大幅值是7 μm;2hg=8 μm时,静环振动的最大幅值是6 μm;2hg=10 μm时,静环振动的最大幅值是5 μm。即,槽深数值越大,静环的振动幅值越小。
当E=3 μm时,通过Maple软件多次的拟合平均计算出气膜非线性刚度:
K2(E=3)=-20 384.759 80α+27 721.053 22-
5.553 574 030×109xα+7.551 913 295×109x-
8.033 919 000×1013x2α+1.091 345 691×1014x2
C2(E=3)=-56 432.556 00α+76 741.700 65-
1.495 387 605×1010xα+2.033 440 258×1010x+
6.349 430 000×1013x2α-8.674 215 395×1013x2
当E=4 μm时,螺旋槽干气密封气膜的刚度、阻尼:
K2(E=4)=-21 984.302 65α+29 895.989 48-
5.069 306 530×109xα+6.893 242 645×109x-
4.647 440 000×1012x2α+6.198 917 890×1012x2
C2(E=4)=-59 196.118 00α+80 498.853 70-
1.295 629 585×1010xα+1.761 748 975×1010x+
3.572 492 800×1014x2α-4.862 332 009×1014x2
当E=5 μm时,螺旋槽干气密封气膜的刚度、阻尼:
K2(E=5)=-23 315.892 80α+31 706.502 96-
4.632 838 905×109xα+6.299 588 900×109x+
4.122 853 500×1013x2α-5.618 742 845×1013x2
C2(E=5)=-62 300.699 60α+84 719.731 10-
1.136 956 435×1010xα+1.545 935 042×1010x+
5.062 677 000×1014x2α-6.888 841 635×1014x2
由图11可知,随着槽深的增加,静环振动位移是减小的。但是,从总的趋势来看,改变螺旋槽干气密封的槽深,静环振动的幅值没有发生太大的变化,而通过之前的改变螺旋槽的螺旋角度响应可以得出,螺旋角度的变化对干气密封系统静环的振动幅值影响比较明显。

图11 螺旋槽槽深与静环位移的关系
4 结论
(1)研究表明,静环在双自由度下的振动幅值比单自由度下的振动振幅值要大,所以研究干气密封系统考虑转子和轴承是非常必要的,文中所建立的双自由度转子-轴承-干气密封系统轴向振动模型更接近于实际工况。
(2)螺旋角变化对系统稳定性的影响较大,极小的螺旋角变化就可引起较大振动数值的变化;适当增大螺旋角度,可以提高整个大系统的稳定性。而螺旋槽槽深的改变,对干气密封静环的振动幅值几乎没有影响。
(3)由于转子-轴承-干气密封系统是一个复杂的非线性系统,其中的非线性动力学行为还有待实验验证。

