解析法及其应用*

☉内江师范学院数学与信息科学学院 熊 露

☉内江师范学院数学与信息科学学院 赵思林

解析法是解析几何思想方法的简称.解析法是指用代数方法来研究并解决几何问题的思想方法.解析几何兼具“数”的抽象和“形”的直观.解析法兼具思想性、方法性和工具性，也就是说，解析法既体现了数形结合的思想，又是研究几何曲线或曲面的基本方法，还为统一处理一些数学问题提供了基本工具［1］.本文主要探究了解析法在函数、三角、向量、不等式和平面几何等领域中的应用.

一、在函数中的应用

例1对于x∈R，求函数的值域.

分析：若用代数方法则较难下手，但注意到两个根式就可以发现，f（x）实质上是两个距离之差的形式，由此可以构造距离来简化问题.

解：易知从而问题转化为求点C（x，2）到点A（-3，0）与点B（2，0）的距离之差，如图1所示.因此f（x）=|CA|-|CB|.

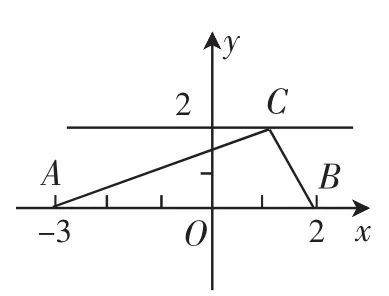
图1

因为点C（x，2）是定直线y=2上的一个动点，

所以在△CAB中，||CA|-|CB||＜|AB|，

即-5＜|CA|-|CB|＜5.

故f（x）的值域为（-5，5）.

例1的推广：若a＞0，Δ1=b12-4ac1≤0，Δ2=b22-4ac2≤0，求函数的值域问题都可以用上述方法来解决.

例2若x、y∈R且满足|x|+|y|=3，试求m=x2+y2-2x-2y的取值范围.

分析：由于|x|+|y|=3，m=x2+y2-2x-2y，很容易想到用数形结合的思想，将问题转化为在|x|+|y|=3的条件下，求圆的半径的最值问题.

解：|x|+|y|=3表示正方形ABCD，m=x2+y2-2x-2y可整理为（x-1）2+（y-1）2=m+2.该方程表示以M（1，1）为圆心，为半径的圆，如图2所示.

所以只需求正方形ABCD边界与圆族中的公共点的最小（或最大）圆的半径，即当⊙M与正方形ABCD的边AD相切时，圆的半径最小，即当且仅当

当⊙M过点B（-3，0）或C（0，-3）时，圆的半径最大，

即当且仅当x=-3，y=0或x=0，y=-3时，mmax=15.

二、在三角中的应用

例3已知求β的值.

分析：首先对方程进行整理，用代数方法无法直接对方程进行求解，但经仔细分析可以发现通过构造直线和圆，利用圆心到直线的距离与圆的半径之间的关系，能够使问题得以解决.

解：由题意，得（sinβ+cosβ）cosα+（1-sinβ+cosβ）sinα-

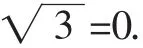
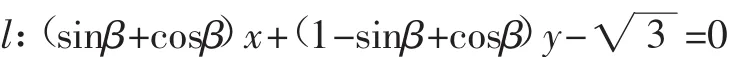
构造直线和圆O：x2+y2=1.

显然点（cosα，sinα）既在直线l上，又在圆O上，所以圆心（0，0）到直线l的距离不超过圆O的半径，即有

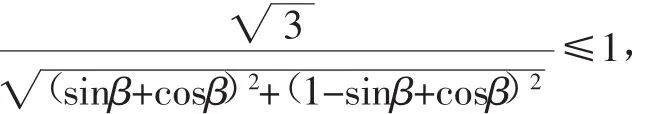
从而得到，cosβ≥sinβ.

因为

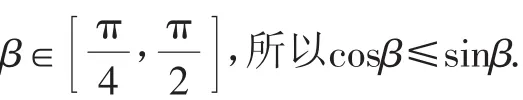
故

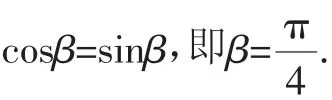
三、在向量中的应用

在解决一些与向量有关的问题时，应适当考虑解析法，这样能够使数与形紧密地结合起来，解决问题也会更加方便.

例4在△ABC中，AB=BC=CA=2，设点D、E满足求t的值.（本题为2012年高考数学天津卷理科第7题的改编）

解：以BC边和BC边的中垂线所在的直线为坐标轴，建立平面直角坐标系，如图3.

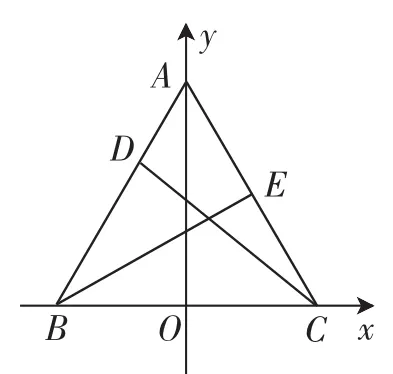
图3

例5在平面上，求的取值范围.（本题为2013年高考数学重庆卷理科第10题的改编）

解：由题意，以A为坐标原点，直线AB1、AB2分别为x、y轴建立平面直角坐标系.

四、在不等式中的应用

例6已知x、b、c∈R且b2+4c2=1，求证：|b-2cx|≤

分析：一般我们习惯将x视为变量，把b、c视为常量，但这样做不方便运用b2+4c2=1的几何意义.若将x视为常量，b、c视为变量，再令2c=e，则有b2+e2=1是一个单位圆，这样自然就可以用解析法了.

证明：不妨设x为常量，令2c=e，则b2+e2=1.

在b=xe中，若把x视为常量，b、e分别视为纵坐标和横坐标，则方程b=xe表示直线，b2+e2=1表示单位圆.从而圆上的任意一点（e，b）到直线xe-b=0的距离不大于此圆的半径，即

注：此题也可用柯西不等式求解.

例7若x、y、z∈R且满足其中m＞0，求证

分析：若把方程组中的z看作常数，则方程组就可以看成是一个二元二次方程组.但第二个方程是一个椭圆，令2y=y1，就可以把第二个方程变成一个圆.

证明：记2y=y1，则方程组的几何意义是直线x+y1=m+3z与圆有公共点，所以圆心（0，0）到直线的距离小于或等于圆的半径，即有

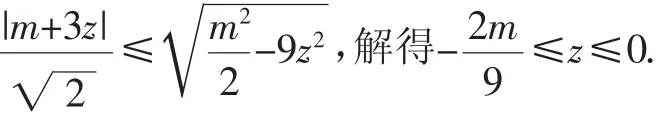
同理可证

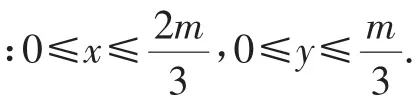
五、在平面几何中的应用

例8证明三角形的三条高线相交于一点.

证明［2］：以△ABC的边AB及其高线分别为x轴和y轴，建立平面直角坐标系，如图4.

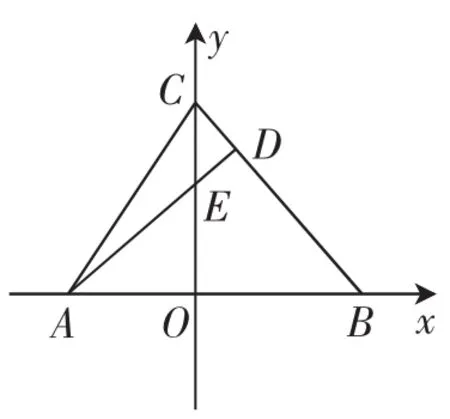
图4

在平面直角坐标系中，设A，B，C的坐标分别（a，0），（b，0），（0，c），过A作BC边的高线AD交OC于点E.由平面几何知识可得从而，所以AD所在直线方程为，即bx-cy-ab=0.故E点的坐标为

同理可得△ABC中AC边上的高与y轴相交的点的坐标为所以点是三条高线的交点坐标.

故三角形的三条高线相交于一点.

推广：在平面直角坐标系中，已知三点的坐标为Ai（xi，yi）（i=1，2，3），则三点间的线段所围成的图形的面积为其中特别地，D=0时当且仅当

A1、A2、A3三点共线，可用于解析几何中证明三点共线问题.

例9如图5，自圆O外一定点M，向圆引切线MA、MB，A、B为切点，过点M的任一直线交定圆于C、D，交AB于E.

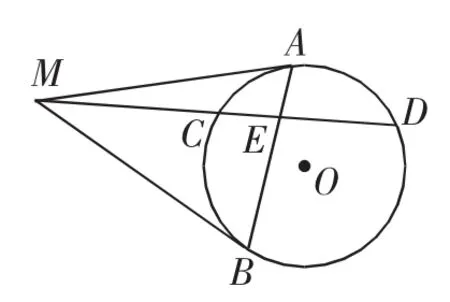
图5

证明：设圆的方程为

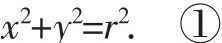
设点M的坐标为（x0，y0），

则AB的方程为

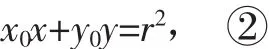
设割线MD所在直线的参数方程为

将③代入①得（x0+tcosα）2+（y0+tsinα）2=r2，

即

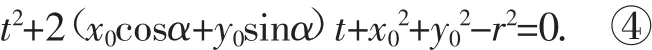
设方程④的两根为t1，t2，则由根与系数的关系可得

由参数t的几何意义知：

因此方程的根t满足

又由几何意义可知：

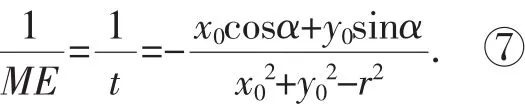
因此由⑤⑦可知

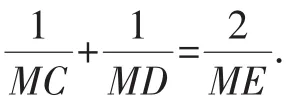
评注：本题若采用纯平面几何法来证，则有较大难度.

对于与圆有关的结论，往往会联想到椭圆.

推广1：自椭圆外一定点M，向椭圆引切线MA、MB，A、B为切点，过点M的任一直线交定椭圆于C、D，交AB于E.求证：

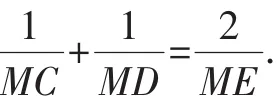
证明：从略.

推广2：如图6，自二次曲线C外一定点M，向曲线引切线MS、MT，S、T为切点，过点M的任一直线交定曲线于P、Q，交ST于R.求证：

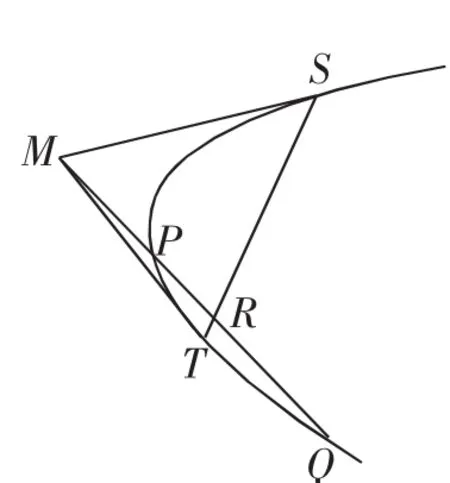
图6

证明：从略.

评注：利用传统的几何法来解决平面几何问题，往往需要添加辅助线［2］，并且对解题技巧也有较高的要求，而解析法具有思路清晰、目标明确、多算少想等特点，故利用解析法来解决平面几何问题，对培养数学运算素养大有裨益.