考题研究：答题分析·导向之思·教学设计——以海安市八上期末卷把关题为例

☉江苏省海安市海陵中学 魏爱凤

一道精彩的试题，不仅通俗易懂，关键是各层次的学生都能动得了手，而且都能有所收获；不仅本年级的学生能够解决，甚至高年级的学生看到题目也觉得题目有趣；不仅能考查学生的基础知识，而且通过试题能充分考查出学生的水平和潜力.本地区八年级上学期期末试卷的一道把关题就具有上述特点.本文先呈现这道考题并概述学生的答题情况，再跟进教学思考，抛砖引玉，供研讨.

一、考题及学生解答情况概述

考题：已知x+=k，k为正实数.

（1）当k=3时，求x2+的值.

（3）小安设计一个填空题并给出答案，但被老师打了两个“×”！如图1.

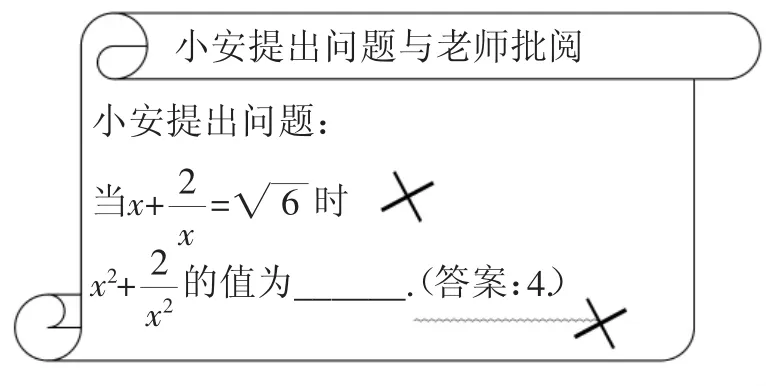
图1

小安没看懂老师为什么指出两个错误.如果你看懂了，请向小安解释一下！

学生解答情况概述：

解法1：从已知条件推出矛盾.

解法2：求出x+的取值范围，运用“公式a+b≥2”（.高中学习的基本不等式）

该方法需要学生有一定的建模能力，要求较高，部分教师补充过上述公式，少数学生能使用该方法，该方法的解释是简洁有力的.

解法3：解方程得方程无解.

少数会解一元二次方程的学生会用该方法.

解法4：解出“虚根”.

如图2，学生解法截图如下：

图2

只有一个学生有这样的解法，可能该学生在校外机构参加竞赛辅导时有教师提前培训过这类知识.

二、考题的教学导向之思

1.考题引导钻研教材

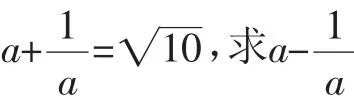
这道习题与整式乘除一章所学的配方变形密切相关，它们的对应关系如图3所示：

图3

可见这道考题引导教师回归教材，但又倡导从简单的“教教材”走向“用教材教”，即不只满足于对教材习题的简单教学，而且要关注教材前后不同章节，关联融通，促进学生深刻理解相关知识，做到举一反三，做一题，会一类.

2.考题引领“化错教学”

本题是一道完全平方公式、分式、二次根式的综合题，考查学生的代数运算推理能力和对所学知识灵活运用的能力，特别是对学生纠错与究错能力的培养，对学生的数学素养提出了全新的要求，真正提高学生的数学能力.这里可特别提及小学数学特级教师华应龙老师近年来倡导的“化错教学”，即课堂教学中不但要重视纠错与究错教学，更重要的是善于在课堂教学中“诱错”“捉错”，并把这些错漏的“生成性资源”融入后续教学进程，引导更多学生参与究错、评析，训练学生倾听、思辨与善于优化的素养.

3.考题倡导“开放教学”

不少教师看到第（3）问后，想起一个经典问题“面积一定的矩形中，正方形的周长最小”，误认为只有少数优生能够解决，后来通过阅卷发现这种担心是多余的，学生的解法有很多，既有适合全体学生的普通解法，也有较难的解法，甚至有学生用初三和高中的知识来解决.这充分体现了不同学生对题目的理解深度的不同，学生的很多解法也值得教师好好学习.这里可特别提及南京大学哲学系郑毓信教授倡导的“开放的数学教学”，即教学过程中要通过运用开放题促进“开放的数学教学”.这道考题第（3）问的呈现方式就是引领“开放式教学”的最好方式，即问题的答案可以不是唯一的，但需要关注学生不同解法背后的依据、道理，让不同学生上台展示、讲演他们的解法，引导其余学生倾听并评析不同解法，并学会批判性接受，优选好的解法融入自己的知识体系.

三、考题的教学微设计

知易行难，以下本着教学研讨的兴趣，给出上文考题的讲评教学微设计.

问题1：已知一个非零实数x，请用含x的式子表示它与它的倒数之和.

预设：x+.

追问1：若x为正数，你会分析式子x+的最小值吗？

追问2：若x为负数，你会分析式子x+的最大值吗？

预设：学生可以先猜想出最值，然后设法证明，初二学生可以用配方法解决.

问题2：已知x+=k，k为正实数.

（1）当k=3时，求x2+的值；的问题，则投影到黑板上，引导学生参与辨析这个问题是否错误，并安排全班讨论，最后各组汇报不同的方法，教师跟进评析.如果有学生的思路类似高中学习的基本不等式，也可给出“公式a+b≥2 Ｅ ”，并运用配方法进行推理证明.

四、写在后面

教学即研究.一次考试之后得到的不只是冰冷的分数，也不只是区分了不同学生，其实还有很多值得我们去关注和研究，如挑选一些“好的题目”深入分析学生答题情况，解读并思考试题对我们教学有怎样的导向作用，并构思如何开展讲评教学，或者由一道题如何训练一类问题，提升解题教学效果，还可以由一道题出发，思考该题与后续哪些知识点关联、呼应，也就是求深、想透、学活的追求.