指向教学的中考试题研究*——以2018年南通市部分中考试题为例

☉江苏省如皋市石庄镇初级中学 印冬建

中考试题研究是一项日常的教学工作.在中考结束后，很多老师立即投入到新的中考题的研究中去，他们热衷于对新颖考题、压轴考题解法的研究，而对考题教学价值的研究不够深入.笔者认为，这样的试题研究是不全面、不科学的.中考具有极强的导向作用，它是我们进行数学教学的重要依据.日常教学中，“四基”的教与学该到什么程度，学生发展的底在哪里，每一年的中考试题都有明示，都需要我们这些一线教师从试题中挖掘出来，并在教学中加以落实.近期，笔者结合南通市2018年中考卷进行了部分考题的教学价值分析，明晰了教学的方向，现将其呈现，供大家参考.

一、抓住核心知识，培养应用意识

核心知识是学段中最重要的数学知识，它们具有较强的应用性和发展性，在解决问题和后续学习中能发挥出巨大的作用.因而，对核心知识的考查也就成为了中考的重点.综观2018年各地的中考卷，需要用到方程、勾股定理、全等三角形的判定和性质、函数的图像及性质等为代表的核心知识的考题屡见不鲜.中考试题的研究，理所应当该透过试题找核心，从考题中发现我们“司空见惯”的那些数学知识中真正的“核心”，给它们以准确的教学定位，力求通过日常教学的强化，使学生逐步形成自觉应用的意识.

题1：（原卷第24题）如图1，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D，且交⊙O于点E.连接OC、BE，相交于点F.

（1）求证：EF=BF；

（2）若DC=4，DE=2，求直径AB的长.

考题简析：本题是一道以圆为背景的综合题，主要考查切线的性质、垂径定理、矩形的判定与性质、勾股定理等知识.解答第（1）问可根据平行线的性质、垂径定理逐步证得；解答第（2）问应先证明四边形EFCD是矩形，然后由勾股定理建构出含有半径r的方程r2=（r-2）2+42，进而求出直径AB的长是10.显然，第（2）问的解答需要用到勾股定理、方程、矩形的性质与判定等学段核心知识.

教学启示：与一般数学知识相比，核心知识具有较强的应用性和发展性，在中考中有很多的应用，因而它们理应走向数学教学的“前台”.在上面的分析中，之所以说勾股定理、方程等是学段核心知识，是因为在2018年南通卷中对这些知识的考查还有多处.先来说说说对勾股定理的考查，第27题至少三处需要用到勾股定理求解，其中有一处和题1一样需要将勾股定理和方程链接在一起解题，第22题需要将勾股定理与三角函数结合起来解决实际问题.至于方程，全卷考查的“点”不下十处，如第20题的解方程，第25题的列方程解决实际问题，第18题的列方程解决几何问题等.如此多的考查点分布，充分体现了勾股定理与方程的重要地位，一线教师务必高度重视.关于勾股定理，记得科学家曾试图用它与外星人沟通，足见勾股定理在数学界的地位.从南通卷对勾股定理的多次同卷考查可见，初中学段的勾股定理教学绝不能仅仅停留在知其然的地步，我们应努力在学生知其所以然的基础上，让他们经历更多的勾股定理与相关核心知识链接与融合的过程，使他们在分析问题和解决问题的过程中能将勾股定理作为一个重要的工具自觉提取出来并加以应用.方程的重要性，笔者不再赘述了.通过2018年南通卷的分析发现，仅仅会解方程是不够的.初中阶段，学生学习了一元一次方程、一元二次方程、二元一次方程（组）、分式方程等多种形式的方程，对这些方程的学习都是按照“定义—解法—应用”的流程展开的，而且应用主要侧重于实际问题中的列方程与解方程.事实上，方程作为解题模型应用的范围是很广的.在教学中，我们应创设更为丰富的数学情境或生活情境，让学生反复经历“抽象数学问题—建构方程模型—解模检验—解决问题”的过程，从而让学生体会到方程模型的价值所在，不断提高用方程解决实际问题和数学问题的能力.

二、渗透数学思想，发展数学思维

数学思想是初中数学教学的重要内容.为了凸显数学思想的价值，发挥中考的导向作用，在各地的中考卷中，都会设计一些指向抽象、分类、类比、模型、数形结合等数学思想的考题.面对这些考题，我们不仅要考虑数学基础知识的价值，还应从思想方法的角度挖掘考题的价值，从发展学生理性思维的高度明晰数学思想的教学方向.这种扎根于中考试题的深度研究，将有助于我们真正理解数学思想的价值，从而在教学过程中把握教学契机，渗透数学思想，让学生在思想感悟与应用中不断发展数学思维，养成“言之有理，述之有据，反思质疑”的良好习惯.

题2：（原卷第26题）在平面直角坐标系xOy中，已知抛物线y=x2-2（k-1）x+k2-k（k为常数）.

（1）若抛物线经过点（1，k2），求k的值；

（2）若抛物线经过点（2k，y1）和（2，y2），且y1＞y2，求k的取值范围；

（3）若将抛物线向右平移1个单位长度得到新抛物线，当1≤x≤2时，新抛物线对应的函数有最小值-，求k的值.

教学启示：理性思维是一种较常见的思维方式，是建立在证据和逻辑推理法则之上的思维方式.可见，以理性思维为主的数学思维应遵循逻辑性，追求严密性，它有着明确的方向，需要充分的依据.上面的题2，就是一道能很好地考查学生数学思维的考题.结合考题分析不难发现，如果没有理性思维的高度参与，在本题的解答过程中遗漏情形或误增结果都是极有可能出现的.因而，在数学教学中，务必重视发展学生的数学思维.而随着对中考试题的深入分析，我们还发现当大量数学思维参与解题时，一定会有许多数学思想蕴含其中.上面的题2自不必说，在对第（3）问中k的取值的探索过程中，需要分类讨论，需要数形结合，还需要数学模型，几种常见数学思想的作用都得到了极致发挥，而且只有将这些数学思想的价值真正发挥出来，我们才有可能正确地给出本题的求解过程.我们再来看试卷中的一道填空题：（原卷第13题）一个等腰三角形的两边长分别为4cm和9cm，则它的周长为______cm.本题考查的是等腰三角形的性质和三角形的三边关系.给出的条件“等腰三角形两边的长为4cm和9cm”，并没有明确底边和腰，因此要分两种情况讨论：①当腰是4cm、底边是9cm时，不满足三角形的三边关系，因此舍去；②当底边是4cm、腰长是9cm时，能构成三角形，则其周长=4+9+9=22（cm）.这道题同样需要分类讨论参与，而且仅仅分类讨论还不行，最后还必须对所得结果能否满足三角形三边关系进行检验，这就需要数学思维的高度参与.所以，在数学教学中，我们应该注意到数学思维往往与数学思想“伴生共长”这一特性，将发展学生的数学思维与数学思想教学结合在一起，有效融入教学进程中.在新知探索与问题解决过程中，要注意引导学生梳理其涉及的数学思想，并体会思维过程中不同数学思想的价值，从而养成坚持真理、修正错误、反思质疑的意识和习惯.

三、注重实践体验，提高数学能力

《义务教育数学课程标准（2011年版）》（下称《课标（2011版）》）提出“通过义务教育阶段的数学学习……使学生增强发现和提出问题的能力，分析和解决问题的能力”（下称“四能”）.显然，解答中考题不只需要知识，还需要一定的数学能力作为支撑.因而，只有我们在中考试题研究中厘清了解题的能力需求，才可能在接下来的教学中有的放矢地培养学生的数学能力.在2018年南通中考卷中，就存在着一些能力要求高于知识要求的考题，这些考题对一些具体的能力，如阅读、作图、运算、数据整理、建构模型等显性数学能力提出了较高的要求.而这些数学能力的养成，无一不与学生的自主实践有着很大关联.因而，日常教学中，我们就应围绕中考解题所需要的数学能力设计一些能引导学生自主实践的数学活动，让他们在体验中逐步形成个性化的数学能力.

题3：（原卷第18题）在平面直角坐标系xOy中，已知A（2t，0）、B（0，-2t）、C（2t，4t）三点，其中t＞0，函数y=的图像分别与线段BC、AC交于点P、Q.若S△PAB-S△PQB=t，则t的值为______.

教学启示：在数学教学中，教师对数学知识与技能一直都是十分重视的，在《课标（2011版）》引入了数学思想和数学基本活动经验后，“四基”才真正进入了一线教师的视野.要注意的是，虽然“四能”与“四基”同时出现在《课标（2011版）》中，但没能引起一线教师的足够重视.通过对2018年南通卷的分析，笔者发现命题人给出了多道考查阅读、作图、数据整理等数学能力的考题，这无疑给我们的教学敲响了警钟.数学教学不仅要重视“四基”，还应重视“四能”.我们应根据学生能力发展的进程合理设置有梯度的数学活动，让学生在自主实践体验中，不断提升数学能力.比如，为了培养学生的数学阅读能力，我们可以从文本、图形、符号等多个维度设计单独或混合多种素材的阅读材料，引导学生开展自主阅读并提供相应的指导与帮助，从而提高他们的数学阅读能力；而作图能力的提升离不开作图过程的自主历练，我们要在学生掌握基本作图的情况下，引导他们进一步探索复杂图形的规范作法，明晰其中的原理，并通过反复应用，使这些作图的方法与原理逐步固化为学生的作图能力……

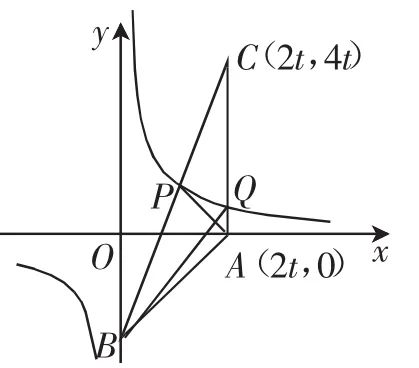
图2

四、弘扬数学文化，涵养家国情怀

不管哪一门学科，都需要坚持正确的育人方向，数学也不例外.中考是具有明显导向性的考试，一线教师应坚持的正确育人方向将会很好地体现在这场综合性测试中.因而，在研究数学中考题时，除了关注考题涉及的“四基”和“四能”，我们还应关注考题所蕴含的育人力量，努力挖掘并放大考题中的正能量.2018年的中考卷，试题情境十分丰富，除了常见的数学情境，还从我国古代数学家的研究成果和我国改革开放四十年辉煌成就中选取了很多典型素材作为考题背景.这些基于国家背景和时代背景的考题，意在让考生和一线教师知道国家历史之悠久，国家实力之强大，国家发展之快速……很好地传递中考命题人的家国情怀，这给一线教师带来的启示莫过于：在日常教学中注意弘扬祖国的优秀数学文化，涵养学生的家国情怀.

题4：（原卷第15题）古代名著《算学启蒙》中有一题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之.意思是：跑得快的马每天走240里，跑得慢的马每天走150里.慢马先走12天，快马几天可追上慢马？若设快马x天可追上慢马，则由题意，可列方程为______.

考题简析：本题是一道关于一元一次方程的名题，素材取自于我国元代数学家朱世杰的著作《算学启蒙》.题中不仅给出了著作中的原题，还将其转译成现代文.这样的命题设计，很好地体现了命题人的学生视角和数学视角：一方面，两种文本的对照呈现，有效规避了文言文单一陈述可能带来的阅读偏差，减少“非数学错误”出现的机会；另一方面，两种文本的对比，能让学生很好地体会我国古代数学家取得的辉煌成就，初步感知这一成就在世界数学史中的领先地位，增强民族自豪感.解答本题，读懂现代文陈述的数学问题并抽象数量关系是关键.根据已有的知识和经验，抓住题中给出的“快马追上慢马”这一结果，可以抽象出“快马走的路程=慢马12天走的路程+慢马12天后走的路程”的数量关系，从而列出方程240x=12×150+150x.

教学启示：鲁迅先生说：只有民族的，才是世界的.几千年来，中华民族取得了丰硕的数学成就，为世界数学的发展作出了巨大贡献.这些成就理应成为数学教师最重要的教学素材，在日常教学活动中合理呈现并有效应用.数学教学，育人为先.章建跃教授说数学教学要“发挥数学内在的育人力量，谋求学生的长远发展”，我想，弘扬祖国优秀的传统数学文化应该是有效的途径之一吧.无论是过去、现在还是将来，一线教师都应将国家成就与学生好好分享，随时随地有意识地激发学生对祖国的热爱.如教学2018年南通卷第4题时，不仅要让学生弄懂“如何用科学记数法表示827 000”，更要让学生从“数字之大”上感知到“2017年国内生产总值达到827 000亿元，稳居世界第二”这一巨大发展成就及其获得之不易.我想，只有如笔者所述这样，将知识教学与情感育人融为一体，数学内在的育人力量才能真正得以发挥出来，从而在弘扬祖国优秀数学文化的同时，涵养学生的家国情怀.

研究中考试题，几乎每一位初中数学教师都会做.紧盯新颖题和压轴题，深度探索解题方法，本无可厚非，但如果只关注对这些考题解法的探索，而无视其教学价值分析，笔者认为这是十分不妥的.中考试题的价值是多维的，但指向教学无疑是最重要的.因而，我们研究中考题，更应站在教学的角度分析考题：摸清考查的核心知识，在渐进训练中发展学生的应用意识；关注涉及的数学思想，在反复感悟中锻炼学生的数学思维；理解试题的探索历程，在实践操作中提高学生的数学能力；把握考题的文化脉络，在浸润体验中涵养学生的家国情怀……一年一度的中考又要来了，一大批“新鲜”的中考试题又将“迎面走来”，但愿本文所陈述的观点与做法能给大家一些启示.