一题多解“再归一”，教学设计“重变式”——以F市一道九年级圆的综合题研习为例

☉江苏省江阴实验中学 薛春燕

各地期末试题出来之后，一些网站、QQ群里都会第一时间转发一些精品试卷，特别是对试卷中一些原创“把关题”（位于试卷中最后位置的较难题）进行求解、研习，笔者恰在某群里，发现大家对F市九年级试卷中一道与圆有关的综合题的解法进行了探究，说法不一，有些认为试题设计巧妙，铺垫恰当，也有教师认为从其他路径运算繁杂，不是好题.本文就先引出这道考题，再跟进反思并给出教学设计，供研讨.

一、考题及思路突破

考题：（2019年1月F市九上期末卷）如图1，AB、AC是⊙O的弦，过点C作CE⊥AB于点D，交⊙O于点E，过点B作BF⊥AC于点F，交CE于点G，连接BE.

（1）求证：BE=BG；

图1

（2）过点B作BH⊥AB交⊙O于点H，若BE的长等于半径，BH=4，AC=2，求CE（的长.

思路突破：（1）由同弧所对圆周角相等，可得∠BAC=∠BEC.结合垂直的条件，可得∠BFA=∠BDG=∠BDE=90°.∠ABF=∠ABE，于是∠BGD=∠BEC（等角的余角相等），从而BE=BG.

图2

（2）如图2，连接OB、OE、AE、CH.由四边形ABHC内接于⊙O，可得对角互补，即∠ACH+∠ABH=180°，于是∠ACH=90°=∠AFB，从而可 得 BF∥CH.由 BH⊥AB，得∠ABH=90°=∠BDE，则BH∥CD.于是可确认四边形BGCH是平行四边形，则CG=BH=4.由BE=OB=OE，得△OBE是等边三角形，则∠BOE=60°.所以∠BAE=∠BOE=30°. 在Rt△ADE中，DE=AE.设DE=x，则AE=2x.由（1）得BE=BG，结合AB⊥CD，则DG=DE=x，CD=x+4. 在Rt△ADE中，AD=x. 在Rt△ADC中，AD2+CD2=AC2，即（x）2+（x+4）2=（2）2，解得x1=1，x2=-3＜0（舍去），所以DG=1，CE=CG+GD+DE=6.

回顾反思：这道考题真正的难点在第（2）问，线段相对较多，找准突破的解题方向或目标图形是关键.上面的解法，解题思路是先发现四边形BGCH是平行四边形，瞄准Rt△ADC，从而构造方程，成功求解.上述解法运算量不大.以下再给出一种思路，运算量偏大，但有利于我们看清这道问题的基本结构.

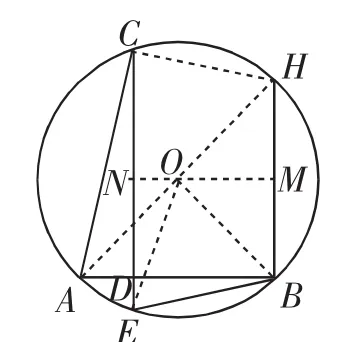
图3

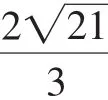
上述解法在图3中理解起来显得较为繁杂，事实上可以删减无关线条，适当简化为以下问题：

这样以上求解就可发挥作用了.

图4

命题商榷：从这道考题的不同解法来看，找准原考题的思路，运算量不大，但是如果走向了其他方向，则运算繁杂，且数据不太“友好”，容易中途放弃繁杂数据，值得命题者慎重打磨这类问题.

二、以考题为例的解题教学设计

三、进一步的思考

例题呈现：题略，见上文“考题”.

教学组织：学生独立思考5分钟后，应该可以安排学生交流解法或思路进展.半数学生应该能解决第（1）问，但第（2）问很难在这么短的时间内贯通思路.这时可“访谈”优秀学生：你们有哪些思路方向，或进展如何？并预设如下一些铺垫式问题：

铺垫问题1：由条件“BE的长等于半径”能解读出哪些信息？（预设：连接OB、OE，可得△BOE是等边三角形，所对圆周角都是30°等，再如连接CH、AH后，可得△ACH是含30°角的特殊直角三角形，等等）

铺垫问题2：由条件“BH⊥AB”能解读出哪些信息？（预设：连接AH，可确认AH为圆的直径，连接CH后，可由直径所对圆周角为直角，知∠ACH为直角）

铺垫问题3：四边形BHCG的形状有什么特殊之处吗？（预设：是平行四边形）

铺垫问题4：连接AE，得到的直角三角形ADE有什么特殊之处吗？（预设：该直角三角形是含30°的特殊直角三角形）

例题变式：如图5所示是有公共顶点C的两个等边三角形ABC、CDE，连接AE、BD，得到四边形ABDE.

（1）判断四边形AEBD的对边AE与BD的位置关系，并说明理由；

预设：AE∥BD.如图6，过点C作CG⊥AE，垂足为G，交BD于H点.在△ACE中，先由“三线合一”证出∠ACG=∠ECG，进一步导角，得∠BCH=∠DCH，从而由“三线合一”可证得CH也是BD边上的高，于是AE∥BD.

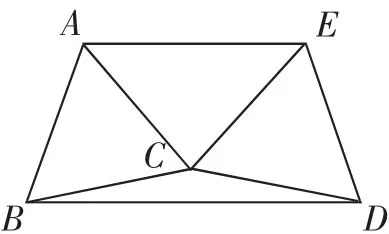
图5

图6

预设：由特殊数据可得∠ACE=120°，从而有∠BCD=120°，从而确认BD=.

预设：由特殊数据可得∠ACE=90°，从而有∠CBD=15°，于是把目光聚焦在直角三角形BCH中，构造图形可得BH的长，进一步求出BD的长.

预设：聪明的学生应该发现，这组数据使得运算很繁杂，但正是考题第（2）问的“问题结构”.

1.教师解题要从一题多解走向多解归一

教师解题需要思考思路的自然、合理，能否回到定义去解题，同时要尝试从不同角度去攻克、贯通解题思路，也就是先要追求一题多解，而不是单一路径、狭窄通道贯通思路.对于几何题，特别要注意一题多解的解题追求.在一题多解的基础上，还要思考不同解法“殊途何以同归”，想清不同解法之间的联系，条件之间的相通、等价等联系和对应，这样就达到了对问题本身的深刻理解，为后续解题教学提供了必要的备课保障.在上课、听课过程中，有时会发现教师对有些学生的解法难以理解，或简单干预、打断、忽略处理，说到底，都是课前教师本人对问题的“一题多解”做得还不够.

2.回顾反思要揭示问题结构和呈现顺序

解题研究一个重要环节是回顾反思.在这个阶段，要重视揭示问题的深层结构，并思考问题条件呈现的“序”.具体来说，上文考题第（2）问的深层结构就是后面我们在解题教学设计中提供的“例题变式”.而条件呈现的“序”也是非常重要的，有助于我们重新认识问题中的众多条件是如何渐次出现的，很多情况下，解题经验与教学经验表明，若画出的几何图形严重不准，都是因为对条件呈现的“序”辨识不清、理解不深，如果想清条件、线段是怎样一步步渐次呈现的，则图形往往会比较精准.

3.解题教学注重为学生预设铺垫式问题

解题教学时就题讲题往往“入宝山而空返”，回顾反思之后，能提供一些问题的深层结构，再小结一些解题策略或模型积累，往往能帮助优秀学生提高“模式识别”能力.但要帮助更多学生真正理解问题，以便达到“解一题、会一类”的效果，还是需要我们精心备课，深入构思，预设出系列铺垫式问题，从而帮助更多学生弄懂、弄深、弄透问题，并在铺垫式问题的引领之下，获得解题自信.想来，这也是所谓“春风化雨、润物细声”的高品质教学之追求吧.