基于樽海鞘群算法的图像匹配方法*
王 斐,贾晓洪,李丽娟,王忠勇
(1 中国空空导弹研究院,河南洛阳 471009;2 郑州大学信息工程学院,郑州 450001)
0 引言
图像匹配是指利用已知目标图像在另一幅图像中搜寻相似目标区域的过程,又称模板匹配,已经成功应用于多个领域[1-2]。
传统的图像匹配算法利用遍历式搜索策略,匹配点对多,匹配效率低。近年来,研究者将群智能优化算法引入图像匹配,大大减少了图像匹配块的数量和计算量[3-4]。群智能优化算法是一种基于群体行为的方法,通过个体间的协同合作实现全局搜索,有效解决了大多数全局优化问题,提高了匹配效果。文献[5]利用蚁群算法对像素进行聚类,设置了初始聚类中心,将蚂蚁与聚类中心的相似度作为引导函数,实现了快速匹配。文献[6]针对传统粒子群优化(PSO)算法局部收敛能力不强,易出现早熟收敛现象问题,改进了速度更新公式,获得了较好的匹配精度。
传统群智能优化算法及其改进算法,虽然可以获得较好的匹配效果,但这些算法均存在参数较多,调节复杂,匹配精度和匹配效率有待提高的问题。樽海鞘群算法(salp swarm algorithm,SSA) 模拟了樽海鞘链的群体行为,是一种较新颖的群智能优化算法。每次迭代中,领导者指导追随者,以一种链式行为,向食物移动。移动过程中,领导者进行全局探索,而追随者则充分进行局部探索,大大减少了陷入局部最优的情况。SSA的控制参数较少且易于调节,避免了因参数调节复杂而使匹配失败。
文中将SSA算法引入图像匹配,将匹配问题看作组合优化问题,通过对参数调节、匹配精度、匹配效率等进行分析,证明算法在图像匹配中的有效性和优越性。
1 SSA算法
1.1 算法描述
樽海鞘是一种海洋无脊椎动物,身体呈桶状且几乎完全透明,以水中浮游植物为食,通过吸入和喷出海水完成在水中移动。在深海中,樽海鞘以一种链式的群行为进行移动和觅食,这种“奇特”的群行为引起了研究者的兴趣。
樽海鞘的链式群行为,通常个体首尾相接,形成一条“链”,依次跟随进行移动。在樽海鞘链中,分为领导者和追随者,领导者朝着食物移动并且指导着紧随其后的追随者的移动,追随者的移动按照严格的“等级”制度,只受前一个樽海鞘影响。这样的运动模式使樽海鞘链有很强的全局探索和局部开发能力。
Seyedali等人于2017年建立了基于樽海鞘链的数学模型,提出了用SSA来解决一系列优化问题[7]。
1.2 种群初始化
设搜索空间为D×N的欧氏空间,D为空间维数,N为种群数量。空间中樽海鞘的位置用Xn=[Xn1,Xn2,Xn3,…,XnD]T表示,食物的位置用Fn=[Fn1,Fn2,Fn3,…,FnD]T表示,n=1,2,3,…,N。搜索空间的上界为ub=[ub1,ub2,ub3,…,ubj,…,ubD],下界为lb=[lb1,lb2,lb3,…,lbj,…,lbD],j=1,2,3,…,N。
XD×N=rand(D,N)·(ub-lb)+lb
(1)
1.3 领导者位置更新
在樽海鞘链移动和觅食过程中,领导者的位置更新表示为:
(2)

式(2)表明,领导者的位置更新仅与食物的位置有关。c1是优化算法中的收敛因子,起到平衡全局探索和局部开发的作用,是SSA中最重要的控制参数。c1的表达式为:
(3)
式中:l是当前迭代次数;L是最大迭代次数。收敛因子是一个2~0的递减函数。
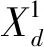
1.4 追随者位置更新
在樽海鞘链移动和觅食的过程中,追随者通过前后个体间的彼此影响,呈链状依次前进。它们的位移符合牛顿运动定律,追随者的运动位移为:
(4)
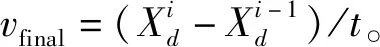
考虑到在优化算法中,t是迭代的,设迭代过程中t=1,并且v0=0。那么式(4)可以表示为:
(5)

因此,追随者的位置表示为:
(6)
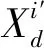
2 基于SSA算法的图像匹配
图像匹配过程中,有3个关键要素,分别是:特征提取、搜索策略和相似度量。在SSA算法图像匹配中,用HOG特征对待匹配图像进行特征提取,以SSA算法对待匹配图像进行搜索,并用相关系数函数进行相似度量。
在相似度量过程中,保留每次与目标相似度值最大的候选图像块,直至达到终止条件。此时与目标相似度值最大的候选图像块便是匹配目标。
2.1 特征提取
方向梯度直方图(histogram of oriented gradient,HOG)特征是通过计算和统计局部区域的梯度直方图来构成特征。它可以通过梯度或边缘的方向密度很好地描述图像中局部目标的表象和形状。HOG特征将目标位置和方向量化为梯度的幅值和方向,对图像的平移和旋转运动均具有适应性,并且对光照变化具有鲁棒性。文中选择HOG特征对目标图像块与样本图像块进行特征提取,像素点(x,y)处的梯度幅值和梯度方向分别为m(x,y),θ(x,y):
(7)
(8)
式中:Gx和Gy分别是水平方向和竖直方向梯度。
特征提取中,先根据式(7)和式(8)计算目标或样本图像块中每个像素的梯度幅值与方向,再将目标或样本图像块均匀地划分成多个单元细胞图像块(CELL),并且将梯度方向化为9个BIIN,分别统计其梯度方向直方图,得到CELL的HOG特征。将相邻的CELL组成一个BLOCK,将BLOCK进行归一化处理,得到BLOCK的HOG特征。
最后,统计BLOCK的梯度方向直方图,得到目标或样本图像块的HOG特征,此时便完成了特征提取。
2.2 相似度量
相似度量是为了测量目标图像块的HOG特征和候选图像块的HOG特征的相似程度。文中使用相关系数函数来度量两者之间的相似程度。设目标图像块的HOG特征用X表示,候选图像块的HOG特征用Y表示,则
式(9)表示两者的相关系数,其中:D(·)代表方差;cov(·)代表协方差;ρ(X,Y)代表相关系数。相关系数的值越大,两者的相似程度越大;反之,则两者的相似程度越小。
2.3 基于SSA算法的图像匹配
将图像匹配过程看作为一个组合优化问题,采用SSA优化策略完成图像匹配任务。
首先将待匹配图像看作是搜索空间,樽海鞘链中的领导者和追随者在搜索空间中移动,产生一系列初始候选图像块并提取特征;
然后计算候选图像块与目标图像块的相似度值,找出相似度值最大的图像块并保存,且此时的樽海鞘当作搜索空间中的食物;
根据式(2)和式(6)将樽海鞘链进行位置更新,从而产生新的候选图像块,计算出对应的相似度值,之后通过比较得到相似度最大的图像块并保存,同样的将此时的樽海鞘与当前食物的相似度值比较,保留其最大的并作为新的食物。
当达到最大迭代次数时,完成目标匹配。
基于SSA算法的图像匹配步骤如下:
初始化:待匹配图像的上界ub,下界lb;迭代次数lor 停止条件;目标图像T;利用式(1)初始化规模为N、维数为2的樽海鞘链群,由此产生N块候选图像块X(i) (i=1,2,3,…,N);
排序:fori=1:N
将群体中的樽海鞘按照R(i) 排序,相似度值大的一半视为领导者X1(j)(j=2,3,4,…,N/2),另一半视为追随者X2(k)(k=N/2+1,N/2+2,N/2+3,…,N)
end for
当前迭代次数l<最大迭代次数Lor 停止条件
fori=1:N
由式(2)得到X′1(j),由式(6)得到X′2(k),即得到X′(i),计算X′(i)与T的相似度R′(i) ;
ifR′(i)>FtthenFt′=R′(i) ;F′=F;
end if
end for
输出F′
3 实验与分析
实验运行环境为:Intel(R)Core(TM) i5-7300HQ CPU 2.5 GHz计算机;8GB内存;2G显卡;操作系统为64位windows10;软件平台为:Matlab R2017b。
实验中,选择粒子群优化算法(PSO)、蚁狮优化算法(ALO)以及文中SSA算法进行对比。
为了获得文中算法在实际图像的匹配效果,选择一幅大小为480像素×360像素的图像作为原始图像1,如图1(a);将原始图像1加入高斯噪声作为原始图像2,如图1(b);选取图中第170行,144列的点坐标作为模板图像的左上点,且模板图像大小为120像素×75像素,如图1(c)。

图1 原始图像
为了证明SSA在图像匹配过程中的鲁棒性和匹配效果,本实验采用原始图像2作为待匹配图像,如图2(a),分别使用3个优化算法进行100次实验。其中,种群规模设置为100,最大迭代次数为150。
本实验通过平均匹配时间、正确匹配次数和匹配成功率3个指标对实验结果进行评价。从匹配时间上看,SSA的匹配速度不是最快,但其匹配成功率和PSO一样高,并且匹配速度较ALO只差了1.2 s,这是由于本实验中所选参数并非是SSA的最优参数。

图2 匹配结果
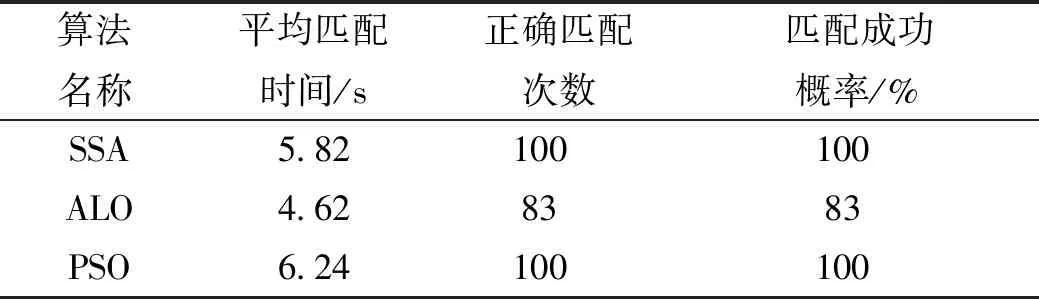
表1 不同算法匹配实验结果
SSA的快速匹配和高匹配精度得益于它特有的链式群更新模型。此模型中,追随者依靠前后彼此首尾相接的樽海鞘的位置实现位置更新,并非有强随机性,这使得樽海鞘链在搜索空间中搜索时很难错过最优位置以及陷入局部最优。并且个体的多样性大大加强了SSA的局部开发能力。而领导者在移动过程中会受到食物影响以及收敛因子作用,所以在全局探索和局部开发这两个状态转换中速度非常快,这大大加快了算法收敛速度,提高了SSA匹配速度以及匹配效果。
4 结论
针对传统群智能优化算法在图像匹配中调节参数多、匹配效果不理想问题,利用SSA算法链式群更新模型优势,平衡了优化算法在搜索过程中的全局探索和局部开发,提高了全局优化能力,避免了陷入局部最优。通过ALO和PSO以及SSA对比实验,实验结果验证了SSA算法在图像匹配中的匹配速度、匹配精度和鲁棒性。

