光雷多站测元数据极大似然实时交会算法*
罗成强,胡秋平,张 华 ,胡文华
(1 陆军工程大学石家庄校区,石家庄 050003;2 中国华阴兵器试验中心,陕西华阴 714200)
0 引言
常规兵器外弹道测量,常采用多台套光测(测元为A、E,A指方位角,E指俯仰角)、雷测(测元为R,指雷达距目标的距离)设备联合组网/接力、中心引导的测量模式,完成武器系统外弹道测试。在这种模式下,中心引导需要实时完成武器系统的外弹道参数解算,并为组网/接力测量设备提供引导数据,数据解算要求解算精度达到米级,实时性要求处理时间≤50 ms。针对光、雷多站测元数据实时处理算法,目前还没有统一的处理方式,一般根据具体任务采取相应的办法(如R-AE交会处理,多站最小二乘算法(NLSE))[1],上述算法一般受布站方式影响,存在较大的限制,如R-AE交会垂直角度盲区引起交会误差急剧增加、最小二乘迭代不收敛引起死循环使得解算时间长等,在数据故障的情况下需要人工挑选组网/接力测量设备或者切换其它计算方法,不能够完全满足武器装备外弹道测试实时性和测量精度要求。
对此,文中从概率角度出发提出一种基于距离估计的光电经纬仪-雷达多站测量数据极大似然交会算法,采用基于立体网格的模型实时求解方法,通过限定待求目标的空间坐标范围,使得目标以目标初值为中心,以3倍的交会精度为半径的保精度立体网格内,通过遍历法求出每个网格的似然函数值,似然函数值最大的网格点就是解算出的目标坐标,网格划分越小,定位精度越高。该方法避免了求解时间过长和可能发生的迭代死循环,仿真结果表明,目标坐标解算精度与多站最小二乘估计方法相当,6站交会情况下解算时间优于15 ms。
1 基于距离估计的光-雷多站测元数据交会算法(NMLE)
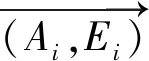
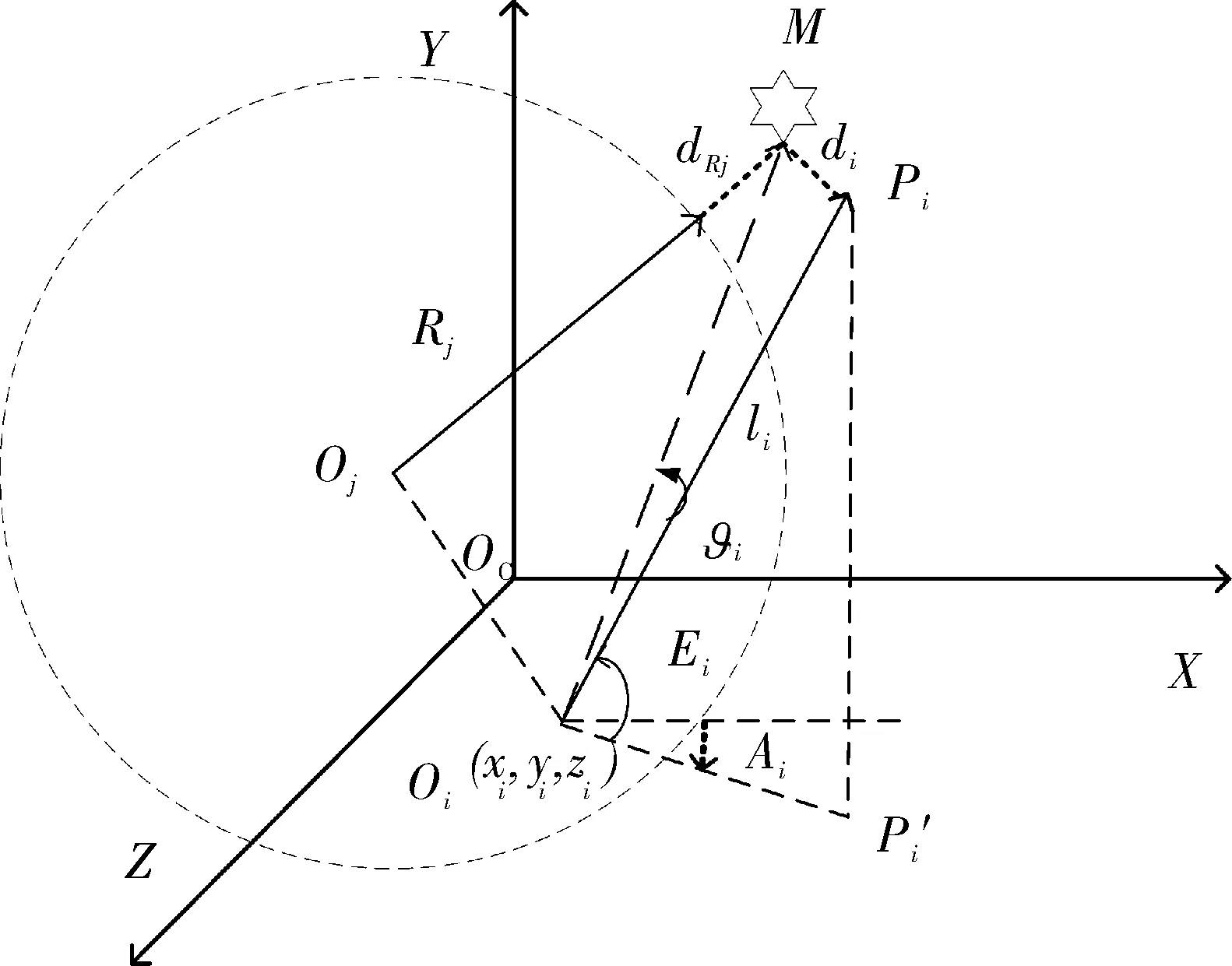
图1 设备观测示意图
(1)
(2)
其中:
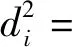
(x-xi)(z-zi)mihi+(y-yi)(z-zi)nihi),
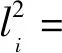
2((x-xi)(y-yi)mini+(x-xi)(z-zi)mihi+
(y-yi)(z-zi)nihi),
mi=cosAicosEi,ni=sinEi,hi=sinAicosEi。
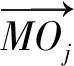
(3)
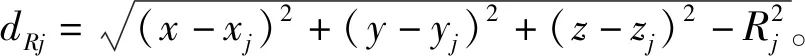
现有光测分站N台,雷测分站M台,则(N+M)台观测设备的多站似然函数为:
(4)
似然方程为:
(5)
根据极大似然原理,目标最有可能落在使似然方程极大的位置上,该位置即为目标的最优估计;即目标的最优估计模型为:
(6)
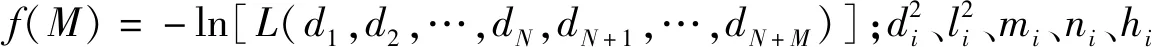
2 基于立体网格的模型实时求解
从式(6)可以看出,该模型为一无约束最优化求解问题,可以使用非线性无约束最优化解算方法进行解算迭代求解,要求初值(M0)要具有较好的精度值,使得迭代收敛较快,并且不易产生迭代死循环。理论上初值解算有两种情况:一是两站为光测站,则采用两站极大似然算法求解M0;二是两站为一台光测、一台雷达,则采用单站光雷算法(R-AE)[1]求解M0。但是从实时融合处理角度出发,为避免求解时间过长和可能发生的迭代死循环,采用通过限定待求目标的空间坐标范围,使得目标按照初值大概率位于以初值为中心,以交会精度为半径的保精度立体网格内,其中交会精度的给出根据初值求解算法精度按照实时系统的散布程度确定,这样处理后就把式(6)转化成有约束最优化问题,再通过遍历法相结合求解,求出每个网格的似然函数值,似然函数值最大的网格点就是解算出的目标坐标。
2.1 保精度立体网格的确定
保精度立体网格的确定采用优选方法,方法是先从多站光雷中确定初值,该初值应该是所有采用两站交会方法得出初值中精度最高的。初值确定后,根据相应的精度ε确定搜索网格半径长度为3ε。当中心引导系统在某一时刻接收到各测量站的测元数据时,若第i站和第j站为不同的测站,则可依据参考文献[1]计算其交会坐标M0和交会精度ε的值。
2.2 遍历法求解
采用“遍历法”求解式(6),遍历程序如下:
①接收多站测量数据,计算两两交会精度形成精度矩阵A。
②对精度矩阵A按照冒泡法排序得到精度最高测站精度ε。
③按照两站交会得到初始点M0及立体网格半径3ε。
④命k=0;定义遍历步长H。
⑤计算f(Mk;令P=f(Mk)。
⑥若(k+1)H<3ε,否则Mk即为所求M(x,y,z);计算f(Mk+H),若f(Mk+H)<|P|,P=f(Mk+H),进行⑦。
⑦命k=k+1,Mk+1=Mk+H;进行⑤。
3 算法分析
1)算法验证
假定待求目标为M(x,y,z),现有光测观测设备N=2台;现有雷测设备M=1台,称为测量分站O3,测元数据为R3。测元数据如下:
O1=(0,0,-1 000),σ1=0.005,(A1,E1)=(90.005,45);O2=(0,0,1 000),σ2=0.005,(A2,E2)=(270.005,45);O3=(0,0,0),σR3=1,R3=999。
选取初始点(0,0,999)及网格步长0.2;最终求得M为M(-0.087 2,1 000,0)。从结果可以看出,求解值M(-0.087 2,0,1 000)与真值M(0,1 000,0)误差小于0.1 m,计算结果是可信的。
2)仿真分析
为了评价算法是否满足实时性和解算精度要求,设计以下仿真方案:仿真生成测元数据,包括理论弹道、分站站址坐标、分站测角精度、分站测元数据(加入观测误差)。针对某时刻数据,首先进行两站(精度最高的两站)交会计算估计坐标参数M0,并计算交会精度值,同时确定网格大小和遍历步长;利用两站交会初始值,进行多站最小二乘估计和极大似然估计,估计空间坐标参数,计算交会精度值;通过增加分站数量,改变布站方式,检查有无无法求解的情况出现,最后统计NMLE算法的计算时间和处理精度。以某型火箭弹数据为例,理论弹道数据为帧频20 Hz,时间25 s,距离0~15 km。
仿真结果如下:
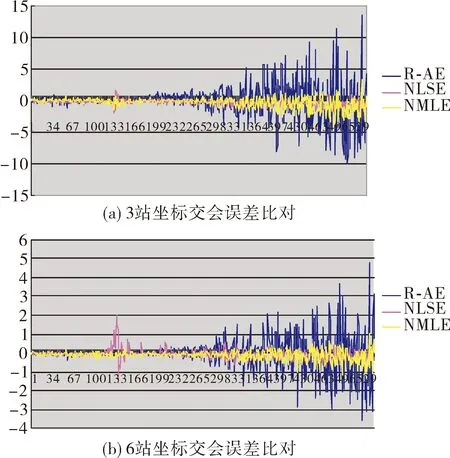
图2 3种交会方法弹道坐标处理误差比对

表1 NMLE极大似然算法数据处理结果表
从图2 3种交会方法弹道坐标处理误差比对可以看出,NMLE算法交会误差精度相比两站交会具有处理精度较高的优势,与NSLE算法相当,6测站交会结果相对3测站也具有处理精度高的特点。从表1结果看出,6站交会情况下,NMLE算法交会精度在15 km范围内优于3 m,处理时间优于15 ms。仿真结果表明,该算法实时处理时间、解算精度满足要求。
4 结束语
文中提出一种基于距离估计的多站光雷数据极大似然交会算法,面向中心引导实时处理系统对处理时间和精度的需求,建立了基于立体网格的数值解算求解方法,算法不涉及迭代处理,没有过基线、布站局限大、计算盲区等影响,通过对数值计算区域的限制(立体网格)解决了计算不收敛问题,满足实时数据处理的要求。仿真结果表明,目标坐标解算精度与多站最小二乘估计方法相当,6站交会情况下解算时间优于15 ms,坐标解算精度优于3 m,目前该算法已经成功应用于某型外弹道测量数据实时融合处理系统中。

