深海大区域目标落点声定位建模与仿真*

张 旭，张志伟

(91550部队，辽宁大连 116000)

0 引言

飞行器在海上入水时将产生一类识别度较高的击水声信号，该信号蕴含了入水目标的位置信息[1-2]，可用于进行无源定位。无源定位主要包括纯方位交会定位或时差定位，通常由多个水面或水下载体构成声基阵，根据入水声信号提取测量元素(到达时间或方位)，再进行交会解算[3-6]。纯方位交会定位误差随着测量区域的扩大而迅速增大[7]，不适用于深海大范围区域测量；而时差定位可利用入水声信号可识别度高、误差随距离变化慢的优势获得较好的深海测量特性[5]。现有入水目标无源定位大多应用在浅海，而在深海应用则面临着很多新的挑战：1)浅海测试中目标散布范围通常较小，典型测量海区尺度为O(1 km)[6]，而深海目标散布范围较大，典型测量海区尺度为O(10 km)，覆盖面积比浅海增加了100倍以上；2)浅海声场为波导传播，在较小测量区域通常可按常定声速梯度解算目标位置[4-5]，深海声场为会聚区声信道传播，声线修正问题不可忽略[8-9]；3)深海声传播距离较远，多途效应更加明显，使声基阵构型设计及信号处理方法变得复杂；4)在深远海开展测试水下空间先验信息少，不确定海洋环境将引起更大的测量误差。20世纪70-80年代，我国哈尔滨船舶工程学院曾在深海真实工况下成功开展入水目标的落点定位测量。但总体来看，入水目标的深海探测问题在理论和实践上的认识都很欠缺，相关机理性研究有待开展，需结合不断发展的水声定位技术和相关工程测试实践[10-12]探索新的方法和技术，为相关工程应用提供支撑。文中主要针对目标在深海大范围区域随机入水的工况，提出时差定位模型和Monte-Carlo仿真算法，通过精度仿真检验模型的有效性，并分析模型对于典型误差源的响应情况。

1 工况与环境条件

假设工况条件为：1)测量海区位于大洋中纬度海域(声速剖面如图1(a)所示)，测量范围为20 km×20 km，水深为5 200 m，海底平坦；2)待测目标以较高的速度入水，产生可识别的瞬态声信号；3)目标落点位置随机，在测量海区中心出现的概率较大，在测量海区边缘出现的概率较小，近似满足二维正态分布；4)以4个锚系潜标为基站，搭载接收器构成测量基阵，分别布放在测量海区的4个顶点，考虑到可利用会聚区声信道的可靠声路径获得较高信噪比，将各基站布放在水下4 000 m深处。

图1(b)为目标入水声信号随距离和深度的传播损失图，传播损失由BELLHOP高斯束射线模型[13]计算，垂直和水平方向的网格分辨率分别取5 m和50 m，接收器中心频率为1 kHz；掠射角范围取0°～90°，掠射角间隔设为0.18°。由图可见，声场呈现会聚区声信道样式，在30 km处约为1/2个会聚区距离，最初数公里范围的声能近似按球面扩展向海底辐射。而10 km之外的声场能量主要沿3 500 m以下的反转声线传播，靠近海底的声能明显高于上层海洋。假设目标入水声信号在1 kHz的谱级不小于200 dB，环境噪声和接收器噪声的谱级不超过90 dB，根据声呐方程估算，测量海区内的接收器可获得超过10 dB的信噪比。尽管声信号可沿多路径到达，但沿直达声波的到达时延最短、能量最强，可作为主要的测量信息。对于上述工况，布放在4 000 m处的接收器在测量范围内均位于声影区外，有对应的直达声波。

2 声定位模型

2.1 模型建立

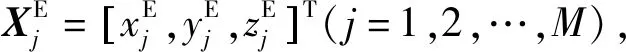
(1)

式中:‖·‖2表示向量的l2范数。

若考虑将目标声信号沿弯曲路径传播到接收器的过程等效为沿某一等效声速直线传播，且目标入水的时间为零时刻，则有Rj=CjTj，其中Cj为等效声速，Tj为到达时延。对式(1)在某一初始位置X0=[x0，y0，z0]T进行泰勒级数展开：

(2)

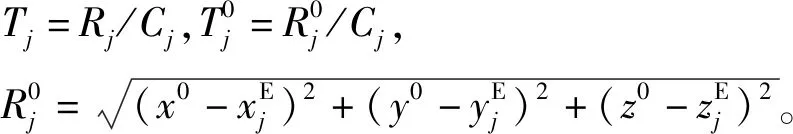
图1 海区声速剖面及传播损失示意图

由于测量信息为特征声信号到达各基站时间的估计值，而目标实际入水时未知，因此测量元素为目标声信号到达各基站的时间差，即：

(3)

将上式写成矩阵形式的表达式为：

ΔT=AΔX

(4)

其中：

式中:j=1，2，…，N-1；k=2，3，…，N，j≠k。

根据高斯-马尔可夫理论，可由非线性最小二乘法得出目标参数的估计值：

(5)

2.2 声速修正

(6)

式中c(z)为声速剖面函数。

根据前文假设，可将声信号沿直达本征声线(非常定声速梯度条件下通常为不规则曲线)传播等效为以某一等效声速沿从待测目标到基站的直线传播，两者经历时延相等，则该等效声速可表示为：

(7)

图2给出了5 km、15 km和25 km 3个接收点的直达本征声线，声线从不同目标位置到达不同接收器的路径弯曲程度各不相同，所经历的时延也不同。本征声线作为联系海洋声速环境与定位解算的重要参量，携带了目标声信号在非定常声速环境下的到达时延信息，并通过等效声速参量传递到测量方程。

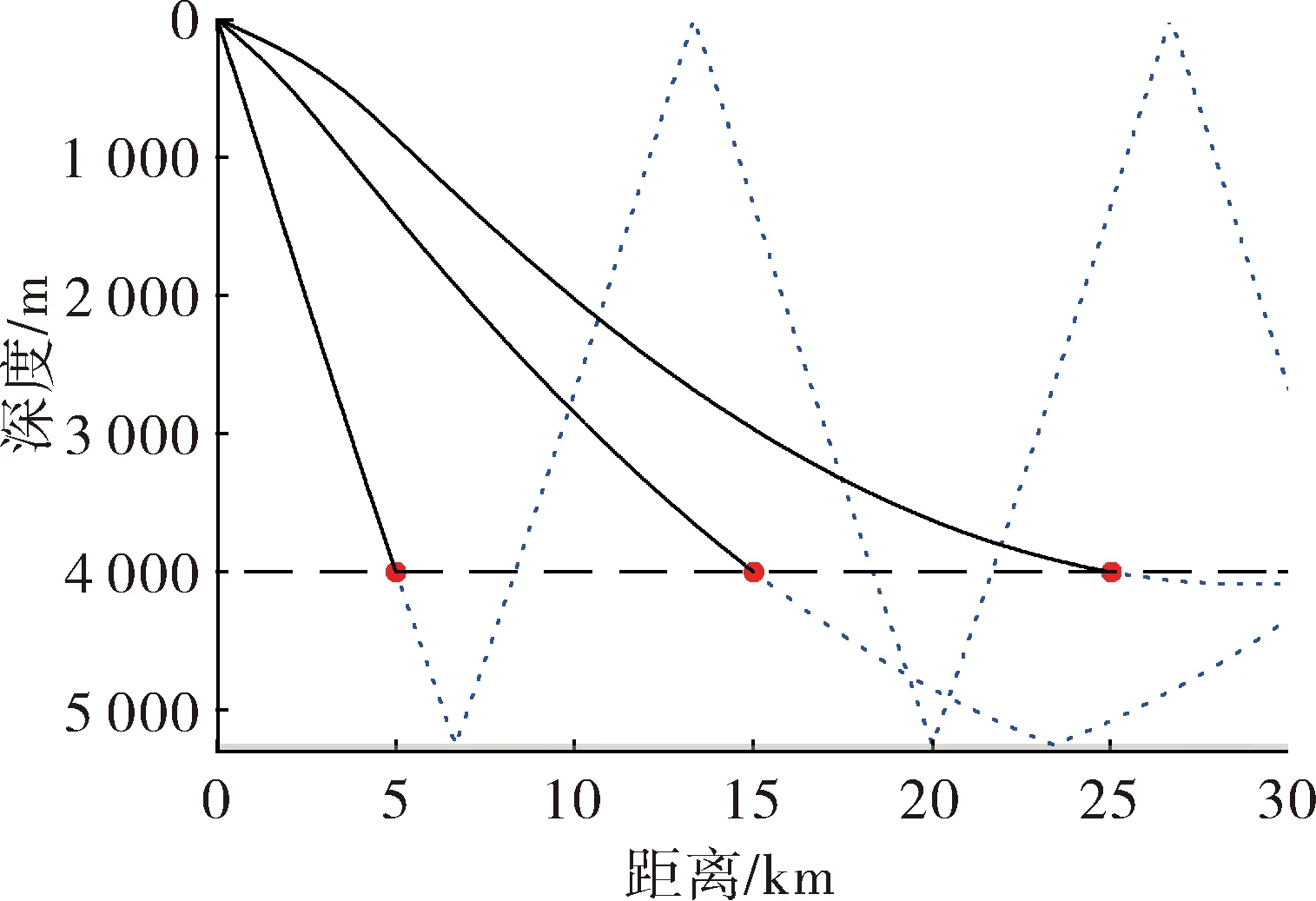
图2 直达本征声线传播示意图(接收器分别位于5 km、15 km、25 km的4 000 m深处，声线到达前由实线表示，到达后由虚线表示)

2.3 收敛性分析

定位模型解算属于超定方程组的最小二乘求解问题，文献[14]已针对此类方程的收敛性进行了详细推导，证明了其目标函数二阶项相对于一阶项是小量，近似满足局部线性收敛。图3给出了一次抽样解算过程中的收敛性示意图，图3(a)为目标函数在XOY面的分布，可见目标函数在极小值附近均有较好的连续性；图3(b)为箱型图显示的1 000组抽样解算后的定位偏差随迭代次数的变化，箱型中心表示0.5分位数，箱型边界分别表示0.25和0.75分位数，可以看出迭代过程收敛速度很快，通常3～5步即可达到极小点。

3 精度仿真分析

3.1 误差源设置

1)基站站址误差(δE)：各基站位置坐标的标定误差。考虑利用典型水声定位设备对基站标定的位置精度可达到0.2%～0.3%斜距[15-16]，对于上述测量海区X方向标准差σEx和Y方向标准差σEy可设为20 m；基站深度信息可由搭载的深度-压力传感器提供，Z方向标准差σEz可设为2 m。

2)时延误差(δτ)：由测量海区声速起伏引起的时延到达误差和由信号序列提取到达时刻估计误差组成。根据实测数据统计，可将海域声速标准差σc设为3 m/s；在较高信噪比条件下，时延估计精度通常优于毫秒级[17]，远小于声速起伏引起的误差。根据工程经验，将总的时延误差标准差στ设为50 ms。

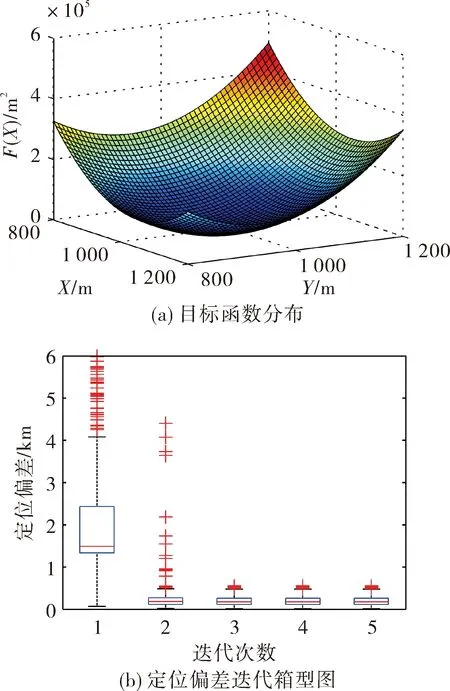
图3 迭代解算收敛性示意图

3)基站守时误差(δt)：基站布设后的守时误差。考虑各基站完成时间同步后布放，12 h内完成测试回收，按现有设备守时稳定度估计，时间漂移误差小于1 μs，相对于时延误差可忽略。

3.2 仿真算法

采用Monte-Carlo方法设计仿真算法[18]，仿真流程如下：

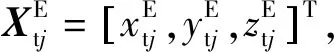
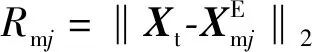
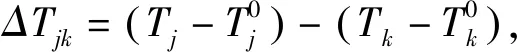
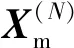
3.3 仿真结果分析

图4给出了等时差二次曲线交会定位示意图，基阵构型为四元阵，基线长度为20 km，各基站布设于4 000 m水深，落点位置真值设为(1，1)，图中标示了真值、测量值和初始值的位置。在图4(a)中，基站位置和时间差代入误差源，二次曲线不完全交会，收敛点有明显偏差，测量值反映的是多组测量数据“相互妥协”后的最小二乘估计结果；在图4(b)中，基站位置和时间差代入真值，各曲线交会于一点，测量值与真值完全吻合，说明不代入误差源时，收敛点无偏差，从而验证了模型的合理性。

图4 二次曲线交会定位示意图(+表示真值位置， x表示测量值位置，*表示初始值位置)

以下分两种情况考察测量模型对于目标落点位置和基阵构型变化的响应。

1)目标位置变化

对于基线长度为20 km的四元阵，考虑目标落点位置分别位于阵中心(0，0)、X轴上的(0，5)和(0，8)、Y轴上的(5，0)和(8，0)、对角线上的(5，5)和(8，8)等情况见图5(a)，仿真结果见图5(b)～图5(d)和表1。当目标位于阵中心或对角线上时，X与Y方向的RMSE较对称，定位误差随着目标靠近基阵顶角而增大，在(8，8)处RMSE相对于(0，0)处增加了约30 m。当目标落点位于X轴时，X方向的定位性能变差，目标位置从(0，0)变化到(8，0)，X方向RMSE增加了约40 m，而Y方向RMSE没有显著增大。这是因为随着X方向距离增大，沿平行于X方向的二次曲线被拉长，交会点的不确定度增加，因此交会性能变差；当目标位于Y轴上时情况正好相反。

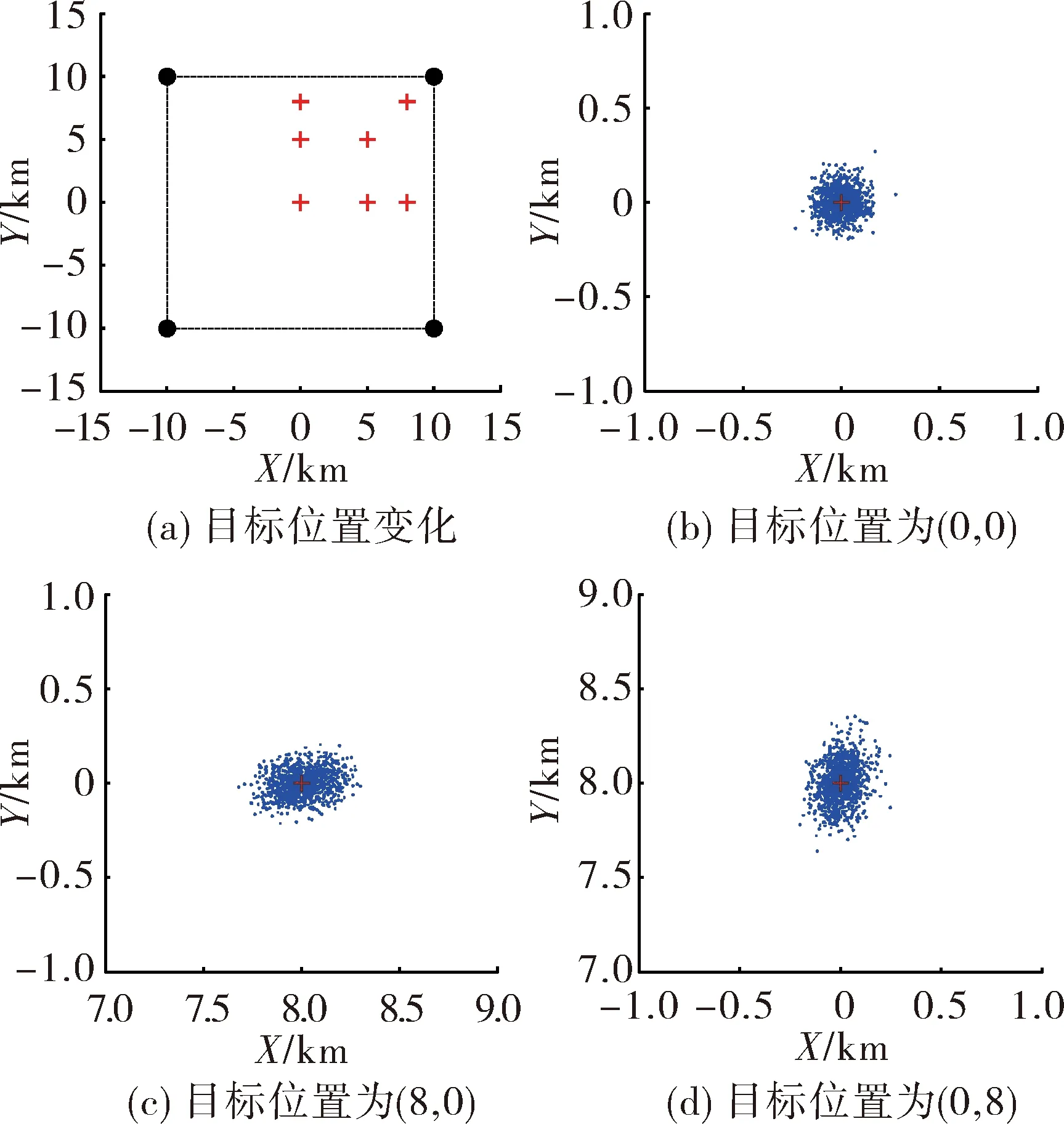
图5 不同目标位置定位结果分布图(图(a)中圆点表示基站位置，+表示目标位置)

2)基站构型变化

参照基线长度为20 km的四元阵、目标落点位于基阵几何中心的情况，考虑基阵旋转45°、X方向基线长度加长10 km(Y方向不变)、Y方向基线长度加长10 km(X方向不变)3类条件变化(见图6(a))，仿真结果见图6(b)～图6(d)和表2。与前文结果比较，在不改变基本构型的情况下，基阵旋转对于定位精度的改进不明显，说明定位精度与坐标系选取无关。当X方向基线增加时，X方向定位精度有所提升，而Y方向定位精度明显变差，两个方向的变化不对称，X方向基线长度由20 km增加到30 km，X方向定位精度略提升了数米，而Y方向定位精度下降了约30 m；反之，当Y方向基线增大时，Y方向定位精度提升，X方向精度下降。

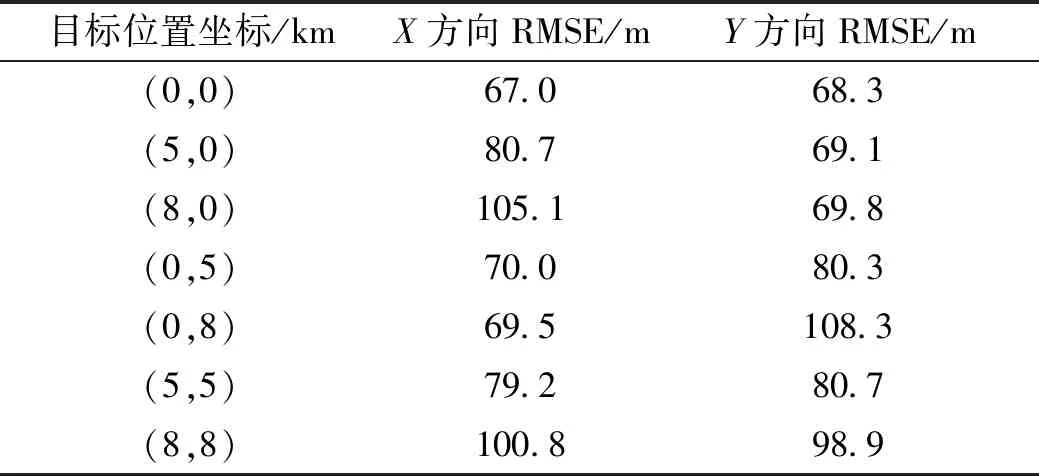
表1 同目标落点位置定位结果比较

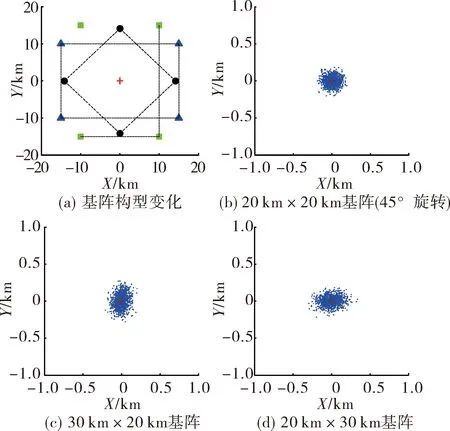
图6 不同基站构型定位结果分布图(图(a)中圆点、三角形、正方形表示基站位置，+表示目标位置)

4 结论

对于在深海大区域随机入水的飞行目标，为获取其入水点位置坐标，可利用目标击水声信号对其进行无源定位。文中针对此类工况建立了一种基于入水声信号到达时间差的定位模型，并提出了Monte-Carlo精度仿真算法。在接收基阵为四元阵和典型误差源条件下，目标位于基阵中心位置时X方向和Y方向的RMSE为67.0 m、68.3 m，位于沿X轴靠近基阵边缘位置时RMSE为105.1 m、69.8 m，位于沿Y轴靠近基阵边缘位置时RMSE为69.5 m、108.3 m，位于靠近基阵顶角位置时RMSE为100.8 m、98.9 m。仿真结果表明，测量模型能够对目标位置和基阵构型变化产生合理的响应，进而验证了模型的正确性和可靠性，可为测量系统的论证设计提供方法。

在深海条件下考虑目标落点的定位测量，面临很多新问题和挑战。文中仅讨论了典型四元阵条件下利用深海会聚区声信道的可靠声路径进行定位的情况，但并未讨论复杂基阵构型以及其它类型声信道的定位性能，也未考虑多途信息应用、非均匀水下环境影响等问题，更复杂工况下的机理性研究有待进一步开展。